
6.若随机变量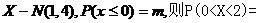 ( )
( )
A.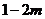 B.
B.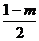
C.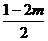 D.
D.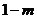
5.某农科院在3×3的9块式验田中选出6块种植某品种水稻进行试验,则每行每列都有一块试验田种植水稻的概率为 ( )
A.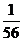 B.
B.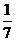
C.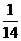 D.
D.
4.已知双曲线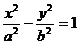 ,F1是左焦点,O是坐标原点,若双曲线上存在点P,使
,F1是左焦点,O是坐标原点,若双曲线上存在点P,使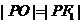 ,则此双曲线的离心率的取值范围是 ( )
,则此双曲线的离心率的取值范围是 ( )
A.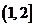 B.
B.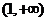 C.(1,3) D.
C.(1,3) D.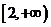
3.已知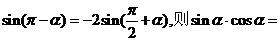 ( )
( )
A.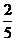 B.
B.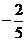 C.
C.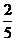 或
或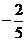 D.
D.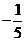
2.已知复数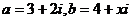 (其中
(其中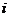 为虚数单位),若复数
为虚数单位),若复数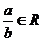 ,则实数
,则实数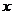 的值为
的值为
( )
A.-6 B.6 C.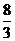 D.-
D.-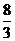
1.已知集合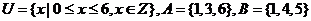 ,则
,则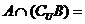 ( )
( )
A.{1} B.{3,6} C.{4,5} D.{1,3,4,5,6}
21.(本小题满分13分)
已知焦点在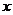 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为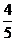 ,且过点
,且过点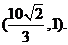
(1)求椭圆C的方程;
(2)直线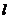 分别切椭圆C与圆
分别切椭圆C与圆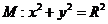 (其中
(其中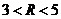 )于A、B两点,求|AB|的最大值。
)于A、B两点,求|AB|的最大值。
20.(本小题满分13分)
各项均不为零的数列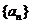 ,首项
,首项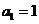 ,且对于任意
,且对于任意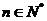 均有
均有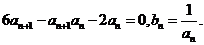
(1)求数列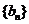 的通项公式;
的通项公式;
(2)数列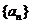 的前
的前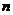 项和为
项和为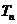
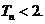
19.(本小题满分13分)
某电视生产厂家有A、B两种型号的电视机参加家电下乡活动。若厂家投放A、B型号电视机的价值分别为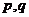 万元,农民购买电视机获得的补贴分别为
万元,农民购买电视机获得的补贴分别为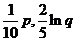 万元。已知厂家把总价值为10万元的A、B两种型号电视机投放市场,且A、B两型号的电视机投放金额都不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值(精确到
万元。已知厂家把总价值为10万元的A、B两种型号电视机投放市场,且A、B两型号的电视机投放金额都不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值(精确到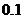 ,参考数据:
,参考数据: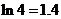 )
)
18.(本小题满分12分)
如图,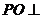 平面ABCD,点O在AB上,EA//PO,四边形ABCD为直角梯形,BC
平面ABCD,点O在AB上,EA//PO,四边形ABCD为直角梯形,BC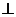 AB,BC=CD=BO=PO,
AB,BC=CD=BO=PO,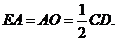
(1)求证:BC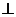 平面ABPE;
平面ABPE;
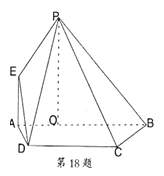 (2)直线PE上是否存在点M,使DM//平面PBC,若存在,求出点M;若不存在,说明理由。
(2)直线PE上是否存在点M,使DM//平面PBC,若存在,求出点M;若不存在,说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com