
9.汽车以10 m/s的速度行驶5分钟后突然刹车.如刹车过程是做匀变速运动,加速度大小为5m/s2 ,则刹车后3秒钟内汽车所走的距离是____________.
8.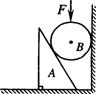 如图所示,横截面为直角三角形斜劈A,放在粗糙的水平地面上,在劈与竖直墙壁之间放置一光滑球B,系统处于静止状态.在球B上施一通过球心的力F,系统仍保持静止,下列说法正确的是
如图所示,横截面为直角三角形斜劈A,放在粗糙的水平地面上,在劈与竖直墙壁之间放置一光滑球B,系统处于静止状态.在球B上施一通过球心的力F,系统仍保持静止,下列说法正确的是
A.B所受合外力增大
B.B对竖直墙壁的压力增大
C.地面对A的摩擦力减小
D.A对地面的摩擦力将小于B对墙壁的压力
7.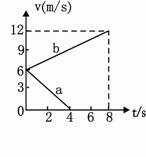 质量为0.8kg的物体在一水平面上运动,如图所示的两
质量为0.8kg的物体在一水平面上运动,如图所示的两
条直线分别表示物体受到水平拉力和不受水平拉力作用
时的v-t图线,g取10m/s2,下列判断正确的是
A.a是物体受到水平拉力作用时的v-t图线
B.b是物体受到水平拉力作用时的v-t图线
C.物体与地面的动摩擦因数为0.15
D.物体受到的水平拉力为0.6N
6.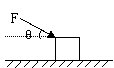 如图所示,水平面上,质量为m的物块受到与水平方向夹角
如图所示,水平面上,质量为m的物块受到与水平方向夹角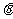 的推力F的作用(
的推力F的作用(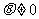 ),物块做匀速直线运动.现将F撤去,设此后物块运动过程中加速度的大小为
),物块做匀速直线运动.现将F撤去,设此后物块运动过程中加速度的大小为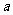 ,则
,则
A.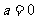 B.
B.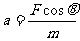
C.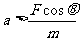 D.
D.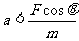
5.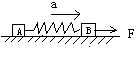 如图所示,光滑水平面上物体A和B以轻弹簧相连接,在水平拉力F作用下,以加速度a做直线运动,设A和B的质量分别为mA和mB,当突然撤掉力F时,A和B的加速度分别为:
如图所示,光滑水平面上物体A和B以轻弹簧相连接,在水平拉力F作用下,以加速度a做直线运动,设A和B的质量分别为mA和mB,当突然撤掉力F时,A和B的加速度分别为:
A.0,0; B.a,0;
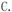 mAa/(mA+mB),mAa/(mA+mB); D.a,-mAa/mB
mAa/(mA+mB),mAa/(mA+mB); D.a,-mAa/mB
4.在一竖直砖墙前让一个小石子自由下落,小石子下落的轨迹距离砖墙很近. 现用照相机对下落的石子进行拍摄.某次拍摄的照片如图所示,AB为小石子在这次曝光中留下的模糊影迹.已知每层砖(包括砖缝)的平均厚度约为 6cm,A点距石子开始下落点的竖直距离约1.8m.估算照相机这次拍摄的“曝光时间”最接近
A.2.0×10-1s B.2.0×10-2s
C.2.0×10-3s D.2.0×10-4s
3.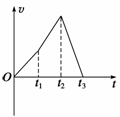 一枚火箭由地面竖直向上发射,其速度和时间的关系图线如图
一枚火箭由地面竖直向上发射,其速度和时间的关系图线如图
所示,则
A.t3时刻火箭距地面最远
B.t2-t3的时间内,火箭在向下降落
C.t1-t2的时间内,火箭处于失重状态
 D.0-t3的时间内,火箭始终处于失重状态
D.0-t3的时间内,火箭始终处于失重状态
2.如图所示,一木块放在水平桌面上,在水平方向上共受三
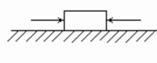 个力,F1,F2和摩擦力,处于静止状态.其中F1=10N,F2=2N.
个力,F1,F2和摩擦力,处于静止状态.其中F1=10N,F2=2N.
若撤去力F1则木块在水平方向受到的合外力为
A.10N向左 B.6N向右
C.2N向左 D.0
1.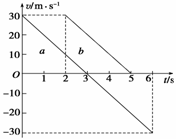 如图所示,a、b分别表示先后从同一地点以相同的初
如图所示,a、b分别表示先后从同一地点以相同的初
速度做匀变速直线运动的两个物体的速度图象,则下
列说法正确的是
A.4s末两物体的速度相等
B.4s末两物体在途中相遇
C.5s末两物体的速率相等
D.5s末两物体相遇
(17)(本小题满分10分)
在关于人体脂肪含量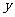 (百分比)和年龄
(百分比)和年龄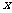 关系的研究中,得到如下一组数据
关系的研究中,得到如下一组数据
年 龄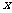 |
23 |
27 |
39 |
41 |
45 |
50 |
脂肪含量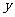 |
9.5 |
17.8 |
21.2 |
25.9 |
27.5 |
28.2 |
 (Ⅰ)画出散点图,判断x与y是否具有相关关系;
(Ⅰ)画出散点图,判断x与y是否具有相关关系;
(Ⅱ)通过计算可知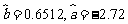 ,请写出y对x的回归直线方程,并计算出
,请写出y对x的回归直线方程,并计算出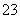 岁和
岁和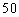 岁的随机误差.
岁的随机误差.
(18)(本小题满分12分)
已知函数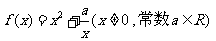 .
.
(Ⅰ)讨论函数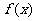 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(Ⅱ)若函数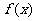 在
在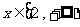 上为增函数,求
上为增函数,求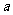 的取值范围.
的取值范围.
(19)(本小题满分12分)
某体育训练队共有40人,下表为跳高、跳远成绩的人数分布表,成绩分为1-5个档次,例如表中所示跳高成绩为4分、跳远成绩为2分的队员为5人,将全部队员的姓名卡混合在一起,任取一张,设该队员的跳高成绩为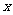 ,跳远成绩为
,跳远成绩为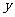 ,设
,设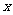 ,
,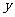 为随机变量(注:没有相同姓名的队员).
为随机变量(注:没有相同姓名的队员).
 跳远成绩y 跳远成绩y跳高成绩x
|
5 |
4 |
3 |
2 |
1 |
||
|
5 |
1 |
3 |
1 |
0 |
1 |
||
|
4 |
1 |
0 |
2 |
5 |
1 |
||
|
3 |
2 |
1 |
0 |
4 |
3 |
||
|
2 |
1 |
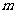 |
6 |
0 |
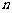 |
||
|
1 |
0 |
0 |
1 |
1 |
3 |
(Ⅰ)求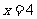 的概率及
的概率及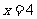 且
且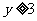 的概率;
的概率;
(Ⅱ)若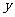 的数学期望为
的数学期望为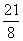 ,求
,求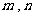 的值.
的值.
(20)(本小题满分20分)
为迎接上海世博会,某旅游部门开发了一种新产品,每件产品的成本是15元,销售价是20元,月平均销售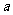 件.通过改进工艺,产品的成本不变,质量和技术含量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含量提高,市场分析的结果表明,如果产品的销售价提高的百分率为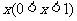 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为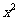 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是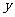 (元).
(元).
(Ⅰ)写出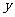 关于
关于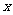 的函数关系式;
的函数关系式;
(Ⅱ)改进工艺后,确定该纪念品的售价,使得旅游部门销售该纪念品的月平均利润最大.
(21)(本小题满分12分)
设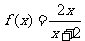 ,
,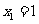 ,
,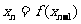
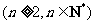 .
.
(Ⅰ)求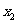 ,
,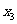 ,
,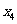 的值;
的值;
(Ⅱ)归纳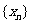 的通项公式,并用数学归纳法证明.
的通项公式,并用数学归纳法证明.
(22)(本小题满分12分)
已知函数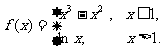
(Ⅰ)求函数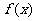 的单调减区间;
的单调减区间;
(Ⅱ)若不等式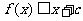 对一切x∈R恒成立,求
对一切x∈R恒成立,求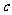 的取值范围.
的取值范围.
|

|
版权所有:()
2009-2010学年度第二学期期末考试
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com