
32. (2010银川一中二模)以下文字通过比喻揭示了各种人对人生的不同认识,请再补写三句。
要求:①从反面写,和前面正确的人生观构成对比关系;②句式基本一致;③字数不要求完全相同。
希望说,人生就是万绿之源的绚丽的花朵。
成功说,人生就是建筑历史的一块砖石。
奋斗说,人生就是与风浪搏斗的一叶扁舟。
___________________________________________________________ ___
___________________________________________________________ ___
___________________________________________________________ ___
___________________________________________________________ ___
___________________________________________________________ ___
___________________________________________________________ ___
31. (2010浙江菱湖中学二模)时事评论:北京大学业2010年自主招生,试点推出“中学校长实名推荐制”,全国39所中学的校长获得推荐资格,被推荐的学生可被北大降30分录取。此举引发了社会广泛的关注和争议。对北大试行“中学校长实名推荐制”一事,你赞成还是反对?请谈谈你的看法,并简述理由。不少于80字。
___________________________________________________________ ___
___________________________________________________________ ___
___________________________________________________________ ___
___________________________________________________________ ___
___________________________________________________________ ___
30.(2010浙江菱湖中学二模)下面是《宽心谣》的前几句,分别以“时间\处事\金钱”为表述的对象。请你模仿歌谣的句式,以“吃”“穿”或生活的其他方面作为表述对象,再续编两句歌谣,注意:(1)内容的相对和谐,(2)语言风格的基本统一。
宽心谣
日出东海落西山,愁也一天,喜也一天。
遇事不钻牛角尖,人也舒坦,心也舒坦。
每月领取养老钱,金也喜欢,少也喜欢。
4.已知函数f(x)=asin2x+cos2x(a∈R)图象的一条对称轴方程为x=,则a的值为________.
解析:∵x=是对称轴,∴f(0)=f(),即cos0=asin+cos,∴a=.
3.(2009年高考江西卷改编)若函数f(x)=(1+tanx)cosx,0≤x<,则f(x)的最大值为________.
解析:f(x)=(1+·)·cosx=cosx+sinx=2sin(x+),
∵0≤x<,∴≤x+<,∴当x+=时,f(x)取得最大值2.答案:2
2.(2009年高考广东卷改编)函数y=2cos2(x-)-1是________.
①最小正周期为π的奇函数 ②最小正周期为π的偶函数 ③最小正周期为的奇函数 ④最小正周期为的偶函数
解析:y=2cos2(x-)-1=cos(2x-)=sin2x,∴T=π,且为奇函数.
答案:①
1.(2009年高考四川卷改编)已知函数f(x)=sin(x-)(x∈R),下面结论错误的是.
①函数f(x)的最小正周期为2π②函数f(x)在区间[0,]上是增函数
③函数f(x)的图象关于直线x=0对称④函数f(x)是奇函数
解析:∵y=sin(x-)=-cosx,y=-cosx为偶函数,
∴T=2π,在[0,]上是增函数,图象关于y轴对称.答案:④
8.设双曲线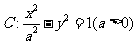 与直线
与直线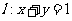 相交于两个不同的点
相交于两个不同的点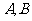 .
.
(1)求双曲线的离心率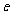 的取值范围;(2)设直线
的取值范围;(2)设直线 与
与 轴的交点为
轴的交点为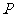 ,且
,且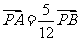 ,求
,求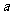 的值.
的值.
7.已知某椭圆的焦点是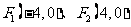 ,过点
,过点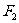 并垂直于
并垂直于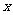 轴的直线与椭圆的一个交点为
轴的直线与椭圆的一个交点为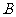 ,且
,且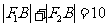 .椭圆上不同的两点
.椭圆上不同的两点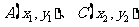 满足条件:
满足条件: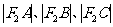 成等差数列.
成等差数列.
(Ⅰ)求该椭圆的方程;(Ⅱ)求弦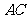 中点的横坐标;
中点的横坐标;
(Ⅲ)设弦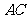 垂直平分线的方程为
垂直平分线的方程为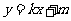 ,求
,求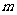 的取值范围.
的取值范围.
6.设抛物线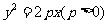 ,
, 内接于抛物线,
内接于抛物线,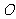 为坐标原点,
为坐标原点,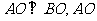 所在的直线方程为
所在的直线方程为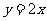 ,
,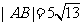 ,求抛物线方程.
,求抛物线方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com