
2.气体的体积主要由以下什么因素决定的:①气体分子的直径 ②气体物质的量的多少?③气体分子间的平均距离 ④气体分子的相对分子质量 ( )
A.①② B.①③
C.②③ D.②④
1.我国的“神州五号”载人飞船已发射成功,“嫦娥”探月工程已正式启动。据科学家预测,月球的土壤中吸附着数百万吨的32He,每百吨32He核聚变所释放出的能量相当于目前人类一年消耗的能量。在地球上,氦元素主要以42He的形式存在。下列说法正确的是: ( )
A.42He原子核内含有4个质子
B.32He和42He互为同位素
C.32He原子核内含有3个中子
D.42He的最外层电子数为2,所以42He具有较强的金属性
15. (2008·广东五校联考)在△ABC中,角A、B、C的对边分别为a、b、c,已知a+b=5,c=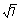 ,且4sin2
,且4sin2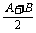 -cos2C=
-cos2C=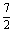 .
.
(1)求角C的大小;(2)求△ABC的面积.
解 (1)∵A+B+C=180°,由4sin2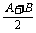 -cos2C=
-cos2C=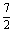 ,得4cos2
,得4cos2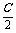 -cos2C=
-cos2C=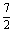 ,
,
∴4·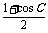 -(2cos2C-1)=
-(2cos2C-1)=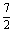 ,整理,得4cos2C-4cosC+1=0,解得cosC=
,整理,得4cos2C-4cosC+1=0,解得cosC=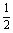 ,
,
∵0°<C<180°,∴C=60°.
(2)由余弦定理得c2=a2+b2-2abcosC,即7=a2+b2-ab,∴7=(a+b)2-3ab,
由条件a+b=5,得7=25-3ab,ab=6,∴S△ABC=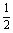 absinC=
absinC=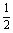 ×6×
×6×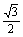 =
=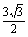 .
.
14. 已知△ABC的三个内角A、B、C的对边分别为a、b、c,若a、b、c成等差数列,且2cos2B-8cosB+5=0,求角B的大小并判断△ABC的形状.
解 方法一 ∵2cos2B-8cosB+5=0,∴2(2cos2B-1)-8cosB+5=0.
∴4cos2B-8cosB+3=0, 即(2cosB-1)(2cosB-3)=0.
解得cosB=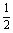 或cosB=
或cosB=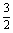 (舍去).∴cosB=
(舍去).∴cosB=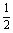 .∵0<B<
.∵0<B<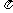 ,∴B=
,∴B=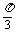 .
.
∵a,b,c成等差数列,∴a+c=2b.∴cosB= =
=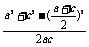 =
=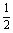 ,
,
化简得a2+c2-2ac=0,解得a=c.又∵B=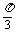 ,∴△ABC是等边三角形.
,∴△ABC是等边三角形.
方法二 ∵2cos2B-8cosB+5=0,∴2(2cos2B-1)-8cosB+5=0.
∴4cos2B-8cosB+3=0,即(2cosB-1)(2cosB-3)=0.
解得cosB=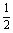 或cosB=
或cosB=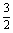 (舍去).∴cosB=
(舍去).∴cosB=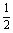 ,∵0<B<
,∵0<B<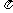 ,∴B=
,∴B=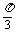 ,
,
∵a,b,c成等差数列,∴a+c=2b.由正弦定理得sinA+sinC=2sinB=2sin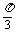 =
=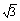 .
.
∴sinA+sin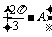 =
=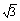 ,∴sinA+sin
,∴sinA+sin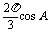 -cos
-cos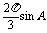 =
=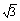 .
.
化简得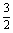 sinA+
sinA+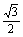 cosA=
cosA=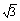 ,∴sin
,∴sin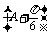 =1.
=1.
∴A+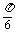 =
= ,∴A=
,∴A=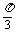 ,∴C=
,∴C=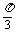 ,∴△ABC为等边三角形.
,∴△ABC为等边三角形.
13. 已知△ABC中,三个内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且2S=(a+b)2-c2,求tanC的值.
解 依题意得absinC=a2+b2-c2+2ab,由余弦定理知,a2+b2-c2=2abcosC.
所以,absinC=2ab(1+cosC),即sinC=2+2cosC,所以2sin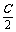 cos
cos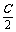 =4cos2
=4cos2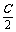
化简得:tan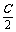 =2.从而tanC=
=2.从而tanC=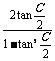 =-
=-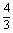 .
.
12. 在△ABC中,a、b、c分别表示三个内角A、B、C的对边,如果(a2+b2)sin(A-B)=(a2-b2)sin(A+B),判断三角形的形状.
解 方法一 已知等式可化为a2[sin(A-B)-sin(A+B)]=b2[-sin(A+B)-sin(A-B)]∴2a2cosAsinB=2b2cosBsinA
由正弦定理可知上式可化为:sin2AcosAsinB=sin2BcosBsinA
∴sinAsinB(sinAcosA-sinBcosB)=0∴sin2A=sin2B,由0<2A,2B<2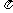
得2A=2B或2A=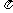 -2B,即A=B或A=
-2B,即A=B或A=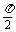 -B,∴△ABC为等腰或直角三角形.
-B,∴△ABC为等腰或直角三角形.
方法二 同方法一可得2a2cosAsinB=2b2sinAcosB
由正、余弦定理,可得a2b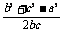 = b2a
= b2a ∴a2(b2+c2-a2)=b2(a2+c2-b2)
∴a2(b2+c2-a2)=b2(a2+c2-b2)
即(a2-b2)(a2+b2-c2)=0∴a=b或a2+b2=c2∴△ABC为等腰或直角三角形.
11. 在△ABC中,a、b、c分别是角A,B,C的对边,且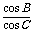 =-
=-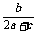 .
.
(1)求角B的大小;(2)若b=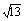 ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
解 (1)由余弦定理知:cosB= ,cosC=
,cosC= .
.
将上式代入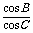 =-
=-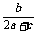 得:
得: ·
·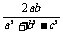 =-
=-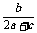
整理得:a2+c2-b2=-ac∴cosB= =
=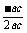 =-
=-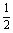
∵B为三角形的内角,∴B=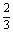
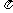 .
.
(2)将b=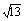 ,a+c=4,B=
,a+c=4,B=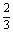
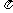 代入b2=a2+c2-2accosB,得b2=(a+c)2-2ac-2accosB
代入b2=a2+c2-2accosB,得b2=(a+c)2-2ac-2accosB
∴b2=16-2ac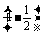 ,∴ac=3.∴S△ABC=
,∴ac=3.∴S△ABC=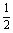 acsinB=
acsinB=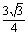 .
.
10. 在△ABC中,已知a=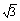 ,b=
,b= ,B=45°,求A、C和c.
,B=45°,求A、C和c.
解 ∵B=45°<90°且asinB<b<a,∴△ABC有两解.
由正弦定理得sinA=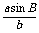 =
=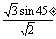 =
=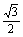 ,
,
则A为60°或120°.
①当A=60°时,C=180°-(A+B)=75°,
c=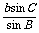 =
=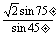 =
=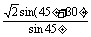 =
=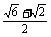 .
.
②当A=120°时,C=180°-(A+B)=15°,
c=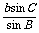 =
=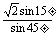 =
=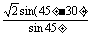 =
=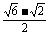 .
.
故在△ABC中,A=60°,C=75°,c=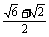 或A=120°,C=15°,c=
或A=120°,C=15°,c=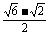 .
.
9.在△ABC中,角A、B、C所对的边分别为a、b、c.若(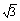 b-c)cosA=acosC,则cosA=
.
b-c)cosA=acosC,则cosA=
.
答案 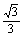
B组
8. 在△ABC中,A=60°,AB=5,BC=7,则△ABC的面积为 .
答案 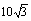
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com