
7.(重庆卷理15)已知函数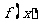 满足:
满足: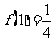 ,
,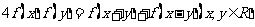 ,则
,则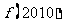 =_____________.
=_____________.
[答案]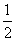
解析:取x=1 y=0得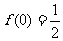
法一:通过计算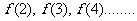 ,寻得周期为6
,寻得周期为6
法二:取x=n y=1,有f(n)=f(n+1)+f(n-1),同理f(n+1)=f(n+2)+f(n)
联立得f(n+2)=
-f(n-1) 所以T=6 故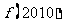 =f(0)=
=f(0)= 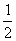 .
.
6.(天津卷文16)设函数f(x)=x-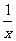 ,对任意x
,对任意x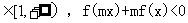 恒成立,则实数m的取值范围是________
恒成立,则实数m的取值范围是________
[答案]
[解析]因为对任意x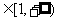 ,
,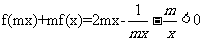 恒成立,所以
恒成立,所以
当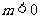 时,有
时,有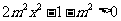 对任意x
对任意x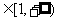 恒成立,即
恒成立,即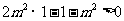 ,解得
,解得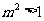 ,即
,即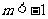 ;当
;当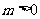 时,有
时,有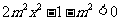 对任意x
对任意x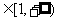 恒成立,x无解,综上所述实数m的取值范围是
恒成立,x无解,综上所述实数m的取值范围是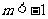 。
。
[命题意图]本题考查函数中的恒成立问题,考查函数与方程思想、转化与化归思想。
5.(天津卷理16)设函数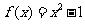 ,对任意
,对任意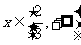 ,
,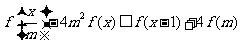 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .
[[答案]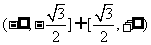
[解析]由题意知: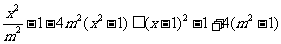 在
在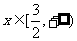 上恒成立,
上恒成立,
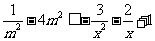 在
在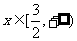 上恒成立,当
上恒成立,当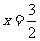 时,函数
时,函数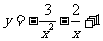 取得最小值
取得最小值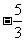 ,所以
,所以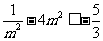 ,即
,即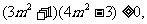 解得
解得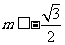 或
或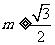 。
。
[命题意图]本题考查函数中的恒成立问题,考查化归与转化的数学思想。
4.(全国Ⅰ卷理15)直线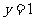 与曲线
与曲线 有四个交点,则
有四个交点,则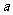 的取值范围是
的取值范围是
[答案](1,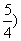
[命题意图]本小题主要考查函数的图像与性质、不等式的解法,着重考查了数形结合的数学思想.
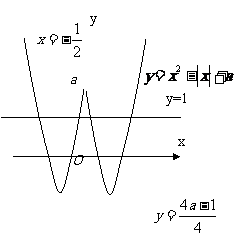 [解析]如图,在同一直角坐标系内画出直线
[解析]如图,在同一直角坐标系内画出直线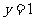 与曲线
与曲线
 ,观图可知,a的取值必须满足
,观图可知,a的取值必须满足
解得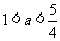 .
.
3.(江苏卷14)将边长为1的正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记S= ,则S的最小值是_______▲_______
,则S的最小值是_______▲_______
[答案]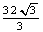
[解析] 考查函数中的建模应用,等价转化思想。一题多解。
设剪成的小正三角形的边长为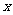 ,则:
,则: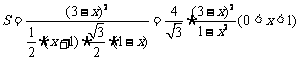
(方法一)利用函数的方法求最小值。
令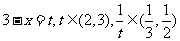 ,则:
,则: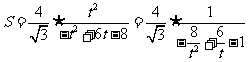
故当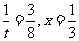 时,S的最小值是
时,S的最小值是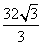 。
。
(方法二)利用导数求函数最小值。
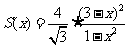 ,
,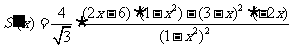

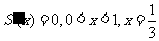 ,
,
当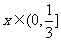 时,
时,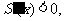 递减;当
递减;当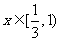 时,
时,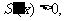 递增;
递增;
故当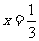 时,S的最小值是
时,S的最小值是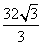 。
。
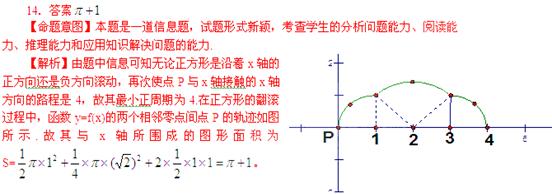
2. (北京卷文14)如图放置的边长为1的正方形PABC沿x轴滚动。设顶点p(x,y)的纵坐标与横坐标的函数关系是
(北京卷文14)如图放置的边长为1的正方形PABC沿x轴滚动。设顶点p(x,y)的纵坐标与横坐标的函数关系是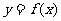 ,则
,则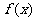 的最小正周期为
;
的最小正周期为
;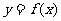 在其两个相邻零点间的图像与x轴所围区域的面积为
。说明:“正方形PABC沿x轴滚动”包含沿x轴正方向和沿x轴负方向滚动。沿x轴正方向滚动是指以顶点
在其两个相邻零点间的图像与x轴所围区域的面积为
。说明:“正方形PABC沿x轴滚动”包含沿x轴正方向和沿x轴负方向滚动。沿x轴正方向滚动是指以顶点 A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续,类似地,正方形PABC可以沿着x轴负方向滚动。
A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续,类似地,正方形PABC可以沿着x轴负方向滚动。
1. (北京卷理14)如图放置的边长为1的正方形PABC沿x轴滚动。设顶点p(x,y)的轨迹方程是
(北京卷理14)如图放置的边长为1的正方形PABC沿x轴滚动。设顶点p(x,y)的轨迹方程是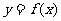 ,则
,则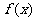 的最小正周期为
;
的最小正周期为
;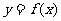 在其两个相邻零点间的图像与x轴所围区域的面积为
。
在其两个相邻零点间的图像与x轴所围区域的面积为
。
说明:“正方形PABC沿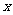 轴滚动”包括沿
轴滚动”包括沿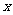 轴正方向和沿
轴正方向和沿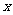 轴负方向滚动。沿
轴负方向滚动。沿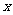 轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在
轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在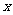 轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿
轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿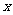 轴负方向滚动。
轴负方向滚动。
[答案]4,
解析:不难想象,从某一个顶点(比如A)落在x轴上的时候开始计算,到下一次A点落在x轴上,这个过程中四个顶点依次落在了x轴上,而每两个顶点间距离为正方形的边长1,因此该函数的周期为4。下面考察P点的运动轨迹,不妨考察正方形向右滚动,P点从x轴上开始运动的时候,首先是围绕A点运动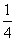 个圆,该圆半径为1,然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,然后以C为圆心,再旋转90°,这时候以CP为半径,因此最终构成图象如下:
个圆,该圆半径为1,然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,然后以C为圆心,再旋转90°,这时候以CP为半径,因此最终构成图象如下:
8.(浙江卷文9)已知x是函数f(x)=2 x+ 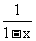 的一个零点,若
的一个零点,若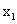 ∈(1,
∈(1,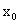 ),
),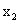 ∈(
∈(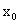 ,+
,+ ),则
),则
(A)f(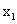 )<0,f(
)<0,f(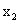 )<0
(B)f(
)<0
(B)f(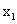 )<0,f(
)<0,f(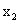 )>0
)>0
(C)f(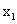 )>0,f(
)>0,f(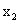 )<0
(D)f(
)<0
(D)f(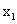 )>0,f(
)>0,f(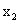 )>0
)>0
解析:选B,考察了数形结合的思想,以及函数零点的概念和零点的判断,属中档题
7.(天津卷文4)函数f(x)=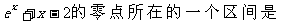
(A)(-2,-1) (B) (-1,0) (C) (0,1) (D) (1,2)
[答案]C
[解析]因为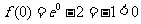 ,
,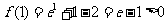 ,所以选C。
,所以选C。
[命题意图]本小题考查函数根的存在性定理,属基础题。
6.(天津卷理2)函数f(x)= 的零点所在的一个区间是
的零点所在的一个区间是
(A)(-2,-1) (B)(-1,0) (C)(0,1) (D)(1,2)
[答案]B
[解析]因为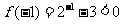 ,
,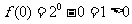 ,所以选B。
,所以选B。
[命题意图]本小题考查函数根的存在性定理,属基础题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com