
22.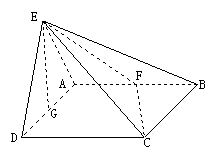 (本小题满分14分).如图所示,平面
(本小题满分14分).如图所示,平面 平面
平面 ,
, 是等边三角形,
是等边三角形,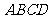 是矩形,
是矩形,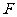 是
是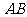 的中点,
的中点,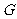 是
是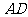 的中点,
的中点,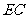 与平面
与平面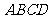 成
成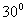 角
角
(1)求证: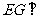 平面
平面 ;
;
(2)若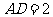 ,求二面角
,求二面角 的度数;
的度数;
(3)当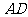 的长是多少时,
的长是多少时,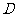 点到平面
点到平面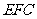 的距离为
的距离为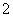 ?并说明理由
?并说明理由
四川省眉山中学2011级期末教学质量检测
21.(本题满分12分)已知{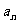 }(
}(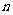 是正整数)是首项是
是正整数)是首项是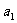 ,公比是
,公比是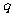 的等比数列
的等比数列
⑴求和: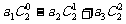 ;
;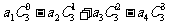 ;
;
⑵由(1)的结果归纳概括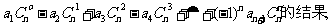
并加以证明.
20.(本题满分12分)甲、乙、丙三人组成一组,参加一个闯关游戏团体赛.三人各自独立闯关,其中甲闯关成功的概率为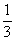 ,甲、乙都闯关成功的概率为
,甲、乙都闯关成功的概率为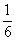 ,乙、丙都闯关成功的概率为
,乙、丙都闯关成功的概率为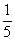 ,每人闯关成功得2分,三人得分之和记为小组团体总分.
,每人闯关成功得2分,三人得分之和记为小组团体总分.
(1)求乙、丙各自闯关成功的概率;
(2)求团体总分为4分的概率;
(3)若团体总分不小于4分,则小组可参加复赛,求该小组参加复赛的概率.
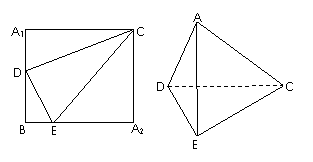
19.(本小题满分12分)如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1、A2重合于A,且二面角A-DC-E为直二面角。
(1)求证:CD⊥DE; (2)求AE与面DEC所成角的正弦.
18.(本小题满分12分)美国次贷危机引发全球金融动荡,波及中国沪深两大股市,甲、乙、丙3人打算趁股市低迷之际买入股票。三人商定在圈定的10只股票中各自随机购买1只(假定购买时,每只股票的基本情况完全相同)
(1)求甲、乙、丙3人恰好买到相同股票的概率;
(2)求甲、乙、丙3人中至少有2人买到相同股票的概率.
17.(本小题满分12分)
(1)已知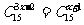 ,求
,求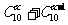 的值;
的值;
(2)若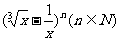 的展开式中第3项为常数项,求
的展开式中第3项为常数项,求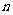 .
.
16.将边长为2,锐角为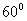 的菱形
的菱形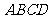 沿较短对角线
沿较短对角线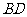 折成二面角
折成二面角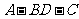 ,点
,点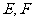 分别为
分别为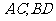 的中点,给出下列四个命题:
的中点,给出下列四个命题:
①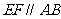 ;②
;②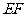 是异面直线
是异面直线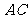 与
与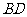 的公垂线;③当二面角
的公垂线;③当二面角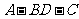 是直二面角时,
是直二面角时,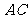 与
与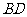 间的距离为
间的距离为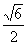 ;④
;④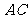 垂直于截面
垂直于截面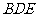 .
.
其中正确的是 (将正确命题的序号全填上).
15.将一个各个面上均涂有颜色的正方体锯成27个同样大小的小正方体,从这些小正方体中任取1个,其中恰有2面涂有颜色的概率是 .
14.已知二项式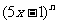 的展开式的所有项的系数的和为
的展开式的所有项的系数的和为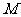 ,展开式的所有二项式的系数和为
,展开式的所有二项式的系数和为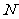 ,若
,若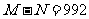 ,则
,则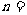 .
.
13.从A、B、C、D、E五名学生中选出四名分别参加数学、物理、化学、英语竞赛,其中A不参加物理、化学竞赛,则不同的参赛方案有 种.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com