
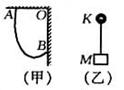
7.如图(甲)所示,将一条轻而柔软的细绳一端拴在天花板上的A点.另一端拴在竖直墙上的B点,A和B到O点的距离相等,绳的长度是OA的两倍。图(乙)所示为一质量可忽略的动滑轮K,滑轮下悬挂一质量为m的重物,设摩擦力可忽略,现将动滑轮和重物一起挂到细绳上,在达到平衡时,绳所受的拉力是多大?

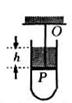
6.如图所示,玻璃管内活塞P下方封闭着空气,P上有细线系住,线上端悬于O点,P的上方有高h的水银柱,如不计水银、活塞P与玻璃管的摩擦,大气压强为p0保持不变,则当气体温度升高时(水银不溢出)( )
A.管内空气压强恒为(p0十ρgh)(ρ为水银密度)
B.管内空气压强将升高
C.细线上的拉力将减小
D.玻璃管位置降低
5.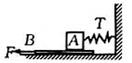 如图所示,一个本块A放在长木板B上,长木板B放在水平地面上.在恒力F作用下,长木板B以速度v匀速运动,水平弹簧秤的示数为T.下列关于摩擦力正确的是( )
如图所示,一个本块A放在长木板B上,长木板B放在水平地面上.在恒力F作用下,长木板B以速度v匀速运动,水平弹簧秤的示数为T.下列关于摩擦力正确的是( )
A.木块A受到的滑动摩擦力的大小等于T
B.木块A受到的静摩擦力的大小等于T
C.若长木板B以2v的速度匀速运动时,木块A受到的摩擦力大小等于2T
D.若用2F的力作用在长木板上,木块A受到的摩擦力的大小等于T
4.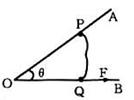 如图所示,两光滑硬杆AOB成θ角,在两杆上各套上轻环P、Q,两环用细绳相连,现用恒力F沿OB方向拉环Q ,当两环稳定时细绳拉力为( )
如图所示,两光滑硬杆AOB成θ角,在两杆上各套上轻环P、Q,两环用细绳相连,现用恒力F沿OB方向拉环Q ,当两环稳定时细绳拉力为( )
A.Fsinθ B.F/sinθ
C.Fcosθ D.F/cosθ
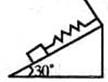
1.把重20N的物体放在倾角为30°的粗糙斜面上,物体右端与固定在斜面上的轻弹簧相连接,如图所示,若物体与斜面间的最大静摩擦力为 12 N,则弹簧的弹力为( )
A.可以是22N,方向沿斜面向上
B.可以是2N.方向沿斜面向上
 C.可以是2N,方向沿斜面向下
C.可以是2N,方向沿斜面向下
D.可能为零
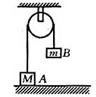
2两个物体A和B,质量分别为M和m,用跨过定滑轮的轻绳相连, A静止于水平地面上,如图所示,不计摩擦力,A对绳的作用力的大小与地面对A的作用力的大小分别为()
A.mg,(M-m)g B.mg,Mg
C.(M-m)g, M g D.(M+m)g,(M-m)g
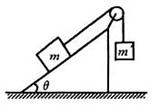 3如图所示,当倾角为45°时物体m处于静止状态,当倾角θ再增大一些,物体m仍然静止(绳子质量、滑轮摩擦不计)下列说法正确的是( )
3如图所示,当倾角为45°时物体m处于静止状态,当倾角θ再增大一些,物体m仍然静止(绳子质量、滑轮摩擦不计)下列说法正确的是( )
A.绳子受的拉力增大
B.物林m对斜面的正压力减小
C.物体m受到的静摩擦力可能增大
D.物体m受到的静摩擦力可能减小
3、动态平衡问题:解析法和图象法。
解析法:对研究对象形的任一状态进行受力分析,建立平衡方程,求出因变量与自变量的一般函数关系,然后根据自变量变化情况而确定因变量的变化情况。
图象法:对研究对象在状态变化过程中的若干状态进行受力分析,依据某一参量的变化,在同一图中作出若干状态下的平衡图,再由边角变化关系确定某些力的大小及方向的变化情况。
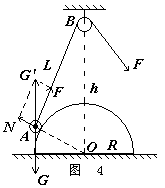
[例14]如图所示,在半径为R的光滑半球面正上方距球心h处悬挂一定滑轮,重为G的小球A用绕过滑轮的绳子被站在地面上的人拉住。人拉动绳子,在与球面相切的某点缓慢运动到接近顶点的过程中,试分析半球对小球的支持力N和绳子拉力F如何变化。
解析:小球在重力G,球面的支持力N,绳子的拉力F作用下,处于动态平衡。任选一状态,受力如图4所示。不难看出,力三角形ΔFAG’与几何关系三角形ΔBAO相似,从而有:
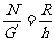 ,
, 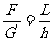
(其中G’与G等大,L为绳子AB的长度)
 由于在拉动过程中,R、h不变,绳长L在减小,可见:球面的支持力
由于在拉动过程中,R、h不变,绳长L在减小,可见:球面的支持力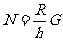 大小不变,绳子的拉力
大小不变,绳子的拉力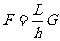 在减小。
在减小。
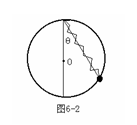
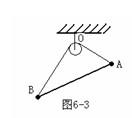
例15图6-2所示,小圆环重G,固定的竖直大环半径为R,轻弹簧原长为L(L﹤R)其倔强系数为K,接触面光滑,求小环静止时弹簧与竖直方向的夹角θ?
 提示:可利用正弦定律求解或三角形相似法求解
提示:可利用正弦定律求解或三角形相似法求解
例34、如图6-3所示,一轻杆两端固结两个小物体A、B,mA=4mB
跨过滑轮连接A和B的轻绳长为L,求平衡时OA和OB分别多长?
 针对训练
针对训练
2、多力合成时为了便于计算,往往把这些力先正交分解,根据:∑FX=0 ∑FY=0 求解。
1、物体受三力作用而平衡,且三力成一定的夹角,一般将三力平衡化为二力平衡,对应数学方法:
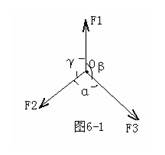
(1)正弦定理:如图6-1所示,则有F1/sinα=F2/sinβ=F3/sinγ
(2)三角形相似:这种方法应用广泛,具体应用时先画出力的
三角形,再寻找与力的三角形相似的空间三角形,(即具有物理
意义的三角形和具有几何意义的三角形相似)由相似三角形建立
比例关系求解。
6.绳中张力问题的求解
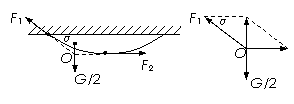 [例13]重G的均匀绳两端悬于水平天花板上的A、B两点。静止时绳两端的切线方向与天花板成α角。求绳的A端所受拉力F1和绳中点C处的张力F2。
[例13]重G的均匀绳两端悬于水平天花板上的A、B两点。静止时绳两端的切线方向与天花板成α角。求绳的A端所受拉力F1和绳中点C处的张力F2。
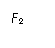 解:以AC段绳为研究对象,根据判定定理,虽然AC所受的三个力分别作用在不同的点(如图中的A、C、P点),但它们必为共点力。设它们延长线的交点为O,用平行四边形定则作图可得:
解:以AC段绳为研究对象,根据判定定理,虽然AC所受的三个力分别作用在不同的点(如图中的A、C、P点),但它们必为共点力。设它们延长线的交点为O,用平行四边形定则作图可得: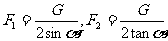
 7 解答平衡问题时常用的数学方法
7 解答平衡问题时常用的数学方法
根据平衡条件解答平衡问题,往往要进行一定的数学运算才能求得结果,在选择数学方法可针对如下几种情况进行:
5.“稳态速度”类问题中的平衡
[例12物体从高空下落时,空气阻力随速度的增大而增大,因此经过一段距离后将匀速下落,这个速度称为此物体下落的稳态速度。已知球形物体速度不大时所受的空气阻力正比于速度v,且正比于球半径r,即阻力f=krv,k是比例系数。对于常温下的空气,比例系数k=3.4×10-4Ns/m2。已知水的密度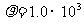 kg/m3,重力加速度为
kg/m3,重力加速度为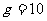 m/s2。求半径r=0.10mm的球形雨滴在无风情况下的稳态速度。
m/s2。求半径r=0.10mm的球形雨滴在无风情况下的稳态速度。
解析:雨滴下落时受两个力作用:重力,方向向下;空气阻力,方向向上。当雨滴达到稳态速度后,加速度为0,二力平衡,用m表示雨滴质量,有mg-krv=0,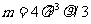 ,求得
,求得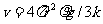 ,v=1.2m/s。
,v=1.2m/s。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com