5．在平面解析几何初步的教学中，教师应帮助学生经历如下的过程：首先

将几何问题代数化，用代数的语言描述几何要素及其关系，进而将几何问题转化为代数问题；处理代数问题；分析代数结果的几何含义，最终解决几何问题。这种思想应贯穿平面解析几何教学的始终，帮助学生不断地体会“数形结合”的思想方法。

参考案例

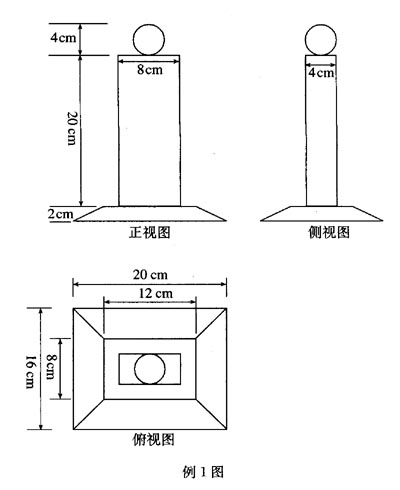
例1 如图这是一个奖杯的三视图，请你画出它的直观图，并求出这个奖杯的体积。

例2 观察自己的教室，说出观察到的点、线、面之间的位置关系，并说明理由。

数学3

在本模块中，学生将学习算法初步、统计、概率。

　算法是数学及其应用的重要组成部分，是计算科学的重要基础。随着现代信息技术飞速发展，算法在科学技术、社会发展中发挥着越来越大的作用，并日益融入社会生活的许多方面，算法思想已经成为现代人应具备的一种数学素养。需要特别指出的是，中国古代数学中蕴涵了丰富的算法思想。在本模块中，学生将在义务教育阶段初步感受算法思想的基础上，结合对具体数学实例的分析，体验程序框图在解决问题中的作用；通过模仿、操作、探索，学习设计程序框图表达解决问题的过程；体会算法的基本思想以及算法的重要性和有效性，发展有条理的思考与表达的能力，提高逻辑思维能力。

　现代社会是信息化的社会，人们常常需要收集数据，根据所获得的数据提取有价值的信息，作出合理的决策。统计是研究如何合理收集、整理、分析数据的学科，它可以为人们制定决策提供依据。随机现象在日常生活中随处可见，概率是研究随机现象规律的学科，它为人们认识客观世界提供了重要的思维模式和解决问题的方法，同时为统计学的发展提供了理论基础。因此，统计与概率的基础知识已经成为一个未来公民的必备常识。在本模块中，学生将在义务教育阶段学习统计与概率的基础上，通过实际问题情境，学习随机抽样、样本估计总体、线性回归的基本方法，体会用样本估计总体及其特征的思想；通过解决实际问题，较为系统地经历数据收集与处理的全过程，体会统计思维与确定性思维的差异。学生将结合具体实例，学习概率的某些基本性质和简单的概率模型，加深对随机现象的理解，能通过实验、计算器(机)模拟估计简单随机事件发生的概率。

　内容与要求

4．有条件的学校应在教学过程中恰当地使用现代信息技术展示空间图形，为理解和掌握图形几何性质(包括证明)的教学提供形象的支持，提高学生的几何直观能力。教师可以指导和帮助学生运用立体几何知识选择课题，进行探究。

3．立体几何初步的教学中，要求对有关线面平行、垂直关系的性质定理进行证明；对相应的判定定理只要求直观感知、操作确认，在选修系列2中将用向量方法加以论证。

2．几何教学应注意引导学生通过对实际模型的认识，学会将自然语言转化为图形语言和符号语言。教师可以使用具体的长方体的点、线、面关系作为载体，使学生在直观感知的基础上，认识空间中一般的点、线、面之间的位置关系；通过对图形的观察、实验和说理，使学生进一步了解平行、垂直关系的基本性质以及判定方法，学会准确地使用数学语言表述几何对象的位置关系，并能解决一些简单的推理论证及应用问题(参见例2)。

1．立体几何初步的教学重点是帮助学生逐步形成空间想像能力。本部分内容的设计遵循从整体到局部、具体到抽象的原则，教师应提供丰富的实物模型或利用计算机软件呈现的空间几何体，帮助学生认识空间几何体的结构特征，并能运用这些特征描述现实生活中简单物体的结构，巩固和提高义务教育阶段有关三视图的学习和理解，帮助学生运用平行投影与中心投影，进一步掌握在平面上表示空间图形的方法和技能(参见例1)。

2．平面解析几何初步(约18课时)

(1)直线与方程

①在平面直角坐标系中，结合具体图形，探索确定直线位置的几何要素。

②理解直线的倾斜角和斜率的概念，经历用代数方法刻画直线斜率的过程，掌握过两点的直线斜率的计算公式。

③能根据斜率判定两条直线平行或垂直。

④根据确定直线位置的几何要素，探索并掌握直线方程的几种形式(点斜式、两点式及一般式)，体会斜截式与一次函数的关系。

⑤能用解方程组的方法求两直线的交点坐标。

⑥探索并掌握两点间的距离公式、点到直线的距离公式，会求两条平行直线间的距离。

(2)圆与方程

①回顾确定圆的几何要素，在平面直角坐标系中，探索并掌握圆的标准方程与一般方程。

②能根据给定直线、圆的方程，判断直线与圆、圆与圆的位置关系。

③能用直线和圆的方程解决一些简单的问题。

(3)在平面解析几何初步的学习过程中，体会用代数方法处理几何问题的思想。

(4)空间直角坐标系

①通过具体情境，感受建立空间直角坐标系的必要性，了解空间直角坐标系，会用空间直角坐标系刻画点的位置。

②通过表示特殊长方体(所有棱分别与坐标轴平行)顶点的坐标，探索并得出空间两点间的距离公式。

说明与建议

1．立体几何初步(约18课时)

(1)空间几何体

① 利用实物模型、计算机软件观察大量空间图形，认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构。

② 能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图，能识别上述的三视图所表示的立体模型，会使用材料(如纸板)制作模型，会用斜二侧法画出它们的直观图。

③ 通过观察用两种方法(平行投影与中心投影)画出的视图与直观图，了解空间图形的不同表示形式。

④ 完成实习作业，如画出某些建筑的视图与直观图(在不影响图形特征的基础上，尺寸、线条等不作严格要求)。

⑤ 了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式)。

(2)点、线、面之间的位置关系

① 借助长方体模型，在直观认识和理解空间点、线、面的位置关系的基础上，抽象出空间线、面位置关系的定义，并了解如下可以作为推理依据的公理和定理。

◆公理1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内。

◆公理2：过不在一条直线上的三点，有且只有一个平面。

◆公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

◆公理4：平行于同一条直线的两条直线平行。

◆定理：空间中如果两个角的两条边分别对应平行，那么这两个角相等或互补。

②以立体几何的上述定义、公理和定理为出发点，通过直观感知、操作确认、思辨论证，认识和理解空间中线面平行、垂直的有关性质与判定。

通过直观感知、操作确认，归纳出以下判定定理。

◆平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

◆一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

◆一条直线与一个平面内的两条相交直线垂直，则该直线与此平面垂直。

◆ 一个平面过另一个平面的垂线，则两个平面垂直。

通过直观感知、操作确认，归纳出以下性质定理，并加以证明。

◆一条直线与一个平面平行，则过该直线的任一个平面与此平面的交线与该直线平行。

◆两个平面平行，则任意一个平面与这两个平面相交所得的交线相互平行。

◆垂直于同一个平面的两条直线平行。

◆两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。

③能运用已获得的结论证明一些空间位置关系的简单命题。

7．应注意鼓励学生运用现代教育技术学习、探索和解决问题。例如，利用计算器、计算机画出指数函数、对数函数等的图象，探索、比较它们的变化规律，研究函数的性质，求方程的近似解等。

参考案例

例1 田径队的小刚同学，在教练指导下进行3 000米跑的训练，训练计划要求是：

(1)起跑后，匀加速，10秒后达到每秒5米的速度，然后匀速跑到2分；

(2)开始均匀减速，到5分时已减到每秒4米，再保持匀速跑4分时间；

(3)在1分之内，逐渐加速达到每秒5米的速度，保持匀速往下跑；

(4)最后200米，均匀加速冲刺，使撞线时的速度达到每秒8米。

请按照上面的要求，解决下面的问题。

(1)画出小刚跑步的时间与速度的函数图象。

(2)写出小刚进行长跑训练时，跑步速度关于时间的函数。

(3)按照上边的要求，计算跑完3 000米的所用时间。

解：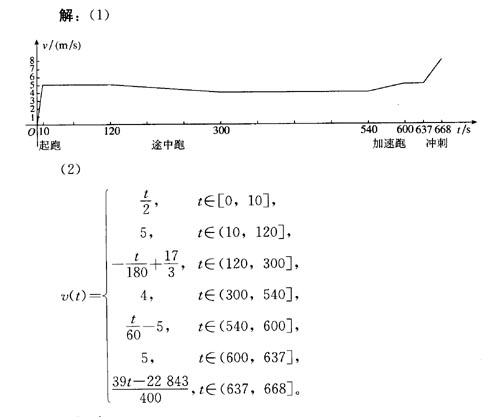

例2 家用电器(如冰箱等)使用的氟化物的释放破坏了大气上层的臭氧层。臭氧含量Q呈指数函数型变化，满足关系式Q =Q₀e^-0.0025t，其Q₀是臭氧的初始量。

(1)随时间的增加，臭氧的含量是增加还是减少？

(2)多少年以后将会有一半的臭氧消失？

数学2

在本模块中，学生将学习立体几何初步、平面解析几何初步。

几何学是研究现实世界中物体的形状、大小与位置关系的数学学科。人们通常采用直观感知、操作确认、思辨论证、度量计算等方法认识和探索几何图形及其性质。三维空间是人类生存的现实空间，认识空间图形，培养和发展学生的空间想像能力、推理论证能力、运用图形语言进行交流的能力以及几何直观能力，是高中阶段数学必修系列课程的基本要求。在立体几何初步部分，学生将先从对空间几何体的整体观察入手，认识空间图形；再以长方体为载体，直观认识和理解空间点、线、面的位置关系；能用数学语言表述有关平行、垂直的性质与判定，并对某些结论进行论证。学生还将了解一些简单几何体的表面积.

解析几何是17世纪数学发展的重大成果之一，其本质是用代数方法研究图形的几何性质，体现了数形结合的重要数学思想。在本模块中，学生将在平面直角坐标系中建立直线和圆的代数方程，运用代数方法研究它们的几何性质及其相互位置关系，并了解空间直角坐标系。体会数形结合的思想，初步形成用代数方法解决几何问题的能力。

内容与要求

6．在函数应用的教学中，教师要引导学生不断地体验函数是描述客观世界变化规律的基本数学模型，体验指数函数、对数函数等函数与现实世界的密切联系及其在刻画现实问题中的作用。

5．反函数的处理，只要求以具体函数为例进行解释和直观理解，例如，可通过比较同底的指数函数和对数函数，说明指数函数y=ax和对数函数y=loga x互为反函数(a > 0,a≠1)。不要求一般地讨论形式化的反函数定义，也不要求求已知函数的反函数。