6．在教学中，要防止将导数仅仅作为一些规则和步骤来学习，而忽视它的思想和价值。应使学生认识到，任何事物的变化率都可以用导数来描述。应当避免过量的形式化运算练习。

　参考案例

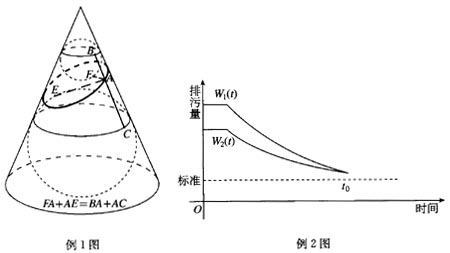
　例1 如图，用一个平面去截圆锥，这个平面与圆锥的交线是一个椭圆。在圆锥内做大小两个球分别与圆锥和截面相切。那么，截面与两个球的切点恰是椭圆的两个焦点。

　例2 国家环保局在规定的排污达标的日期前，对甲、乙两家企业进行检查，其连续检测结果如图所示。试问哪个企业治污效果好(其中W表示治污量)。

　在t₀处，虽然W₁(t₀)=W₂(t₀)，然而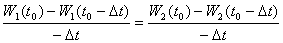，所以说在单位时间里企业甲比企业乙的平均治污率大，因此企业甲比企业乙略好一筹。

　例3 我们知道，当运动员从10米高台跳水时，从腾空到进入水面的过程中，不同时刻的速度是不同的。假设t秒后运动员相对地面的高度为：，在2秒时运动员的速度(瞬时速度)为多少？

　该运动员在2秒内到2．1秒(记为［2，2．1］)平均速度为

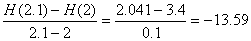
　同样，可以计算出［2，2．1］［2，2．001］，…的平均速度，也可以计算出［1．99，2］，［1．999，2］…的平均速度。

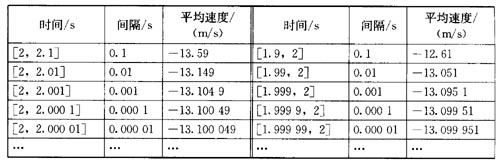
　由此可以看出,当时间间隔越来越小时，平均速度趋于一个常数，这一常数(13.1)就可作为该运动员在2秒时的速度。

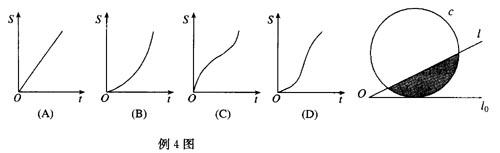
　例4 如图，直线l和圆c，当l从l0开始在平面上绕点O匀速旋转(旋转角度不超过90o)时，它扫过的圆内阴影部分的面积S是时间t的函数，它的图象大致是( )。

　例5 有一边长为a的正方形铁片，铁片的四角截去四个边长为x的小正方形，然后做成一个无盖方盒。

　(1)试把方盒的容积V表示x的函数。

　(2)求x多大时，做成方盒的容积V最大。

　选修1-2

　在本模块中，学生将学习统计案例、推理与证明、数系扩充及复数的引入、框图。

　学生将在必修课程学习统计的基础上，通过对典型案例的讨论，了解和使用一些常用的统计方法，进一步体会运用统计方法解决实际问题的基本思想，认识统计方法在决策中的作用。

　“推理与证明”是数学的基本思维过程，也是人们学习和生活中经常使用的思维方式。推理一般包括合情推理和演绎推理。合情推理是根据已有的事实和正确的结论(包括定义、公理、定理等)、实验和实践的结果，以及个人的经验和直觉等推测某些结果的推理过程。归纳、类比是合情推理常用的思维方法。在解决问题的过程中，合情推理具有猜测和发现结论、探索和提供思路的作用，有利于创新意识的培养。演绎推理是根据已有的事实和正确的结论(包括定义、公理、定理等)，按照严格的逻辑法则得到新结论的推理过程，培养和提高学生的演绎推理或逻辑证明的能力是高中数学课程的重要目标。合情推理和演绎推理之间联系紧密、相辅相成。证明通常包括逻辑证明和实验、实践证明，数学结论的正确性必须通过演绎推理或逻辑证明来保证，即在前提正确的基础上，通过正确使用推理规则得出结论。在本模块中，学生将通过对已学知识的回顾，进一步体会合情推理、演绎推理以及二者之间的联系与差异；体会数学证明的特点，了解数学证明的基本方法,包括直接证明的方法(如分析法、综合法)和间接证明的方法(如反证法)；感受逻辑证明在数学以及日常生活中的作用，养成言之有理、论证有据的习惯。

　数系扩充的过程体现了数学的发现和创造过程，同时体现了数学发生、发展的客观需求，复数的引入是中学阶段数系的又一次扩充。在本模块中，学生将在问题情境中了解数系扩充的过程以及引入复数的必要性，学习复数的一些基本知识，体会人类理性思维在数系扩充中的作用。

　框图是表示一个系统各部分和各环节之间关系的图示，它的作用在于能够清晰地表达比较复杂的系统各部分之间的关系。框图已经广泛应用于算法、计算机程序设计、工序流程的表述、设计方案的比较等方面，也是表示数学计算与证明过程中主要逻辑步骤的工具，并将成为日常生活和各门学科中进行交流的一种常用表达方式。在本模块中，学生将学习用“流程图”“结构图”等刻画数学问题以及其他问题的解决过程；并在学习过程中，体验用框图表示数学问题解决过程以及事物发生、发展过程的优越性，提高抽象概括能力和逻辑思维能力，能清晰地表达和交流思想。

　内容与要求

5．本模块中，导数的概念是通过实际背景和具体应用的实例引入的。教学中，可以通过研究增长率、膨胀率、效率、密度、速度等反映导数应用的实例，引导学生经历由平均变化率到瞬时变化率的过程，知道瞬时变化率就是导数。通过感受导数在研究函数和解决实际问题中的作用，体会导数的思想及其内涵。这样处理的目的是帮助学生直观理解导数的背景、思想和作用。

4．教师应向学生展现圆锥曲线在实际中的应用，例如，投掷铅球的运行轨迹，卫星的运行轨迹等。

3．教师应向学生展示平面截圆锥得到椭圆的过程，使学生加深对圆锥曲线的理解。有条件的学校应充分发挥现代教育技术的作用，利用计算机演示平面截圆锥所得的圆锥曲线(参见例1)。

2．在引入圆锥曲线时，应通过丰富的实例(如行星运行轨道、抛物运动轨迹、探照灯的镜面)，使学生了解圆锥曲线的背景与应用。

1．在常用逻辑用语教学中，应特别注意以下几个问题。

　(1)这里考虑的命题是指明确地给出条件和结论的命题，对“命题的逆命题、否命题与逆否命题”只要求作一般性了解，重点关注四种命题的相互关系和命题的必要条件、充分条件、充要条件。

　(2)对逻辑联结词“或”“且”“非”的含义，只要求通过数学实例加以了解，使学生正确地表述相关的数学内容。

　(3)对于量词，重在理解它们的含义，不要追求它们的形式化定义。

　(4)注意引导学生在使用常用逻辑用语的过程中，掌握常用逻辑用语的用法，纠正出现的逻辑错误，体会运用常用逻辑用语表述数学内容的准确性、简洁性。避免对逻辑用语的机械记忆和抽象解释，不要求使用真值表。

3．导数及其应用(约16课时)

　(1)导数概念及其几何意义

　①通过对大量实例的分析，经历由平均变化率过渡到瞬时变化率的过程，了解导数概念的实际背景，知道瞬时变化率就是导数，体会导数的思想及其内涵(参见例2、例3)。

　②通过函数图象直观地理解导数的几何意义。

　(2)导数的运算

　① 能根据导数定义，求函数y=c，y=x，y=x²，y=1/x的导数。

　② 能利用给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数。

　③ 会使用导数公式表。

　(3)导数在研究函数中的应用

　① 结合实例，借助几何直观探索并了解函数的单调性与导数的关系(参见例4)；能利用导数研究函数的单调性，会求不超过三次的多项式函数的单调区间。

　② 结合函数的图象，了解函数在某点取得极值的必要条件和充分条件；会用导数求不超过三次的多项式函数的极大值、极小值，以及在给定区间上不超过三次的多项式函数的最大值、最小值。

　(4)生活中的优化问题举例

　例如，通过使利润最大、用料最省、效率最高等优化问题，体会导数在解决实际问题中的作用(参见例5)。

　(5)数学文化

　收集有关微积分创立的时代背景和有关人物的资料，并进行交流；体会微积分的建立在人类文化发展中的意义和价值。具体要求见本标准中“数学文化”的要求。

　说明与建议

2．圆锥曲线与方程(约12课时)

　(1)了解圆锥曲线的实际背景，感受圆锥曲线在刻画现实世界和解决实际问题中的作用。

　(2)经历从具体情境中抽象出椭圆模型的过程(参见例1)，掌握椭圆的定义、标准方程及简单几何性质。

　(3)了解抛物线、双曲线的定义、几何图形和标准方程，知道它们的简单几何性质。

　(4)通过圆锥曲线与方程的学习，进一步体会数形结合的思想。

　(5)了解圆锥曲线的简单应用。

6．线性规划是优化的具体模型之一。在本模块的教学中，教师应引导学生体会线性规划的基本思想，借助几何直观解决一些简单的线性规划问题，不必引入很多名词。

　参考案例

　例1 教育储蓄的收益与比较

　要求学生收集本地区有关教育储蓄的信息，思考以下问题。

　(1)依教育储蓄的方式，每月存50元，连续存3年，到期(3年)或6年时一次可支取本息共多少元？

　(2)依教育储蓄的方式，每月存a元，连续存3年，到期(3年)或6年时一次可支取本息共多少元？

　(3)依教育储蓄的方式，每月存50元，连续存3年，到期(3年)时一次可支取本息比同档次的“零存整取”多收益多少元？

　(4)欲在3年后一次支取教育储蓄本息合计1万元，每月应存入多少元？

　(5)欲在3年后一次支取教育储蓄本息合计a万元，每月应存入多少元？

　(6)依教育储蓄的方式，原打算每月存100元，连续存6年，可是到4年时，学生需要提前支取全部本息，一次可支取本息共多少元？

　(7)依教育储蓄的方式，原打算每月存a元，连续存6年，可是到b年时，学生需要提前支取全部本息，一次可支取本息共多少元？

　(8)开放题：不用教育储蓄的方式, 而用其他的储蓄形式, 以每月可存100元, 6年后使用为例, 探讨以现行的利率标准可能的最大收益, 将得到的结果与教育储蓄比较。

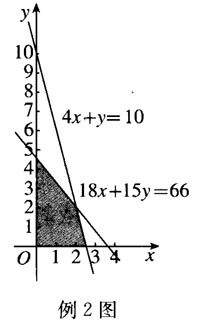
　例2 一个化肥厂生产甲、乙两种混合肥料，生产1车皮甲种肥料需要的主要原料是磷酸盐4吨、硝酸盐18吨，产生的利润为10 000元；生产1车皮乙种肥料需要的主要原料是磷酸盐1吨、硝酸盐15吨，产生的利润为5 000元。现有库存磷酸盐10吨、硝酸盐66吨，在此基础上进行生产。请列出条件的数学关系式，并画出其图象。

　解：设x，y分别为计划生甲、乙两种混合肥料的车皮数，于是　

　解：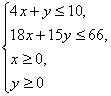

　例3 某厂拟生产甲、乙两种适销产品，每件销售收入分别为3千元、2千元。甲、乙产品都需要在A，B两种设备上加工，在每台A，B上加工一件甲所需工时分别为1时、2时，加工一件乙所需工时分别为2时、1时，A，B两种设备每月有效使用台时数分别为400和500。如何安排生产可使收入最大？

　解：这个问题的数学模型是二元线性规划。

　设甲、乙两种产品的产量分别为x，y件，约束条件是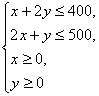，目标函数是f＝3x+2y。

　要求出适当的x，y，使f＝3x+2y取得最大值。

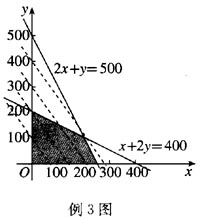
　先要画出可行域，如图。考虑3x+2y=2a，a是参数，将它变形为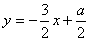，这是斜率为－3/2，随a变化的一族直线。a/2是直线在y轴上截距，当a/2最大时a最大，当然直线要与可行域相交，即在满足约束条件时目标函数取得最大值。

　在这个问题中，使3x+2y取得最大值的(x，y)是两直线2x+y＝500与x+2y＝400的交点(200，100)。

　因此，甲、乙两种产品的每月产时不时分别为200、100件时，可得最大收入800千元。

　例4 某工厂建造一个长方体无盖贮水池，其容积为4800 m3，深度为3 m。如果池底每1 m2的造价为150元，池壁每1 m2的造价为120元，怎样设计水池能使总造价最低，最低总造价是多少元？