
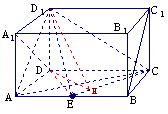
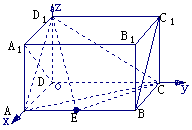
18.如图,在长方体AC1中,AD=AA1=1,AB=2,点E在棱AB上移动.
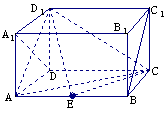 (1)证明:D1E⊥A1D;
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为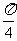 .
.
解:法1(1)∵AE⊥面AA1DD1,A1D⊥AD1,∴A1D⊥D1E
(2)设点E到面ACD1的距离为h,在△ACD1中,AC=CD1=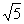 ,AD1=
,AD1=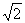 ,
,
故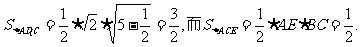
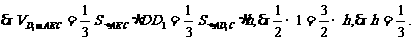
(3)过D作DH⊥CE于H,连D1H、DE,则D1H⊥CE,
 ∴∠DHD1为二面角D1-EC-D的平面角.
∴∠DHD1为二面角D1-EC-D的平面角.
设AE=x,则BE=2-x
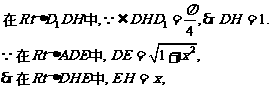

法2:以D为坐标原点,直线DA、DC、DD1分别为x、y、z轴,建立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A(1,0,0), C(0,2,0).
 (1)
(1)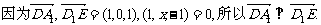
(2)因为E为AB的中点,则E(1,1,0),
从而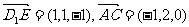 ,
,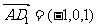 ,
,
设平面ACD1的法向量为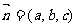 ,
,
则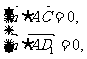 也即
也即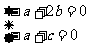 ,得
,得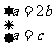 ,
,
从而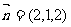 ,所以点E到平面AD1C的距离为
,所以点E到平面AD1C的距离为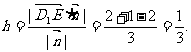
(3)设平面D1EC的法向量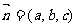 ∴
∴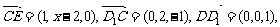
由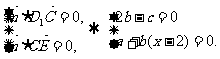 令b=1, ∴c=2, a=2-x,
令b=1, ∴c=2, a=2-x,
∴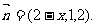 依题意
依题意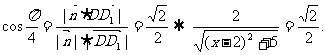
∴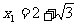 (不合,舍去),
(不合,舍去),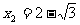 .
.
∴AE=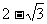 时,二面角D1-EC-D的大小为
时,二面角D1-EC-D的大小为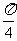 .
.
17。解:(Ⅰ)当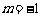 时,
时,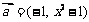 ,
,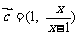 .
.
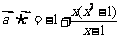
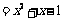 . ………………………………………
2分
. ………………………………………
2分
∵
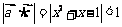 ,
,
∴ 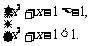 解得
解得
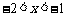 或
或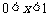 .
.
∴ 当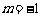 时,使不等式
时,使不等式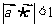 成立的x的取值范围是
成立的x的取值范围是
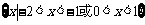 .…………………………………………… 5分
.…………………………………………… 5分
(Ⅱ)∵ 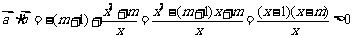 ,…… 8分
,…… 8分
∴ 当m<0时,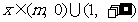 ;
;
当m=0时, 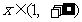 ;
;
当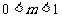 时,
时,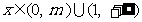 ;
;
当m=1时,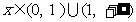 ;
;
当m>1时,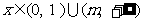 ----------------------------------12分
----------------------------------12分
17.(本小题12分)已知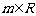 ,
, 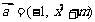 ,
,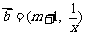 ,
,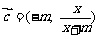 .
.
(1)当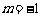 时,求使不等式
时,求使不等式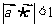 成立的x的取值范围;
成立的x的取值范围;
(2)求使不等式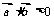 成立的x的取值范围.
成立的x的取值范围.
16.(本小题12分)已知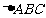 中,
中,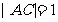 ,
,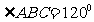 ,
,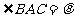 ,
,
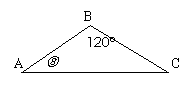 记
记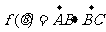 ,(1)求
,(1)求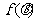 关于
关于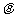 的表达式;(2)求
的表达式;(2)求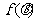 的值域;
的值域;
16解:(1)由正弦定理有: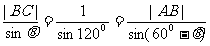 ;。。。。。(2分)
;。。。。。(2分)
∴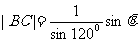 ,
,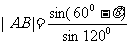 ;。。。。。。。。。。。。。(4分)
;。。。。。。。。。。。。。(4分)
∴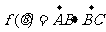
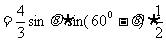
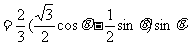
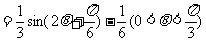 。。。。。。。。。。。。。。。。。。。(7分)
。。。。。。。。。。。。。。。。。。。(7分)
(2)由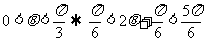 ;。。。。。。。。。。。。。。。。。。。。。。(8分)
;。。。。。。。。。。。。。。。。。。。。。。(8分)
∴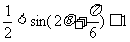 ;。。。。。。。。(10分)∴
;。。。。。。。。(10分)∴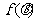
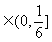 。。。。。。。。。。。。。(12分)
。。。。。。。。。。。。。(12分)
14.[解析] 解答本题要灵活应用等差数列性质.由已知条件
即a6>0,a7<0,a6+a7>0,因此d<0,①正确;
S11=11a6>0②正确;S12==>0,故③错误;
S13==12a7<0,故④错误,
故真命题的序号是①②.[答案] ①②
14
15已知实数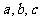
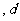 满足
满足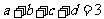 ,
,
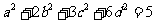 试求
试求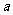 的最值
的最值
解:由柯西不等式得,有

即,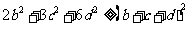 由条件可得,
由条件可得,
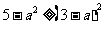
解得,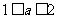 当且仅当
当且仅当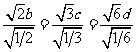 时等号成立,
时等号成立,
代入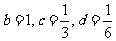 时,
时, 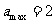
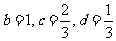 时
时
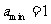
13.已知Sn是公差为d的等差数列{an}的前n项和,且S6>S7>S5,则下列四个命题:①d<0;②S11>0;③S12<0;④S13>0中真命题的序号为________.
12.[解析] 依题意有g(x)
=x2f(x-1)=,
所以g(x)的递减区间是(0,1).[答案] (0,1)
12.设函数f(x)=,g(x)=x2f(x-1),
则函数g(x)的递减区间是________.
11、解析:若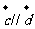 ,则
,则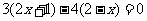 ,解得
,解得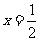 .
.
8. A.(6,+∞) B . [6,+∞)
C
.(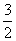 ,+∞)
D . [
,+∞)
D . [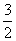 ,+∞)
,+∞)
D 当ω>0时,
-ω≤ωx≤ω,由题意知-ω≤-,即ω≥,
9 B.
10给出定义:若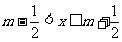 (其中m为整数),则m 叫做离实数x最近的整数,记作
(其中m为整数),则m 叫做离实数x最近的整数,记作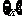 = m. 在此基础上给出下列关于函数
= m. 在此基础上给出下列关于函数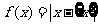 的四个命题:
的四个命题:
①函数y=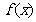 的定义域为R,值域为
的定义域为R,值域为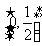 ;
;
②函数y=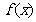 的图像关于直线
的图像关于直线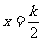 (
(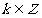 )对称;
)对称;
③函数y=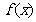 是周期函数,最小正周期为1;
是周期函数,最小正周期为1;
④函数y=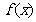 在
在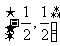 上是增函数。
上是增函数。
其中正确的命题的序号是( )
A. ① B. ②③ C ①②③ D ①④
10 C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com