
1.根据物质的溶解性“相似相溶”的一般规律,说明溴、碘单质在四氯化碳中比在水中溶解度大,说明正确的是( )
A.溴、碘单质和四氯化碳中都含有卤素
B.溴、碘是单质,四氯化碳是化合物
C.Cl2、Br2、I2是非极性分子,CCl4也是非极性分子,而水是极性分子
D.以上说明都不对
2.科学家发现铂的两种化合物其化学式都为PtCl2(NH3)2,且均为平面正方形结构,但一种为黄绿色,在水中溶解度较大,具有抗癌作用,另一种为淡黄色,在水中溶解度较小,不具有抗癌作用。试回答下列问题:
(1)一这两种铂的化合物的几何构型图。
黄绿色:______________;淡黄色:______________。
(2)黄绿色固体在水中溶解度大的原因是__________________________。
思维方法: 。
展望高考: 。
[针对训练]
A.基础训练
7.相似相溶原理: 。
.[例题解析]
[例1] ] 氰(CN)2为无色可燃气体、剧毒、有苦杏仁味,和卤素单质的性质相似。
(1)写出氰与苛性钠溶液反应的离子方程式:_______________________。
(2)已知氰分子键之间夹角为180°并有对称性,(CN)2的电子式为______________,结构式为______________,(CN)2分子为______________(填“极性”或“非极性”)分子。
(3)CN-中电子数为______________,CN-的电子式为______________。
解题思路: 。
易错点: 。
[例2] 将下列粒子的符号填入相应的空格内:O2、NH3、CO2、H2O、N2、(NH4)2SO4、SiCl4。
(1)存在极性键的极性分子是______________。
(2)存在非极性键的非极性分子是______________。
(3)存在极性键的非极性分子是______________。
(4)全部由非金属元素组成的离子化合物是______________。
解题思路: 。
易错点: 。
[考题再现]1. 今有三种物质AC2、B2C2、AD4,元素A的最高正价和负价绝对值相等;元素B的单质能在C的气态单质中剧烈燃烧,火焰呈黄色,并生成淡黄色固体B2C2;元素D的负一价阴离子电子层结构与氩原子相同,则
(1)A、B、C、D的元素符号分别为_______________、_______________、____________、______________________。
(2)AC2的空间构型为______________,属______________分子,AD4的空间构型为______________,属______________分子。
(3)B2C2的电子式为__________,属_________ 。(填离子或共价化合物)
思维方法: 。
展望高考:
6.氢键:
(1)概念: 。
(2)形成条件: 。
(3)对物质性质的影响: 。
5.分子间作用力:
(1)概念: 。
(2)影响因素: 。
(3)对物质性的影响: 。
4.非极性分子:
(1)含义: 。
(2)判断方法:①根据键角判断分子中的正负电荷重心是否重叠
②根据ABn的中心原子A周围是否为完全等价的电子对
③根据ABn的中心原子A的最外层价电子是否全部参与形成
了同样的共价键。(或A是否达最高价)
(3)常见ABn型分子中极性分子与非极性分子比较:
分子类型 举例 键角 构形 分子极性
AB CO
AB2(A2B) H2O
CS2
BeCl2
AB3 PCl3
BF3
SO3
AB4 CH4
AB2C2 CH2Cl2
A2B4 C2H4
A2B2 C2H2
A6B6 C6H6
3.极性分子:
(1)含义: 。
(2)举例: 。
2.极性键:
(1)概念: 。
(2)形成条件: 。
(3)共价键极性强弱比较依据:形成共价键的共用电子对偏向与偏离程度越
大,键的极性就越强。试比较下列两组共价键的强弱:
①H-H、H-F、H-O、H-N、H-C: ;
②H-F、C-F、N-F、O-F、F-F: 。
1.非极性键:
(1)概念: 。
(2)形成条件: 。
25、(福建省莆田一中2007-2008学年上学期期末考试卷)在平面直角坐标系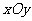 中,过定点
中,过定点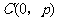 作直线与抛物线
作直线与抛物线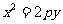 (
(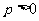 )相交于
)相交于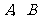 两点.
两点.
(I)若点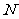 是点
是点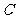 关于坐标原点
关于坐标原点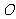 的对称点,求
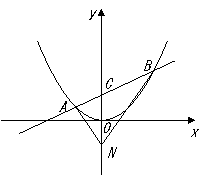
的对称点,求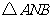 面积的最小值;
面积的最小值;
(II)是否存在垂直于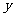 轴的直线
轴的直线 ,使得
,使得 被以
被以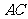 为直径的圆截得的弦长恒为定值?若存在,求出
为直径的圆截得的弦长恒为定值?若存在,求出 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
解法1:(Ⅰ)依题意,点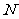 的坐标为
的坐标为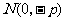 ,可设
,可设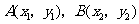 ,
,
直线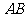 的方程为
的方程为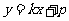 ,与
,与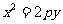 联立得
联立得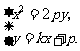 消去
消去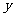 得
得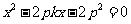 .
.
由韦达定理得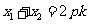 ,
, .
.
 于是
于是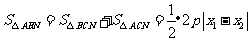 .
.
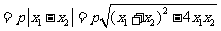
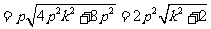 ,
,
 当
当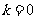 时,
时,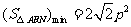 .
.
(Ⅱ)假设满足条件的直线 存在,其方程为
存在,其方程为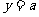 ,
,
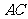 的中点为
的中点为 ,
, 与
与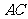 为直径的圆相交于点
为直径的圆相交于点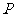 ,
,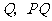 的中点为
的中点为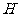 ,
,
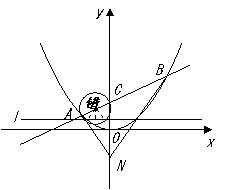 则
则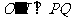 ,
, 点的坐标为
点的坐标为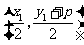 .
.
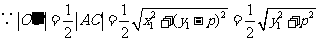 ,
,
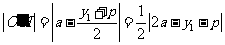 ,
,
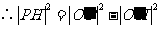
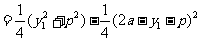
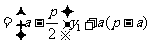 ,
,
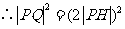
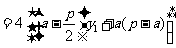 .
.
令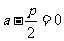 ,得
,得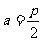 ,此时
,此时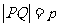 为定值,故满足条件的直线
为定值,故满足条件的直线 存在,其方程为
存在,其方程为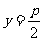 ,
,
即抛物线的通径所在的直线.
解法2:(Ⅰ)前同解法1,再由弦长公式得
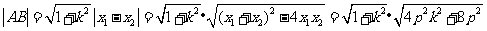
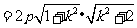 ,
,
又由点到直线的距离公式得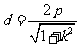 .
.
从而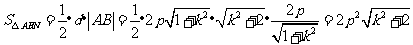 ,
,
 当
当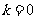 时,
时,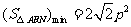 .
.
(Ⅱ)假设满足条件的直线 存在,其方程为
存在,其方程为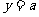 ,则以
,则以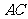 为直径的圆的方程为
为直径的圆的方程为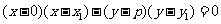 ,
,
将直线方程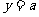 代入得
代入得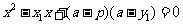 ,
,
则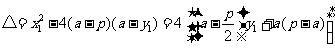 .
.
设直线 与以
与以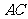 为直径的圆的交点为
为直径的圆的交点为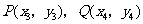 ,
,
则有 .
.
令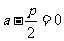 ,得
,得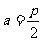 ,此时
,此时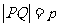 为定值,故满足条件的直线
为定值,故满足条件的直线 存在,其方程为
存在,其方程为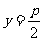 ,
,
即抛物线的通径所在的直线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com