
11. ; 12. ;
7. ; 8. ; 9. ; 10. ;
5. ; 6. ;
3. ; 4. ;
1. ; 2. ;
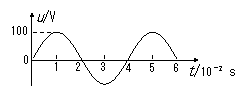
1]一正弦交流电的电压随时间变化的规律如图所示.由图可知( )
A.该交流电的电压瞬时值的表达式为u=100sin(25t)V
B.该交流电的频率为25 Hz
C.该交流电的电压的有效值为100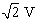

D.若将该交流电压加在阻值R=100 Ω的电阻两端,则电阻消耗的功率为50 W



 [2]将阻值为5Ω的电阻接到内阻不计的交流电源上,电源电动势随时间变化的规律如图所示.下列说法正确的是
( )
[2]将阻值为5Ω的电阻接到内阻不计的交流电源上,电源电动势随时间变化的规律如图所示.下列说法正确的是
( )
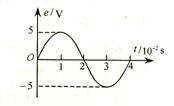 A.电路中交变电流的频率为0.25 Hz
A.电路中交变电流的频率为0.25 Hz
B.通过电阻的电流为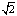 A
A
C.电阻消耗的电功率为2.5 W
D.用交流电压表测得电阻两端的电压是5 V

 [3]
如图所示,理想变压器原、副线圈匝数之比为20∶1,原线圈接正弦交流电,副线圈接入“220V,60W”灯泡一只,且灯泡正常发光.则 ( )
[3]
如图所示,理想变压器原、副线圈匝数之比为20∶1,原线圈接正弦交流电,副线圈接入“220V,60W”灯泡一只,且灯泡正常发光.则 ( )
 A.电流表的示数为
A.电流表的示数为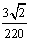 A
A 
B.电源输出功率为1200W
C.电流表的示数为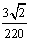 A
A 
D.原线圈端电压为11V
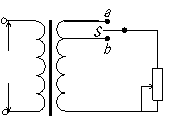
 [4] 如图所示电路中的变压器为理想变压器,S为单刀双掷开关.P是滑动变阻器R的滑动触头,U1 为加在原线圈两端的交变电压,I1、I2 分别为原线圈和副线圈中的电流.下列说法正确的是 ( )
[4] 如图所示电路中的变压器为理想变压器,S为单刀双掷开关.P是滑动变阻器R的滑动触头,U1 为加在原线圈两端的交变电压,I1、I2 分别为原线圈和副线圈中的电流.下列说法正确的是 ( )
A.保持P的位置及U1不变,S由b切换到a,则R上消耗的功率减小
B.保持P的位置及U1不变,S由a切换到b,则I2减小
C.保持P的位置及U1 不变,S由b切换到a,则I1增大 
 D.保持U1不变,S接在b端,将P向上滑动,则 I1减小
D.保持U1不变,S接在b端,将P向上滑动,则 I1减小 





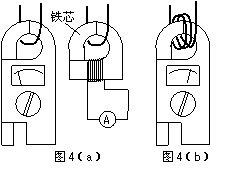
 [5]钳形电流表的外形和结构如图4(a)所示.图4(a)中电流表的读数为1.2A .图4(b)中用同一电缆线绕了3匝,则 (
)
[5]钳形电流表的外形和结构如图4(a)所示.图4(a)中电流表的读数为1.2A .图4(b)中用同一电缆线绕了3匝,则 (
)
A.这种电流表能测直流电流,图4(b)的读数为2.4A
B.这种电流表能测交流电流,图4(b)的读数为0.4A
C.这种电流表能测交流电流,图4(b)的读数为3.6A
D.这种电流表既能测直流电流,又能测交流电流,图4(b)的读数为3.6A 








 [6]如图所示,自耦变压器输入端A、B接交流稳压电源,其电压有效值UAB=100V,R0=40W,当滑动片处于线圈中点位置时,C、D两端电压的有效值UCD为___________V,通过电阻R0的电流有效值为_____________A.
[6]如图所示,自耦变压器输入端A、B接交流稳压电源,其电压有效值UAB=100V,R0=40W,当滑动片处于线圈中点位置时,C、D两端电压的有效值UCD为___________V,通过电阻R0的电流有效值为_____________A.
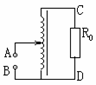



 [7] 如图所示,一理想变压器原、副线圈匝数分别为nl和n2, 当负载电阻R中流过的电流为I时,原线圈中流过的电流为 ;现减小负载电阻R的阻值,则变压器的输入功率将
(填“增大”、“减小”或“不变”).
[7] 如图所示,一理想变压器原、副线圈匝数分别为nl和n2, 当负载电阻R中流过的电流为I时,原线圈中流过的电流为 ;现减小负载电阻R的阻值,则变压器的输入功率将
(填“增大”、“减小”或“不变”).
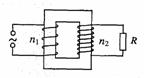




 [8]某发电站的输出功率为
[8]某发电站的输出功率为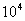 kW,输出电压为4kV,通过理想变压器升压后向80km远处供电.已知输电导线的电阻率为
kW,输出电压为4kV,通过理想变压器升压后向80km远处供电.已知输电导线的电阻率为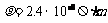 ,导线横截面积为
,导线横截面积为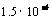 m2,输电线路损失的功率为输出功率的4%,求:
m2,输电线路损失的功率为输出功率的4%,求:
(1)升压变压器的输出电压;
(2)输电线路上的电压损失.


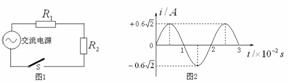
 [9]电阻R1、R2与交流电源按照图1方式连接,
[9]电阻R1、R2与交流电源按照图1方式连接,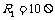 ,
,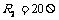 .合上开关S后,通过电阻
.合上开关S后,通过电阻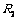 的正弦交变电流
的正弦交变电流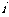 随时间
随时间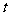 变化的情况如图2所示.则
变化的情况如图2所示.则 


A.通过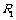 的电流有效值是
的电流有效值是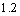 A
A

B.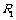 两端的电压有效值是6V
两端的电压有效值是6V
C.通过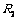 的电流最大值是
的电流最大值是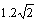 A
A 
D.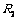 两端的电压最大值是
两端的电压最大值是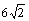 V
V
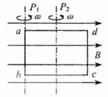
 [10]如图所示,矩形线圈abcd在匀强磁场中可以分别绕垂直于磁场方向的轴P1和P2以相同的角速度匀速转动,当线圈平面转到与磁场方向平行时
[10]如图所示,矩形线圈abcd在匀强磁场中可以分别绕垂直于磁场方向的轴P1和P2以相同的角速度匀速转动,当线圈平面转到与磁场方向平行时
A.线圈绕P1转动时的电流等于绕P2转动时的电流
B.线圈绕P1转动时的电动势小于绕P2转动时的电动势
C.线圈绕P1和P2转动时电流的方向相同,都是a→b→c→d
D 线圈绕P1转动时dc边受到的安培力大于绕P2转动时dc边受到的安培力
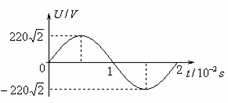
 [11]某变压器原、副线圈匝数比为55∶9,原线圈所接电源电压按图示规律变化,副线圈接有负载.下列判断正确的是
( )
[11]某变压器原、副线圈匝数比为55∶9,原线圈所接电源电压按图示规律变化,副线圈接有负载.下列判断正确的是
( )
A.输出电压的最大值为36V
B.原、副线圈中电流之比为55∶9
C.变压器输入、输出功率之比为55∶9
D.交流电源有效值为220V,频率为50Hz
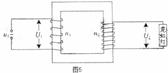
 [12]图5是霓虹灯的供电电路,电路中的变压器可视为理想变压器,已知变压器原线圈与副线圈匝数比
[12]图5是霓虹灯的供电电路,电路中的变压器可视为理想变压器,已知变压器原线圈与副线圈匝数比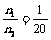 ,加在原线圈的电压为
,加在原线圈的电压为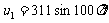 (V),霓虹灯正常工作的电阻R=440kΩ,I1、I2表示原、副线圈中的电流,下列判断正确的是 ( )
(V),霓虹灯正常工作的电阻R=440kΩ,I1、I2表示原、副线圈中的电流,下列判断正确的是 ( )
A.副线圈两端电压6220V,副线圈中的电流14.1mA
B.副线圈两端电压4400V,副线圈中的电流10.0mA
 C.I1<I2
C.I1<I2 
D.I1>I2


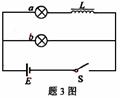
 [13]在如图所示的电路中,
[13]在如图所示的电路中, 、
、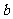 为两个完全相同的灯泡,
为两个完全相同的灯泡,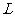 为自感线圈,
为自感线圈,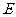 为电源,
为电源,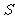 为开关,关于两灯泡点亮和熄灭的先后次序,下列说法正确的是 ( )
为开关,关于两灯泡点亮和熄灭的先后次序,下列说法正确的是 ( )
A.合上开关,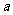 先亮,
先亮,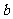 后亮;断开开关,
后亮;断开开关,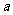 、
、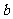 同时熄灭
同时熄灭 
B.合上开关,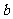 先亮,
先亮,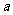 后亮;断开开关,
后亮;断开开关,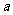 先熄灭,
先熄灭,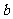 后熄灭
后熄灭
C.合上开关,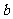 先亮,
先亮,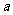 后亮;断开开关,
后亮;断开开关,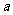 、
、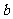 同时熄灭
同时熄灭
D.合上开关,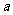 、
、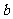 同时亮;断开开关,
同时亮;断开开关,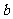 先熄灭,
先熄灭,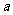 后熄灭
后熄灭
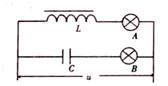
 [14] 如图所示L为电感线圈,C为电容,A、B为两只相同的灯泡,将他们接在电压为U的交流电源上,两灯泡的亮度相同,若保持电源电压不变,而将电源频率增大,下列关于两灯泡发光情况说法正确的是
( )
[14] 如图所示L为电感线圈,C为电容,A、B为两只相同的灯泡,将他们接在电压为U的交流电源上,两灯泡的亮度相同,若保持电源电压不变,而将电源频率增大,下列关于两灯泡发光情况说法正确的是
( )
 A.两灯泡亮度不变
A.两灯泡亮度不变
B.A灯泡亮度不变,B灯泡变亮
C.A灯泡变暗,B灯泡变亮
D.A灯泡变亮,B灯泡变暗
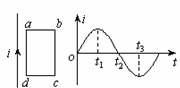
 [15]如图所示,长直导线右侧的矩形线框abcd与直导线位于同一平面,当长直导线中的电流发生如图所示的变化时(图中所示电流方向为正方向),线框中的感应电流与线框受力情况为
( )
[15]如图所示,长直导线右侧的矩形线框abcd与直导线位于同一平面,当长直导线中的电流发生如图所示的变化时(图中所示电流方向为正方向),线框中的感应电流与线框受力情况为
( )
A.t1到t2时间内,线框内电流的方向为abcda,线框受力向右
B.t1到t2时间内,线框内电流的方向为abcda,线框受力向左
C.在t2时刻,线框内电流的方向为abcda,线框受力向右
D.在t3时刻,线框内无电流,线框不受力
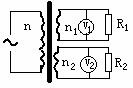
 [16]如图,一理想变压器,原线圈的匝数为
[16]如图,一理想变压器,原线圈的匝数为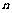 ,两个副线圈的匝数分别为
,两个副线圈的匝数分别为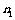 和
和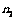 .变压器输入电压
.变压器输入电压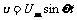 V,电压表V1和V2的读数分别为
V,电压表V1和V2的读数分别为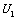 和
和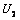 .变压器输入电流为
.变压器输入电流为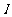 ,通过
,通过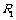 和
和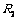 的电流分别为
的电流分别为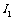 和
和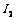 .变压器的输入功率为
.变压器的输入功率为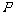 ,
,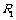 和
和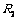 的电功率分别为
的电功率分别为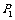 和
和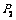 .则下列式子正确的是( )
.则下列式子正确的是( )
A.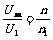 ;
;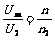
B.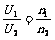 .
.
C.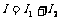 .
.
D.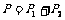
 [17]理想变压器的原线圈连接电流表,副线圈接入电路的匝数可以通过触头Q调节,在副线圈输出端连接了定值电阻R0和滑动变阻器R,在原线圈上加一电压为U的交流电,如图所示,若( )
[17]理想变压器的原线圈连接电流表,副线圈接入电路的匝数可以通过触头Q调节,在副线圈输出端连接了定值电阻R0和滑动变阻器R,在原线圈上加一电压为U的交流电,如图所示,若( )
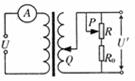 A.Q位置不变,将P向上滑动,U′变大
A.Q位置不变,将P向上滑动,U′变大
B.Q位置不变,将P向上滑动,电流表的读数变大
C.P位置不变,将Q向上滑动,电流表的读数变大
D.P位置不变,将Q向上滑动,变压器的输入功率不变

86、
85、(上海市部分重点中学2008届高三第二次联考)设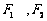 分别是椭圆C:
分别是椭圆C: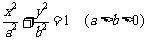 的左右焦点
的左右焦点
(1)设椭圆C上的点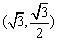 到
到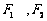 两点距离之和等于4,写出椭圆C的方程和焦点坐标
两点距离之和等于4,写出椭圆C的方程和焦点坐标
(2)设K是(1)中所得椭圆上的动点,求线段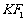 的中点B的轨迹方程
的中点B的轨迹方程
(3)设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为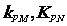 试探究
试探究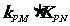 的值是否与点P及直线L有关,并证明你的结论。
的值是否与点P及直线L有关,并证明你的结论。
[解]:(1)由于点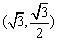 在椭圆上,
在椭圆上, ------1分
------1分
2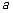 =4,
------2分
=4,
------2分
椭圆C的方程为 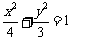 --------3分
--------3分
焦点坐标分别为(-1,0) ,(1,0)-----------4分
(2)设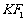 的中点为B(x, y)则点
的中点为B(x, y)则点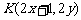 --------6分
--------6分
把K的坐标代入椭圆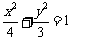 中得
中得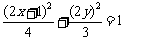 -----8分
-----8分
线段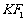 的中点B的轨迹方程为
的中点B的轨迹方程为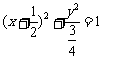 ----------10分
----------10分
(3)过原点的直线L与椭圆相交的两点M,N关于坐标原点对称
设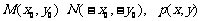 ----11分
----11分
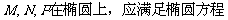 ,得
,得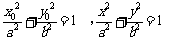 ------12分
------12分
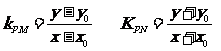 -------------------13分
-------------------13分
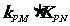 =
=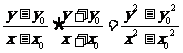 =
=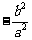 -----------15分
-----------15分
故: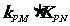 的值与点P的位置无关,同时与直线L无关,-----16分
的值与点P的位置无关,同时与直线L无关,-----16分
84、(山西大学附中2008届二月月考)已知曲线C上任意一点M到点F(0,1)的距离比它到直线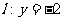 的距离小1.
的距离小1.
(1)求曲线C的方程;
(2)过点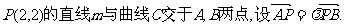 当△AOB的面积为4时(O为坐标原点),求
当△AOB的面积为4时(O为坐标原点),求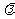 的值.
的值.
解:(1) 的距离小于1,
的距离小于1,
∴点M在直线l的上方,点M到F(1,0)的距离与它到直线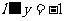 的距离相等
的距离相等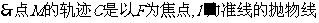 ,所以曲线C的方程为
,所以曲线C的方程为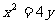
(2)当直线m的斜率不存在时,它与曲线C只有一个交点,不合题意,
设直线m的方程为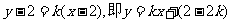 ,
,
代入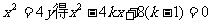 (*)
(*)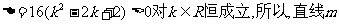 与曲线C恒有两个不同的交点 设交点A,B的坐标分别为
与曲线C恒有两个不同的交点 设交点A,B的坐标分别为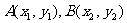 ,
,
则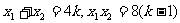
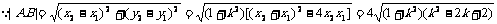
点O到直线m的距离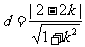 ,
,
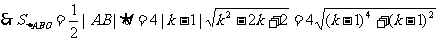
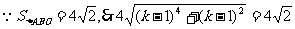 ,
,
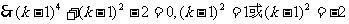 (舍去)
(舍去)
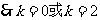
当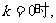 方程(*)的解为
方程(*)的解为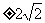 若
若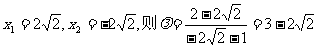
若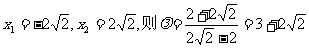 当
当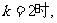 方程(☆)的解为
方程(☆)的解为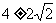
若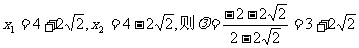
若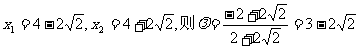 所以,
所以,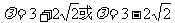
83、(山东省实验中学2008届高三第三次诊断性测试)已知椭圆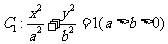 的离心率为,直线
的离心率为,直线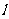 :
: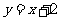 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆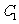 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(1)求椭圆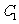 的方程;
的方程;
(2)设椭圆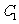 的左焦点为
的左焦点为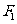 ,右焦点
,右焦点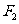 ,直线
,直线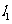 过点
过点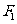 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线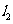 垂直
垂直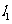 于点
于点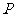 ,线段
,线段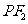 垂直平分线交
垂直平分线交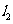 于点
于点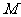 ,求点
,求点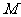 的轨迹
的轨迹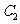 的方程;
的方程;
(3)设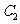 与
与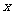 轴交于点
轴交于点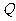 ,不同的两点
,不同的两点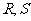 在
在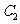 上,且满足
上,且满足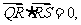 求
求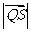 的取值范围.
的取值范围.
解:(Ⅰ)∵ ……1分
……1分
∵直线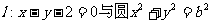 相切,
相切,
∴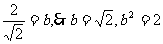 …………2分
…………2分
∴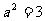 …………3分
…………3分
∵椭圆C1的方程是 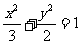 ………………4分
………………4分
(Ⅱ)∵MP=MF2,
∴动点M到定直线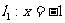 的距离等于它到定点F1(1,0)的距离,
的距离等于它到定点F1(1,0)的距离,
∴动点M的轨迹是C为l1准线,F2为焦点的抛物线 ………………6分
∴点M的轨迹C2的方程为 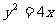 …………7分
…………7分
(Ⅲ)Q(0,0),设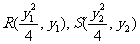 …………8分
…………8分
∴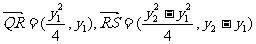 …………9分
…………9分
∵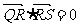
∴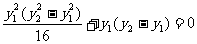
∵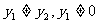 ,化简得
,化简得
∴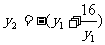 ………………11分
………………11分
∴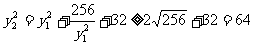
当且仅当 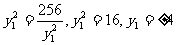 时等号成立 …………13分
时等号成立 …………13分
∵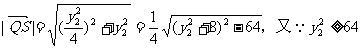
∴当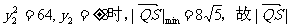 的取值范围是
的取值范围是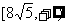 ……14分
……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com