
2、 (常州)已知
(常州)已知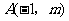 与
与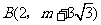 是反比例函数
是反比例函数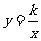 图象上的两个点.
图象上的两个点.
(1)求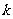 的值;
的值;
(2)若点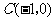 ,则在反比例函数
,则在反比例函数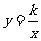 图象上是否存在点
图象上是否存在点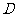 ,使得以
,使得以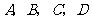 四点为顶点的四边形为梯形?若存在,求出点
四点为顶点的四边形为梯形?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
解:(1)由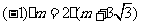 ,得
,得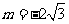 ,因此
,因此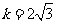 .······ 2分
.······ 2分
(2)如图1,作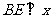 轴,
轴,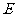 为垂足,则
为垂足,则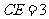 ,
,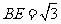 ,
,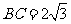 ,因此
,因此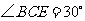 .
.
由于点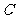 与点
与点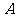 的横坐标相同,因此
的横坐标相同,因此 轴,从而
轴,从而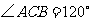 .
.
当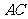 为底时,由于过点
为底时,由于过点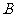 且平行于
且平行于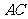 的直线与双曲线只有一个公共点
的直线与双曲线只有一个公共点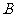 ,
,
故不符题意.······························ 3分
当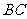 为底时,过点
为底时,过点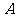 作
作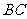 的平行线,交双曲线于点
的平行线,交双曲线于点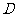 ,
,
过点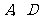 分别作
分别作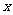 轴,
轴,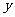 轴的平行线,交于点
轴的平行线,交于点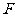 .
.
由于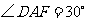 ,设
,设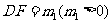 ,则
,则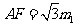 ,
,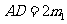 ,
,
由点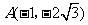 ,得点
,得点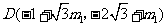 .
.
因此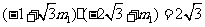 ,
,
解之得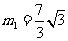 (
(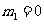 舍去),因此点
舍去),因此点 .
.

 此时
此时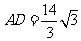 ,与
,与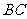 的长度不等,故四边形
的长度不等,故四边形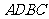 是梯形.······· 5分
是梯形.······· 5分
如图2,当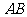 为底时,过点
为底时,过点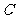 作
作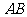 的平行线,与双曲线在第一象限内的交点为
的平行线,与双曲线在第一象限内的交点为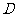 .
.
由于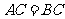 ,因此
,因此 ,从而
,从而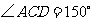 .作
.作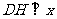 轴,
轴,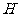 为垂足,
为垂足,
则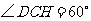 ,设
,设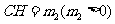 ,则
,则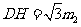 ,
,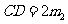
由点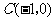 ,得点
,得点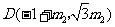 ,
,
因此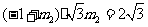 .
.
解之得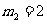 (
(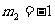 舍去),因此点
舍去),因此点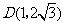 .
.
此时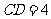 ,与
,与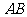 的长度不相等,故四边形
的长度不相等,故四边形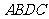 是梯形.········· 7分
是梯形.········· 7分
如图3,当过点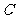 作
作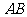 的平行线,与双曲线在第三象限内的交点为
的平行线,与双曲线在第三象限内的交点为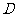 时,
时,
同理可得,点 ,四边形
,四边形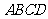 是梯形.·············· 9分
是梯形.·············· 9分
 综上所述,函数
综上所述,函数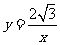 图象上存在点
图象上存在点 ,使得以
,使得以 四点为顶点的四边形为梯形,点
四点为顶点的四边形为梯形,点 的坐标为:
的坐标为: 或
或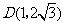 或
或 .··················· 10分
.··················· 10分
1、 (安徽)按右图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20-100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(安徽)按右图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20-100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(Ⅰ)新数据都在60-100(含60和100)之间;
(Ⅱ)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大。
(1)若y与x的关系是y=x+p(100-x),请说明:当p=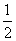 时,这种变换满足上述两个要求;
时,这种变换满足上述两个要求;
(2)若按关系式y=a(x-h)2+k (a>0)将数据进行变换,请写出一个满足上述要求的这种关系式。(不要求对关系式符合题意作说明,但要写出关系式得出的主要过程)
[解](1)当P=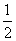 时,y=x+
时,y=x+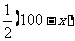 ,即y=
,即y=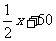 。
。
∴y随着x的增大而增大,即P=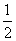 时,满足条件(Ⅱ)……3分
时,满足条件(Ⅱ)……3分
又当x=20时,y=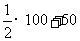 =100。而原数据都在20-100之间,所以新数据都在60-100之间,即满足条件(Ⅰ),综上可知,当P=
=100。而原数据都在20-100之间,所以新数据都在60-100之间,即满足条件(Ⅰ),综上可知,当P=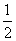 时,这种变换满足要求;……6分
时,这种变换满足要求;……6分
(2)本题是开放性问题,答案不唯一。若所给出的关系式满足:(a)h≤20;(b)若x=20,100时,y的对应值m,n能落在60-100之间,则这样的关系式都符合要求。
如取h=20,y=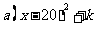 ,……8分
,……8分
∵a>0,∴当20≤x≤100时,y随着x的增大…10分
令x=20,y=60,得k=60 ①
令x=100,y=100,得a×802+k=100 ②
由①②解得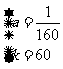 , ∴
, ∴ 。………14分
。………14分
3.(2010年全国理13)设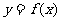 为区间
为区间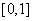 上的连续函数,且恒有
上的连续函数,且恒有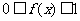 ,可以用随机模拟方法近似计算积分
,可以用随机模拟方法近似计算积分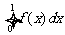 ,先产生两组(每组N个)区间
,先产生两组(每组N个)区间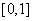 上的均匀随机数
上的均匀随机数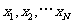 和
和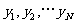 ,由此得到N个点
,由此得到N个点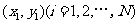 ,再数出其中满足
,再数出其中满足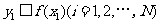 的点数
的点数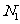 ,那么由随机模拟方案可得积分
,那么由随机模拟方案可得积分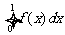 的近似值为 。
的近似值为 。
[答案]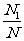 解析:
解析: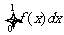 的几何意义是函数
的几何意义是函数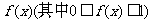 的图像与
的图像与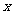 轴、直线
轴、直线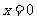 和直线
和直线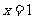 所围成图形的面积,根据几何概型易知
所围成图形的面积,根据几何概型易知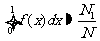 .
.
2.( 2010年陕西理13).从如图所示的长方形区域内任取一个点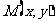 ,则点
,则点 取自阴影部分的概率为
取自阴影部分的概率为 .
.
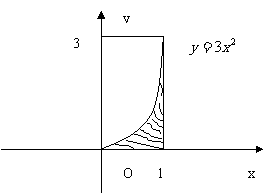
[解析]本题属于几何概型求概率,∵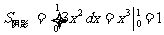 ,
,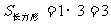 ,∴所求概率为
,∴所求概率为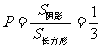 .
.
1.(2008年山东理14)设函数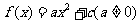 ,若
,若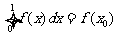 ,
,
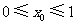 ,则
,则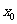 的值为
.
的值为
.
解: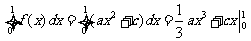
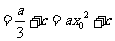
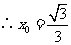
4.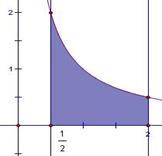 (2008年海南理10)由直线
(2008年海南理10)由直线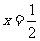 ,x=2,曲线
,x=2,曲线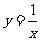 及x轴所围图形的面积为( )
及x轴所围图形的面积为( )
A.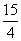 B.
B.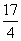 C.
C.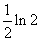 D.
D.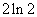
D解:如图,面积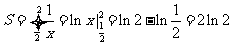
3.(2009年福建理4) 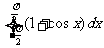 等于
等于
A.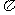 B. 2
C.
B. 2
C. 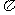 -2
D.
-2
D. 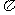 +2
+2
[答案]:D[解析]∵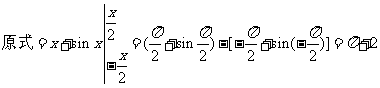 .故选D
.故选D
2.( 2010年山东理7)由曲线y=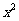 ,y=
,y=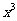 围成的封闭图形面积为
围成的封闭图形面积为
(A)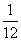 (B)
(B)
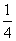 (C)
(C) 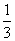 (D)
(D)
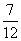
[答案]A[解析]由题意得:所求封闭图形的面积为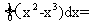
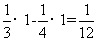 ,故选A。
,故选A。
[命题意图]本题考查定积分的基础知识,由定积分求曲线围成封闭图形的面积。
1.( 2010年湖南理5)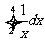 等于( )
等于( )
A、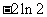 B、
B、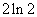 C、
C、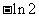 D、
D、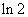
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com