
1.交集的定义
一般地,由所有属于A且属于B的元素所组成的集合,叫做A,B的交集.
记作A B(读作‘A交B’),即A
B(读作‘A交B’),即A B={x|x
B={x|x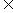 A,且x
A,且x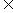 B}.
B}.
11. ⑴设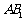 和
和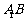 的交点为
的交点为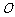 ,连接
,连接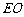 ,连接
,连接 ,
,

因为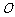 为
为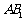 的中点,
的中点,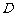 为
为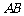 的中点,
的中点,
所以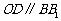 ,且
,且 又
又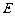 是
是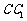 中点,
中点,
则 且
且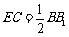 ,
,
所以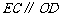 且
且 .
.
所以四边形 为平行四边形,
为平行四边形,
所以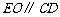 .
.
又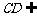 平面
平面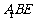 ,
,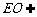 平面
平面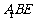 ,
,
则 平面
平面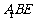 ……………………5分
……………………5分
⑵因为三棱柱各侧面都是正方形,
所以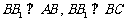 ,
,
所以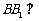 平面
平面 .
.
因为 平面
平面 ,所以
,所以 .
.
由已知得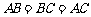 ,
,
所以 .
.
所以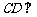 平面
平面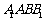
由⑴可知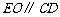 ,
,
所以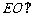 平面
平面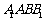 .
.
所以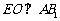 .
.
因为侧面是正方形,所以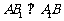 .
.
又 平面
平面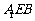 ,
,
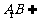 平面
平面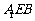 .
.
所以 平面
平面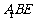 .
.
⑶取 中点
中点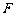 ,连接
,连接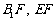 .
.
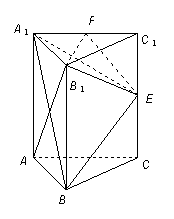
在三棱柱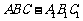 中,
中,
因为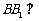 平面
平面
所以侧面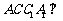 底面
底面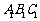 .
.
因为底面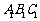 是正三角形,且
是正三角形,且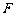 是
是 中点,
中点,
所以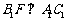 ,所以
,所以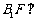 侧面
侧面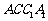 .
.
所以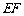 是
是 在平面
在平面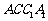 上的射影,
上的射影,
所以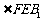 是
是 与平面
与平面 所成角.
所成角.
 . ………………14分
. ………………14分
解法二:如图所示,建立空间直角坐标系.

设边长为2,可求得 ,
,
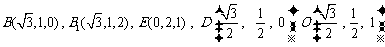 .
.
⑴易知,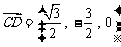 ,
,
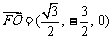 ,所以
,所以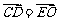 ,所以
,所以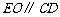 .
.
又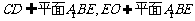 ,则
,则 平面
平面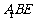 …………5分
…………5分
⑵易得,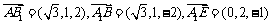
所以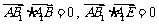 .
.
所以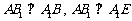 .
.
又因为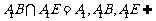 平面
平面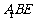 .
.
所以 平面
平面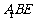 .………………10分
.………………10分
⑶设侧面 的法向量为
的法向量为 .
.
因为 .
.
所以 .
.
由 得
得 解得
解得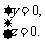 .
.
不妨令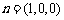 ,设直线
,设直线 与平面
与平面 所成角为
所成角为 ,
,
所以 .
.
所以直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为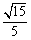 .
.
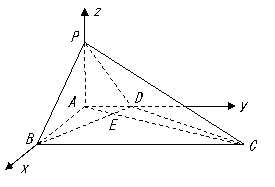
10. 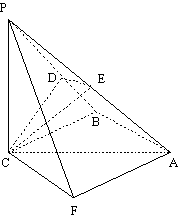 解法一(1)∵PC
解法一(1)∵PC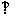 平面ABC,
平面ABC,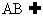 平面ABC,∴PC
平面ABC,∴PC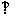 AB.……(2分)
AB.……(2分)
∵CD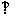 平面PAB,
平面PAB,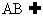 平面PAB,∴CD
平面PAB,∴CD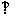 AB.……………(3分)
AB.……………(3分)
又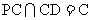 ,∴AB
,∴AB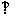 平面PCB.
……………………(4分)
平面PCB.
……………………(4分)
(2)过点A作AF//BC,且AF=BC,连结PF,CF.
则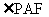 为异面直线PA与BC所成的角.………(6分)
为异面直线PA与BC所成的角.………(6分)
由(1)可得AB⊥BC,∴CF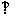 AF.
AF.
由三垂线定理,得PF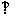 AF.
AF.
则AF=CF=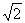 ,PF=
,PF= ,
,
在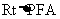 中, tan∠PAF=
中, tan∠PAF= =
= ,
,
∴异面直线PA与BC所成的角为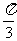 .…………………………………(8分)
.…………………………………(8分)
(3)取AP的中点E,连结CE、DE.
∵PC=AC=2,∴CE 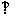 PA,CE=
PA,CE=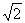 .
.
∵CD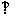 平面PAB,
平面PAB,
由三垂线定理的逆定理,得
DE 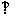 PA.
PA.
∴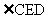 为二面角C-PA-B的平面角.…………………………………(10分)
为二面角C-PA-B的平面角.…………………………………(10分)
由(1) AB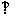 平面PCB,又∵AB=BC,可得BC=
平面PCB,又∵AB=BC,可得BC=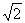 .
.
在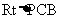 中,PB=
中,PB=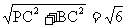 ,
,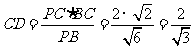 .
.
在 中,
中,
sin∠CED=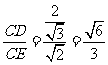 .
.  ……(12分)
……(12分)
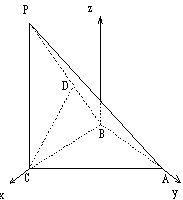 解法二:(1)同解法一.
解法二:(1)同解法一.
(2)
由(1) AB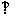 平面PCB,∵PC=AC=2,
平面PCB,∵PC=AC=2,
又∵AB=BC,可求得BC=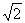 .
.
以B为原点,如图建立坐标系.
则A(0,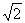 ,0),B(0,0,0),
,0),B(0,0,0),
C(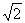 ,0,0),P(
,0,0),P(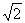 ,0,2).
,0,2).
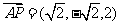 ,
,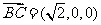 .
.
…………………(7分)
则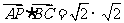 +0+0=2.
+0+0=2.
 =
=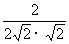 =
=
 .
.
∴异面直线AP与BC所成的角为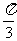 .………………………(8分)
.………………………(8分)
(3)设平面PAB的法向量为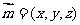 .
.
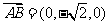 ,
,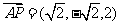 ,
,
则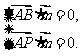 即
即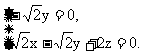
 解得
解得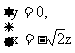 令
令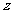 = -1, 得
= -1, 得 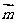 = (
= (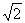 ,0,-1).
,0,-1).
设平面PAC的法向量为 =(
=(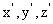 ).
).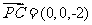 ,
,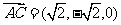 ,
,
则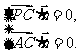 即
即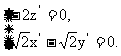 解得
解得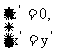 令
令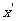 =1, 得 n= (1,1,0).
=1, 得 n= (1,1,0).
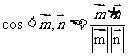 =
=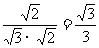 .………………(12分)
.………………(12分)
9. (Ⅰ)证明: ,
,

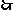 面
面 面
面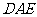 .
.
又 面
面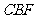 ,
,
所以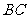
 平面
平面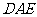 .
.
(Ⅱ)取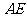 的中点
的中点 ,连接
,连接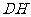 .
.
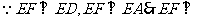 平面
平面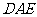
又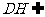 平面
平面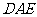
 .
.
 ,
,
 面
面 .
.
所以四棱锥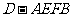 的体积
的体积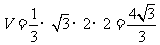 .
.
(Ⅲ)如图以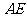 中点为原点,
中点为原点,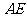 为
为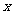 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
则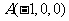 ,
, ,
,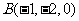 ,
,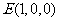
所以 的中点坐标为
的中点坐标为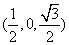 .
.
因为 ,所以
,所以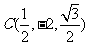 .
.
易知 是平面
是平面 的一个法向量,
的一个法向量,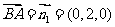 .
.
设平面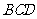 的一个法向量为
的一个法向量为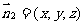
由
令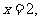 则
则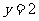 ,
,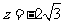 ,
,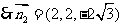 .
.
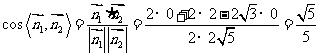 .
.
所以面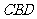 与面
与面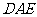 所成锐二面角的余弦值为
所成锐二面角的余弦值为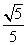 .
.
18.8. 解:(I)证明: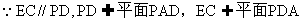 ,
,
 ,同理可得BC//平面PDA,
,同理可得BC//平面PDA,

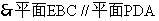
又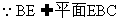 ,
,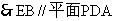 …………………………………………4分
…………………………………………4分
(II)如图以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系如图示:设该简单组合体的底面边长为1,PD=a,
则B(1,1,0),C(0,1,0),P(0,0,a),E(0,1,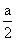 ),N(
),N( ,
, ,
,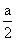 )。
)。
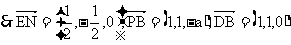

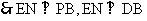
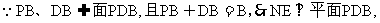 ……………………8分
……………………8分
(III)连结DN,由(II)知

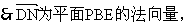
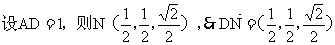
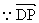 为平面ABCD的法向量,
为平面ABCD的法向量,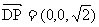 ,
,
设平面PBE与平面ABCD所成的二面角为 ,则
,则
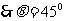 ,即平面PBE与平面ABCD所成的二面角为450………………………13分
,即平面PBE与平面ABCD所成的二面角为450………………………13分
7. ⑴∵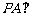 面
面 ,四边形
,四边形 是正方形,其对角线
是正方形,其对角线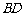 ,
, 交于点
交于点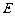 ,
,
∴ ,
,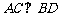 .
.
∴ 平面
平面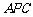 ,
,
∵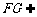 平面
平面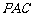 ,
,
∴
⑵当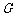 为
为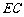 中点,即
中点,即 时,
时,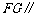 平面
平面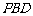 ,理由如下:
,理由如下:
连结 ,由
,由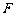 为
为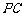 中点,
中点,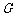 为
为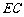 中点,知
中点,知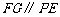 ,
,
而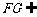 平面
平面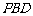 ,
, 平面
平面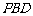 ,
,
故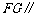 平面
平面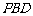 .
.
⑶作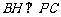 于
于 ,连结
,连结 ,
,
∵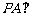 面
面 ,四边形
,四边形 是正方形,
是正方形,
∴ ,
,
又∵ ,
, ,∴
,∴ ,
,
∴ ,且
,且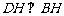 ,
,
∴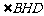 是二面角
是二面角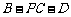 的平面角,
的平面角,
即 ,
,
∵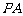 ⊥面
⊥面 ,∴
,∴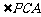 就是
就是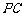 与底面
与底面 所成的角
所成的角
连结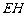 ,则
,则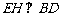 ,
,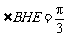 ,
,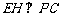
∴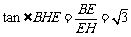 ,
,
∴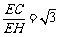 ,∴
,∴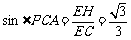 ,
,
∴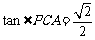
∴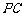 与底面
与底面 所成角的正切值是
所成角的正切值是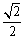 .
.
另解:以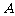 为原点,
为原点,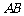 、
、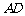 、
、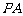 所在的直线分别为
所在的直线分别为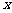 、
、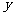 、
、 轴建立空间直角坐标系如图所示,
轴建立空间直角坐标系如图所示,
设正方形 的边长为
的边长为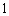 ,则
,则 ,
,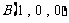 ,
,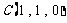 ,
,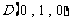 ,
,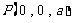
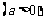 ,
, ,
, ,
,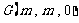
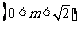 .
.
⑴ ,
,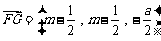 ,
,
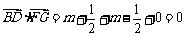
∴
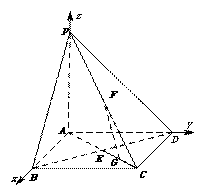
⑵要使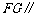 平面
平面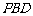 ,只需
,只需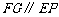 ,而
,而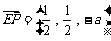 ,
,
由 可得
可得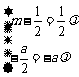 ,解得
,解得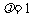 ,
,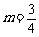 ,
,
∴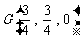 ,∴
,∴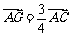
故当 时,
时,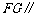 平面
平面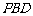
设平面 的一个法向量为
的一个法向量为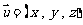 ,
,
则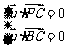 ,而
,而
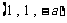 ,
, ,
,
∴ ,取
,取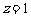 ,得
,得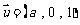 ,
,
同理可得平面 的一个法向量
的一个法向量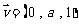
设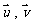 所成的角为
所成的角为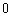 ,则
,则 ,
,
即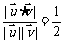 ,∴
,∴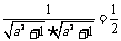 ,∴
,∴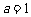
∵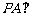 面
面 ,∴
,∴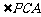 就是
就是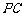 与底面
与底面 所成的角,
所成的角,
∴ .
.
6. (Ⅰ)证明:∵三棱柱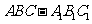 是直棱柱,∴
是直棱柱,∴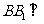 平面
平面 .
.
又∵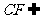 平面
平面 ,∴
,∴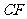
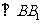 .
.
∵ ,
,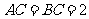 ,
, 是
是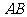 中点,∴
中点,∴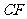
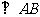 .
.
又∵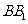 ∩
∩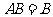 , ∴
, ∴ 平面
平面 .
.
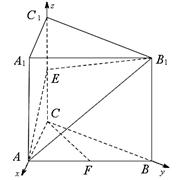 (Ⅱ)解:以
(Ⅱ)解:以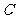 为坐标原点,射线
为坐标原点,射线 为
为 轴正半轴,建立如图所示的空间直角坐标系
轴正半轴,建立如图所示的空间直角坐标系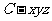 ,
,
则 ,
,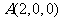 ,
, .
.
设 ,平面
,平面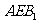 的法向量
的法向量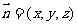 ,
,
则 ,
,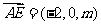 .
.
且 ,
,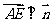 .于是
.于是
所以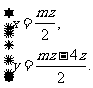 取
取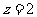 ,则
,则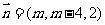
∵ 三棱柱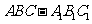 是直棱柱,∴
是直棱柱,∴
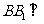 平面
平面 .又∵
.又∵
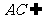 平面
平面 ,
,
∴ 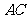
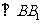 .∵
.∵  ,∴
,∴
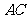
 .∵
.∵ 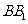 ∩
∩ ,
,
∴ 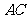
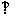 平面
平面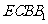 .∴
.∴ 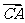 是平面
是平面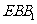 的法向量,
的法向量,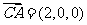 .
.
∵二面角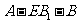 的大小是
的大小是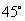 ,
,
∴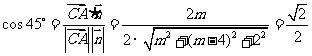 . 解得
. 解得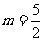 . ∴
. ∴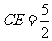 .
.
5. 解法一:(Ⅰ)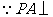 平面
平面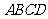 ,
,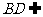 平面
平面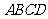 .
. .
.
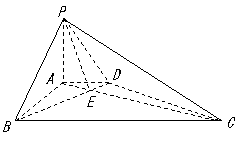 又
又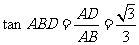 ,
,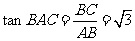 .
.
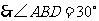 ,
, ,
,
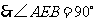 ,即
,即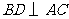 .
.
又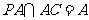 .
.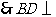 平面
平面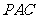 .
.
…………………..6分
(Ⅱ)连接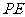 .
.
 平面
平面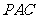 .
.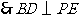 ,
,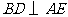 .
.
 为二面角
为二面角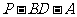 的平面角.
的平面角.
在 中,
中, ,
,
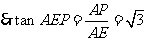 ,
, ,
,
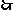 二面角
二面角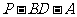 的大小为
的大小为 .
………………………..12分
.
………………………..12分
解法二:(Ⅰ)如图,建立坐标系,
则 ,
, ,
,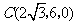 ,
,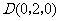 ,
, ,
,
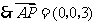 ,
,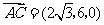 ,
,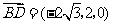 ,
,
 .
.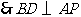 ,
,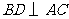 ,
,
又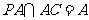 ,
,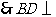 面
面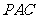 .
.
 (Ⅱ)设平面
(Ⅱ)设平面 的法向量为
的法向量为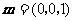 ,
,
设平面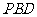 的法向量为
的法向量为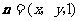 ,
,
则n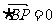 , n
, n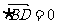
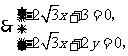 解得
解得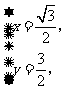
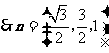 .
.
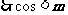 ,n>
,n>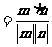
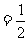 .
.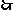 二面角
二面角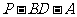 的大小为
的大小为 .
.
4. 方法1:(I)证明:∵平面PAD⊥平面ABCD,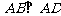 ,
,
∴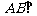 平面PAD,
…………(2分)
平面PAD,
…………(2分)
∵E、F为PA、PB的中点,
∴EF//AB,∴EF 平面PAD; …………(4分)
平面PAD; …………(4分)
(II)解:过P作AD的垂线,垂足为O,
∵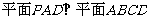 ,则PO
,则PO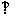 平面ABCD.
平面ABCD.
连OG,以OG,OD,OP为x、y、z轴建立空间坐标系,
…………(6分)
∵PA=PD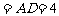 ,∴
,∴ ,
,
得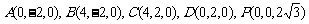 ,
,
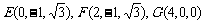 ,故
,故 ,
,
设平面EFG的一个法向量为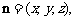 则
则 ,
,
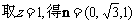 ,
…………(7分)
,
…………(7分)
平面ABCD的一个法向量为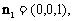
平面EFG与平面ABCD所成锐二面角的余弦值是:
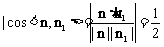 ,锐二面角的大小是
,锐二面角的大小是 ; …………(8分)
; …………(8分)
(III)解:设 ,M(x,
,M(x,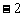 ,0),则
,0),则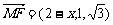 ,
,
设MF与平面EFG所成角为 ,
,
则 ,
,
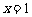 或
或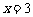 ,∵M靠近A,∴
,∵M靠近A,∴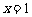 …………(10分)
…………(10分)
∴当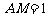 时, MF与平面EFG所成角正弦值等于
时, MF与平面EFG所成角正弦值等于 .………(12分)
.………(12分)
方法2:(I)证明:过P作P O AD于O,∵
AD于O,∵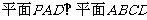 ,
,
则PO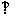 平面ABCD,连OG,以OG,OD,OP为x、y、z轴建立空间坐标系,
平面ABCD,连OG,以OG,OD,OP为x、y、z轴建立空间坐标系,
…………(2分)
∵PA=PD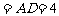 ,∴
,∴ ,
,
得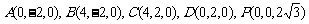 ,
,
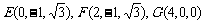 ,
,
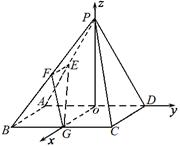 故
故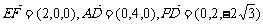 ,
,
∵ ,
,
∴EF 平面PAD;
…………(4分)
平面PAD;
…………(4分)
(II)解: ,
,
设平面EFG的一个法向量为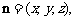
则 ,
, 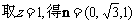 ,…………(7分)
,…………(7分)
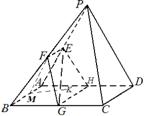 平面ABCD的一个法向量为
平面ABCD的一个法向量为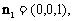 ……[以下同方法1]
……[以下同方法1]
方法3:(I)证明:∵平面PAD⊥平面ABCD,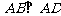 ,
,
∴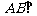 平面PAD,
…………(2分)
平面PAD,
…………(2分)
∵E、F为PA、PB的中点,
∴EF//AB,∴EF 平面PAD; …………(4分)
平面PAD; …………(4分)
(II)解:∵ EF//HG,AB//HG,∴HG是所二面角的棱,
…………(6分)
∵HG // EF,∴ 平面PAD, ∴DH
平面PAD, ∴DH HG,EH
HG,EH HG ,
HG ,
∴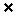 EHA是锐二面角的平面角,等于
EHA是锐二面角的平面角,等于 ;
………(8分)
;
………(8分)
(III)解:过M作MK⊥平面EFG于K,连结KF,
则 KFM即为MF与平面EFG所成角, ………(10分)
KFM即为MF与平面EFG所成角, ………(10分)
因为AB//EF,故AB/平面EFG,故AB/的点M到平面EFG的距离等于A到平面EFG的距离,∵ 平面PAD,∴平面EFGH
平面PAD,∴平面EFGH 平面PBD于EH,
平面PBD于EH,
∴A到平面EFG的距离即三角形EHA的高,等于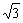 ,即MK
,即MK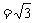 ,
,
∴ ,
, ,在直角梯形
,在直角梯形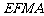 中,
中,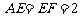 ,
,
∴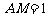 或
或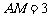 ∵M靠近A,∴
∵M靠近A,∴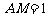 …………(11分)
…………(11分)
∴当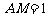 时, MF与平面EFG所成角正弦值等于
时, MF与平面EFG所成角正弦值等于 .…………(12分)
.…………(12分)
3. ⑴证明:因为 ,且
,且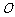 为
为 的中点,所以
的中点,所以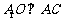 .
.
又由题意可知,平面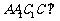 平面
平面 ,交线为
,交线为 ,且
,且 平面
平面 ,
,
所以 平面
平面 .
.
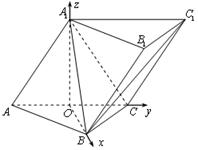
⑵如图,以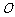 为原点,
为原点,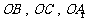 所在直线分别为
所在直线分别为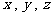 轴建立空间直角坐标系.
轴建立空间直角坐标系.
由题意可知,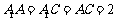 ,又
,又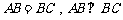
∴ .
.
所以得: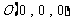 ,
,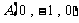 ,
, ,
, ,
,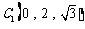 ,
,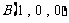 ,则有:
,则有:
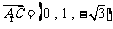 ,
,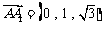 ,
,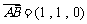 .
.
设平面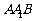 的一个法向量为
的一个法向量为 ,则有
,则有
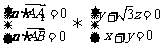 ,令
,令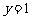 ,得
,得 ,
,
所以 .
.
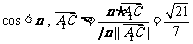 .
.
因为直线 与平面
与平面 所成角
所成角 和向量
和向量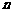 与
与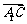 所成锐角互余,
所成锐角互余,
所以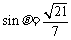 .
.
⑶设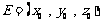 ,
,
即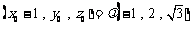 ,得
,得 .
.
所以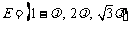 ,得
,得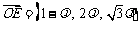
令 平面
平面 ,得
,得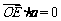 ,即
,即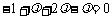 ,得
,得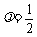 ,
,
即存在这样的点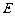 ,
,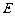 为
为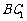 的中点.
的中点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com