
2. (Ⅰ)以D为原点,DA、DC、DD1分别为
x、y、z轴,建立如图所示的空间直角坐标系O-xyz.
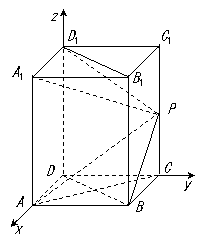 则D(0,0,0), A(1,0,0), B(1,1,0), C(0,1,0),
则D(0,0,0), A(1,0,0), B(1,1,0), C(0,1,0),
D1 (0,0,2),A1 (1,0,2),B1 (1,1,2),C1 (0,1,2), P(0,1,m),
所以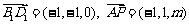 ,
,
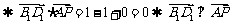 .………4分
.………4分
(Ⅱ)∵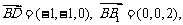
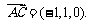
又∵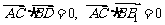 ,
,
∴ 的一个法向量.
的一个法向量.
设直线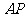 与平面
与平面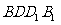 所成的角为
所成的角为 ,
,
则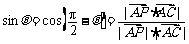
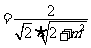 =
= ,解得
,解得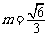 .
.
故当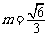 时,直线AP与平面
时,直线AP与平面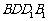 所成角为60º.………………8分
所成角为60º.………………8分
(Ⅲ)∵m=1,∴P(0,1,1),∴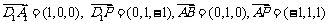 .
.
设平面PA1D1的法向量为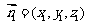 ,可求得
,可求得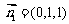 ,
,
设平面PAB的法向量为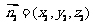 ,可求得
,可求得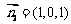 .
.
∴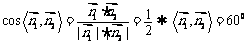 ,
,
故平面PA1D1与平面PAB所成角为600. ………………12分
1. 解法一:(1)∵BOCD为正方形,
∴BC⊥OD,折起后OD为AD在面BOCD上的射影,由三垂线定理知:BC⊥AD ……(3分)
(2)设BC交OD于E点,过E作EF⊥DA于F,连接CF,则CF⊥AD,
 则∠CFE为所求二面角的平面角。
则∠CFE为所求二面角的平面角。
显然CE=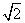 ,在RtΔAOD中,OA=2,OD=2
,在RtΔAOD中,OA=2,OD=2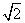 ,则AD=2
,则AD=2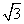 ,
,
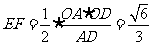 ,
,
∴tan∠CFE=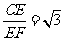 ,∴∠CFE=
,∴∠CFE=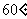 ………(8分)
………(8分)
(3)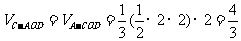 ……(12分)
……(12分)
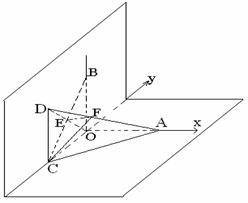
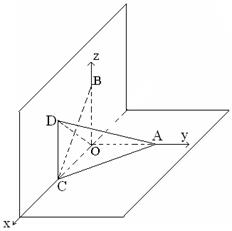
解法二:建立空间坐标系如图所示,
此时A(0,2,0),B(0,0,2),C(2,0,0),D(2,0,2)
(1)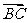 =(2,0,-2),
=(2,0,-2),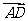 =(2,-2,2),∵
=(2,-2,2),∵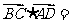 4-4=0,∴BC⊥AD……(3分)
4-4=0,∴BC⊥AD……(3分)
 (2)取平面OAD的法向量
(2)取平面OAD的法向量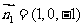 ,由于
,由于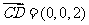 ,
,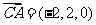 取平面CAD的法向量
取平面CAD的法向量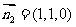
则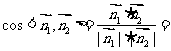
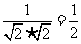 ,∴所求二面角为60° ………(8分)
,∴所求二面角为60° ………(8分)
(3)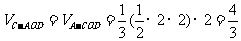
………………………(12分)
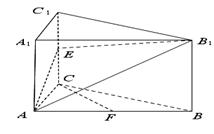
11.(2011北京朝阳区一模)
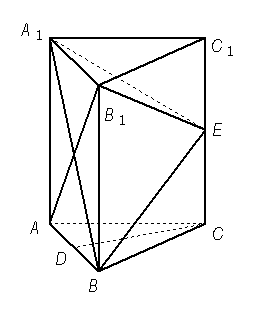
如图,在三棱柱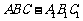 中,每个侧面均为正方形,
中,每个侧面均为正方形,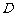 为底边
为底边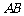 的中点,
的中点,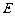 为侧棱
为侧棱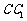 的中点.
的中点.
⑴求证: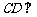 平面
平面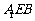 ;
;
 ⑵求证:
⑵求证: 平面
平面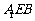 ;
;
⑶求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
2010年新课标省市高三数学模拟题分类
第四节 立体几何、空间向量详解答案
10.(2010浙江省考前预测卷)
如图,三棱锥P-ABC中,PC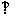 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD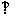 平面PAB.
平面PAB.
(1)求证:AB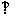 平面PCB;
平面PCB;
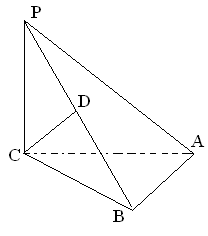 (2)求异面直线AP与BC所成角的大小;
(2)求异面直线AP与BC所成角的大小;
(3)求平面PAC和平面PAB所成锐二面角的余弦值.
9.(2010吉林农安中学高三冲刺卷)
如图1,直角梯形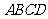 中,
中,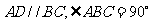 ,
,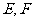 分别为边
分别为边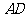 和
和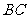 上的点,且
上的点,且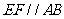 ,
,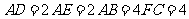 .将四边形
.将四边形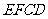 沿
沿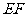 折起成如图2的位置,使
折起成如图2的位置,使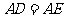 .
.
(Ⅰ)求证: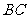
 平面
平面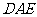 ;
;
(Ⅱ)求四棱锥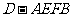 的体积;
的体积;
(Ⅲ)求面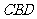 与面
与面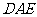 所成锐二面角的余弦值.
所成锐二面角的余弦值.

8.(2010福建泉州一中最后模拟)
右图为一简单组合体,其底面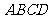 为正方形,
为正方形,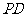
 平面
平面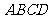 ,
,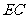 //
//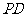 ,且
,且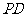 =
=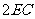 。
。
(1)求证: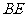 //平面
//平面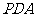 ;
;
(2)若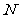 为线段
为线段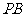 的中点,
的中点,
求证: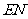
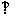 平面
平面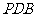 ;
;
(3)若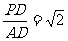 ,求平面
,求平面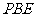 与平面
与平面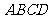 所成的二面角的大小。
所成的二面角的大小。
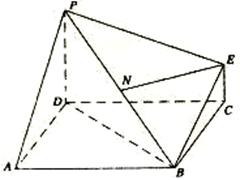
7.(2010北京丰台区一模)
如图,在底面是正方形的四棱锥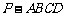 中,
中,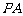
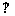 面
面 ,
,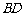 交
交 于点
于点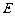 ,
,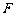 是
是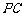 中点,
中点,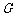 为
为 上一点.
上一点.
⑴求证: ;
;
⑵确定点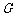 在线段
在线段 上的位置,使
上的位置,使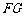 //平面
//平面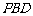 ,并说明理由.
,并说明理由.
⑶当二面角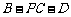 的大小为
的大小为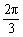 时,求
时,求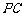 与底面
与底面 所成角的正切值.
所成角的正切值.
6.(2010东北师大附中最后一模)
 如图,在直三棱柱
如图,在直三棱柱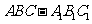 中,
中, ,
,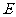 是棱
是棱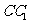 上的动点,
上的动点, 是
是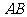 中点
,
中点
,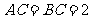 ,
,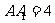 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若二面角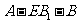 的大小是
的大小是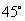 ,求
,求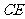 的长.
的长.
5.(2010吉林实验中学模拟)
如图,在底面为直角梯形的四棱锥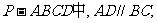
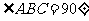
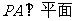
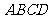 ,
,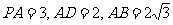 ,
,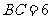
(Ⅰ)求证: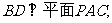
 (Ⅱ)求二面角
(Ⅱ)求二面角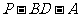 的大小.
的大小.
4.(2010辽宁丹东二模)
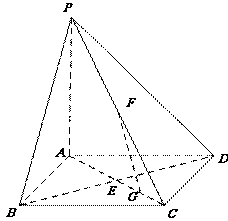
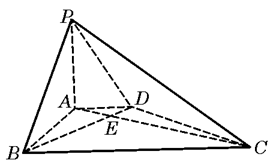
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
(I)求证:EF 平面PAD;
平面PAD;
(II)求平面EFG与平面ABCD所成锐二面角的大小;
(III)若M为线段AB上靠近A的一个动点,问当AM长度等于多少时,直线MF与平面EFG所成角的正弦值等于 ?
?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com