
18、(本题13分)已知f(x)=是奇函数,且f(2)=.
(1)求实数p,q的值;
(2)判断函数f(x)在(-∞,-1)上的单调性,并加以证明.
17、(本题13分)求由曲线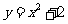 与
与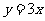 ,
,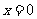 ,
,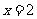 所围成的平面图形的面积。 (画出图形)。
所围成的平面图形的面积。 (画出图形)。
16、(本题13分) 已知命题P函数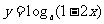 在定义域上单调递增;命题Q不等式
在定义域上单调递增;命题Q不等式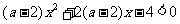 对任意实数
对任意实数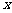 恒成立若
恒成立若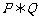 是真命题,求实数
是真命题,求实数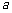 的取值范围。
的取值范围。
15、定义在 上的偶函数
上的偶函数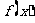 满足
满足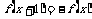 ,且在
,且在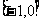 上是增函数,下面是关于f(x)的判断:
上是增函数,下面是关于f(x)的判断:
①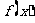 是周期函数;
②
是周期函数;
②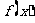 的图像关于直线
的图像关于直线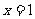 对称;
③
对称;
③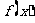 在[0,1]上是增函数; ④
在[0,1]上是增函数; ④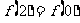 .其中正确的判断是_____________________(把你认为正确的判断都填上)
.其中正确的判断是_____________________(把你认为正确的判断都填上)
三、解答题:(共80分,解答应写出文字说明,证明过程或演算步骤)
14、若对任意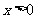 ,
,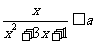 恒成立,则
恒成立,则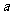 的取值范围是 __
的取值范围是 __
13、直线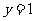 与曲线
与曲线 有四个交点,则
有四个交点,则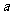 的取值范围是 .
的取值范围是 .
12、已知函数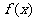 的导函数为
的导函数为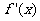 ,且满足
,且满足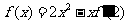 ,则
,则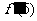 =
=
11、函数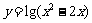 的定义域是____________________.
的定义域是____________________.
10、已知定义在R上的偶函数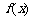 ,满足
,满足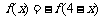 ,且当
,且当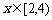 时,
时,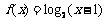 ,则
,则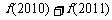 的值为
( )
的值为
( )
A、 B、
B、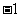 c、
c、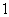 D、
D、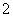
9、若函数f(x)=x- 在(1,+∞)上是增函数,则实数p的取值范围是 ( )
A、[-1,+∞) B、[1,+∞) C、(-∞,-1] D、(-∞,1]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com