
2、根据拼音写出相应的汉字。shòu(狩)猎,cuàn(篡)夺,rǎo(扰)乱,更胜一chóu(筹),gōu(篝)火,zhōng(螽)斯,xī(窸)sū(窣)作响,wō jù(莴)(苣)
1、给加粗的字注音。喧嚣(xiāo),劫掠(jié),静谧(mì),酷爱(kù) 吮取(shǔn),气氛(fēn) 满载而归(zài) 喑哑(yīn)(yǎ)
21.(14分)已知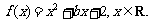
(1)若函数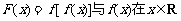 时有相同的值域,求b的取值范围;
时有相同的值域,求b的取值范围;
(2)若方程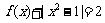 在(0,2)上有两个不同的根x1、x2,求b的取值范围,并证明
在(0,2)上有两个不同的根x1、x2,求b的取值范围,并证明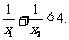
龙泉中学2011届理科高三数学综合练习(7)
20.(13分)定义在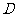 上的函数
上的函数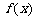 ,如果满足:对任意
,如果满足:对任意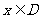 ,存在常数
,存在常数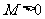 ,都有
,都有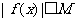 成立,则称
成立,则称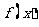 是
是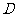 上的有界函数,其中
上的有界函数,其中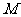 称为函数
称为函数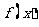 的上界.
的上界.
已知函数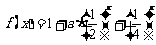 ;
;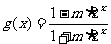 .
.
(1)当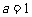 时,求函数
时,求函数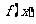 在
在 上的值域,并判断函数
上的值域,并判断函数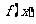 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数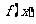 在
在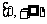 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数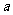 的取值范围;
的取值范围;
(3)若常数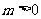 ,函数
,函数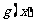 在
在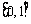 上的上界是
上的上界是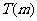 ,求
,求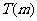 的取值范围.
的取值范围.
19.(12分)设函数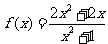 ,函数
,函数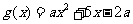 .
.
(1)求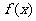 在
在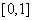 上的值域;
上的值域;
(2)若对于任意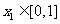 ,总存在
,总存在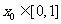 ,使得
,使得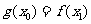 成立,求
成立,求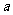 的取值范围.
的取值范围.
18.(12分) 设函数 .
.
(Ⅰ)求函数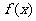 的单调区间;
的单调区间;
(Ⅱ)若函数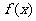 在
在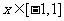 内没有极值点,求
内没有极值点,求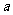 的取值范围;
的取值范围;
(Ⅲ)若对任意的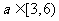 ,不等式
,不等式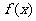 ≤
≤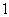 在
在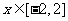 上恒成立,求
上恒成立,求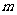 的取值范围.
的取值范围.
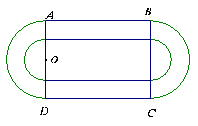
17.(12分)某学校要建造一个面积为10000平方米的运动场。如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成。跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮。已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元。设半圆的半径OA=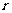 (米), (1)试建立塑胶跑道面积S与
(米), (1)试建立塑胶跑道面积S与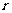 的函数关系S(
的函数关系S(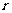 )
)
(2)由于条件限制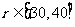 ,问当
,问当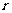 取何值时,运动场造价最低?(精确到元)
取何值时,运动场造价最低?(精确到元)
16.(12分)已知函数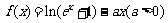 .
.
(1)若函数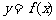 的导函数是奇函数,求
的导函数是奇函数,求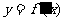 的值域;
的值域;
(2)求函数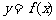 的单调区间.
的单调区间.
15.设集合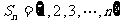 ,若
,若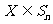 ,把
,把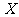 的所有元素的乘积称为
的所有元素的乘积称为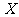 的容量(若
的容量(若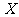 中只有一个元素,则该元素的数值即为它的容量,规定空集的容量为0).若
中只有一个元素,则该元素的数值即为它的容量,规定空集的容量为0).若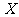 的容量为奇(偶)数,则称
的容量为奇(偶)数,则称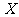 为
为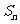 的奇(偶)子集.若
的奇(偶)子集.若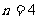 ,则
,则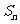 的所有偶子集的容量之和为_______.
的所有偶子集的容量之和为_______.
14.已知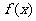 是定义在R上的函数,存在反函数,且
是定义在R上的函数,存在反函数,且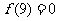 ,若
,若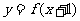 的反函数是
的反函数是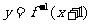 ,则
,则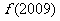 = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com