
14.解⑴曲线C的直角坐标方程是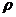 =4cos
=4cos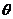 ,化为直角坐标方程为:
,化为直角坐标方程为:
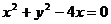 …………2分
…………2分
直线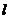 的直角坐标方程为:
的直角坐标方程为: …………2分
…………2分
⑵(法一)由⑴知:圆心的为(2,0),圆的半径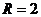 ,
,
圆心到直线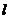 的距离
的距离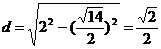 ,…………6分
,…………6分
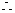
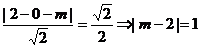 …………8分
…………8分
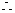
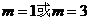 …………10分
…………10分
(法二)
把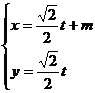 (
(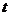 是参数)代入方程
是参数)代入方程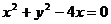
得 …………6分
…………6分
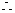
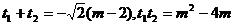
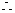 |AB|=
|AB|=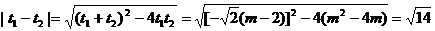 …8分
…8分
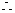
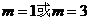 …………10分
…………10分
13. 解⑴在 和
和 中,
中,
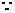 AB=AC
AB=AC  ABE=
ABE= ACD ……2分
ACD ……2分
又 BAE=
BAE= EDC
EDC
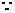 BD//MN
BD//MN
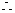
 EDC=
EDC= DCN
DCN
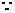 直线是圆的切线
直线是圆的切线
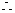
 DCN=
DCN= CAD
CAD
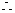
 BAE=
BAE= CAD
CAD
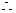
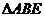
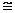
 (SAS) ……5分
(SAS) ……5分
⑵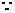
 EBC=
EBC= BCM
BCM
 BCM=
BCM= BDC
BDC
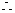
 EBC=
EBC= BDC=
BDC= BAC BC=CD=4
BAC BC=CD=4
又 BEC=
BEC= BAC+
BAC+ ABE=
ABE= EBC+
EBC+ ABE=
ABE= ABC=
ABC= ACB
ACB
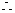 BC=BE=4……8分
BC=BE=4……8分
设AE=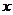 。易证
。易证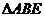 ∽
∽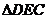
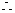
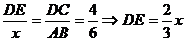
又AE·EC=BE·ED EC=6-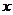
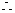 4·
4·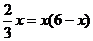
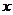 =
=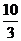 …………10分
…………10分
12.解:(I)原不等式可化为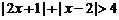
当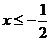 时,不等式化为
时,不等式化为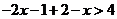 ,∴
,∴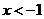 ,此时
,此时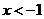 ;
;
当 时,不等式化为
时,不等式化为 ,∴
,∴ ,此时
,此时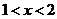 ;
;
当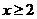 时,不等式化为
时,不等式化为 ,∴
,∴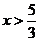 ,此时
,此时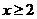 .
.
综上可得:原不等式的解集为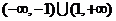 .
……………(5分)
.
……………(5分)
(II)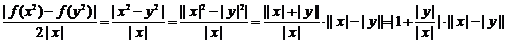
……………(8分)
∵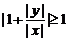 ,当
,当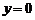 时取等号,∴
时取等号,∴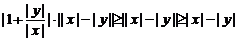
因此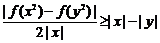 ……………(10分)
……………(10分)
11.解:(I)直线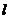 的参数方程为
的参数方程为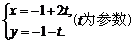 ,
……………(2分)
,
……………(2分)
(或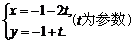 ;或
;或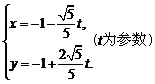 .等形式均可
.等形式均可
曲线 的参数方程是
的参数方程是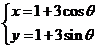 (θ为参数) ……………(5分)
(θ为参数) ……………(5分)
(II)直线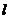 的普通方程为
的普通方程为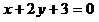 ,
,
曲线 普通方程为
普通方程为 ,
……………(7分)
,
……………(7分)
联立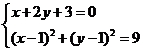 ,
,
解得交点的直角坐标为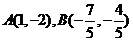 ……………(10分)
……………(10分)
10. 证明:(I)连结PB.∵BC切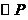 于点B,∴PB⊥BC.
于点B,∴PB⊥BC.
又∵EF⊥CE,且∠PCB=∠FCE,∴Rt△CBP∽Rt△CEF,
∴∠CPB=∠CFE,∴∠EPB+∠EFB=180°,∴四点B,P,E,F共圆……………(5分)
(II)∵四点B,P,E,F共圆,且EF⊥CE, PB⊥BC,∴此圆的直径就是PF.
∵BC切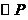 于点B,且
于点B,且 ,
,
∴由切割线定理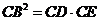 ,得:CE=4,DE=2,BP=1.
,得:CE=4,DE=2,BP=1.
又∵Rt△CBP∽Rt△CEF,∴EF:PB=CE:CB,
得 .
.
在Rt△FEP中,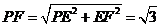 ,
,
即由四点B,P,E,F确定圆的直径为 ……………(10分)
……………(10分)
9.证明:(I)∵ ,∴
,∴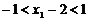 ,即
,即 ,
…………(2分)
,
…………(2分)
同理 ,∴
,∴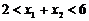 ,
…………(4分)
,
…………(4分)
∵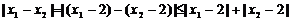 ,
,
∴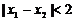 ;
…………(5分)
;
…………(5分)
(II)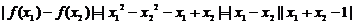 ,…………(8分)
,…………(8分)
∵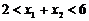 ,∴
,∴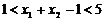 ,
,
8.解:(I)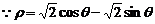 ,
,
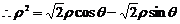 ,
…………(2分)
,
…………(2分)
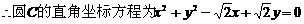 ,
…………(3分)
,
…………(3分)
即 ,
,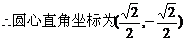 .…………(5分)
.…………(5分)
(II)方法1:直线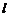 上的点向圆C 引切线长是
上的点向圆C 引切线长是
 ,
,
…………(8分)
∴直线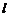 上的点向圆C引的切线长的最小值是
上的点向圆C引的切线长的最小值是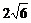 …………(10分)
…………(10分)
方法2: ,
…………(8分)
,
…………(8分)
圆心C到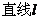 距离是
距离是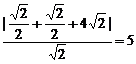 ,
,
∴直线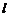 上的点向圆C引的切线长的最小值是
上的点向圆C引的切线长的最小值是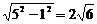 …………(10分)
…………(10分)
7. 解:(I)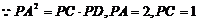 ,
,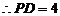 , …………(2分)
, …………(2分)
又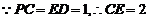 ,
,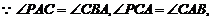
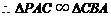 ,
, ,
…………(4分)
,
…………(4分)
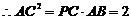 ,
, …………(5分)
…………(5分)
(II)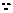
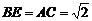 ,
,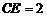 ,而
,而 , …………(8分)
, …………(8分)
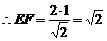 ,
, .
…………(10分)
.
…………(10分)
6.(1)当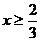 时,
时,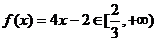 …………2
…………2
当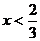 时,
时, ,………4
,………4
所以,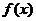 的值域为
的值域为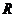 ;………5
;………5
(2)当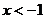 时,原不等式
时,原不等式 ,
,
此时解集为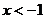 ;……6
;……6
当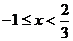 时,原不等式
时,原不等式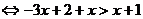 ,
,
此时解集为 ;……7
;……7
当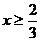 时,原不等式
时,原不等式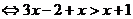 ,
,
此时解集为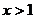 ;………8
;………8
综上,不等式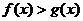 的解集为
的解集为 ………………10
………………10
5.(1) ;………4
;………4
(2)设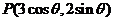 ,
,
则 =
=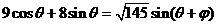 ……6
……6
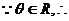 当
当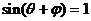 时,
时, 的最大值为
的最大值为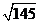 …………10
…………10
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com