
3、化简方程: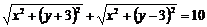
2、求适合下列条件的椭圆的标准方程:
(1)两个焦点坐标分别是(-4,0),(4,0)椭圆上一点P到两焦点的距离的和等于10;
(2)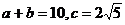
(3)与椭圆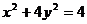 有公共焦点,且经过点
有公共焦点,且经过点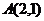
1、判定下列椭圆的焦点在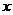 轴上还是在
轴上还是在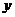 轴上,写出焦点坐标及焦距
轴上,写出焦点坐标及焦距
(1)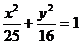 (2)
(2)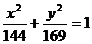
引入:曲线与方程同时具有纯粹性和完备性,通俗将是动点按照某种规律运动形成的轨迹叫曲线。问:(1)在画图的过程中,绳子长度变化了吗?(2)动点与两个定点有什么关系,如何表述椭圆的定义?
(一)新授:
1、椭圆的定义:平面内与两定点的距离等于常数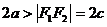 的点的轨迹。两定点称为焦点,
的点的轨迹。两定点称为焦点,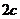 为焦距。注意:
①
为焦距。注意:
①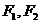 为两个定点
②
为两个定点
② 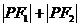 为常数 ③
为常数 ③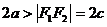 才是椭圆
④如果
才是椭圆
④如果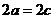 则
则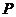 点的轨迹是线段
点的轨迹是线段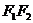 ⑤如果
⑤如果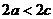 则点
则点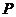 的轨迹不存在
2、求椭圆的标准方程
解:以
的轨迹不存在
2、求椭圆的标准方程
解:以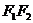 所在直线为
所在直线为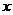 轴,线段
轴,线段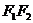 的中垂线为
的中垂线为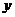 轴,建立平面直角坐标系。
(如图2-14).设
轴,建立平面直角坐标系。
(如图2-14).设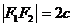 ,
,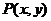 为椭圆上任意一点,则有
为椭圆上任意一点,则有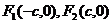 .
.
由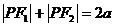 得方程为
得方程为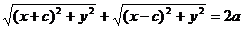
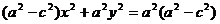 整理得:
整理得: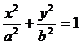
焦点在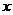 轴上
轴上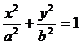 (
(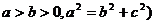
焦点在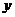 轴上
轴上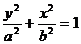 (
(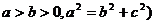 分母谁大焦点就在哪个轴上,只要两个条件就能得方程,且
分母谁大焦点就在哪个轴上,只要两个条件就能得方程,且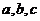 在图中能找到相应的线段
在图中能找到相应的线段
焦点位置不知在哪个轴上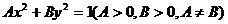
3、方法:①定义法②待定系数法 (二)例题讲解
3、帮助学生树立运动变化的观点,培养学生的探索能力和进取精神
2、学会用待定系数法与定义求椭圆的方程
1、能正确运用椭圆的定义与标准方程解题
椭圆及标准方程(第一课时)
(二)实例
例1:《名师》P32例1
例2:方程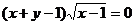 所表示的曲线
所表示的曲线
例3求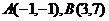 的中垂线的方程(课本P35例2)
的中垂线的方程(课本P35例2)
例4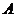 为定点,线段
为定点,线段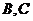 在定直线
在定直线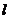 上滑动,已知
上滑动,已知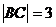 ,求
,求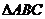 的外心的轨迹方程(《名师》P33变式2)
的外心的轨迹方程(《名师》P33变式2)
例5过点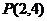 作两条互相垂直的直线交
作两条互相垂直的直线交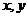 轴于
轴于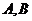 两点,设
两点,设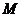 为线段
为线段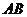 的中点,求点
的中点,求点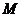 的轨迹方程。(直接法)
的轨迹方程。(直接法)
例6点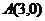 为单位圆外一点,
为单位圆外一点,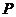 为圆上任意一点,若
为圆上任意一点,若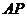 的中点为
的中点为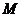 ,当
,当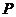 在圆上运动时,求点
在圆上运动时,求点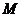 的轨迹方程。(代入法、定义法)
的轨迹方程。(代入法、定义法)
(一)新授
1、研究方程的曲线
2、如何求曲线的方程,三种方法:定义法,直接法,代入法。
3、直接法求点的轨迹步骤:建系设点→满足条件→列出方程→化简→证明,通常第三和五部可省略,但要注意有无遗漏增生一些点,常见的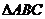 中三点不共线,直线点斜式要满足斜率存在等。
中三点不共线,直线点斜式要满足斜率存在等。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com