22．(2006全国Ⅱ)(12分)已知抛物线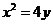的焦点为F, A, B是抛物线上的两动点，且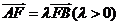．过A、B两点分别作抛物线的切线，设其交点为M。

(I)证明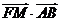为定值；

(II)设的面积为S，写出S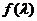＝的表达式，并求S的最小值。

综合检测题答案

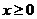21．(2006全国Ⅱ)设函数，若对所有的，都有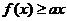成立，求实数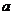的取值范围．

20．(12分)已知数列{a_n}满足(n－1)a_n+1=(n+1)(a_n－1)且a₂=6,设b_n=a_n+n(n∈N*)．

(1)求{b_n}的通项公式；

(2)求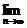(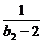++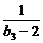+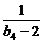…+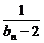)的值．

19．(12分)如图，将长AA′=3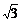，宽AA₁=3的矩形沿长的三等分线处折叠成一个三棱柱，如图所示：

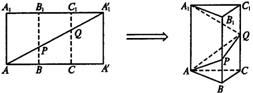
　 (1)求平面APQ与底面ABC所成二面角的正切值；

　 (2)求三棱锥A₁-APQ的体积．

18．(12分,2005北京)甲、乙两人各进行3次射击，甲每次击中目标的概率为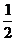，乙每次击中目标的概率，

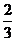　 (I)记甲击中目标的次数为ξ，求ξ的概率分布及数学期望Eξ；

　 (II)求乙至多击中目标2次的概率；

　 (III)求甲恰好比乙多击中目标2次的概率．

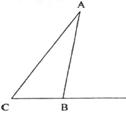
17．(10分)如图ΔABC中，角A、B、C的对边长分别为a、b、c，∠C=60°，a＝1，且b=c+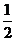．求AC的长度的最小值，及此时BC的长度。

16．下列四个命题：

　 ①分别和两条异面直线相交的两条直线一定是异面直线；

　 ②一个平面内任意一点到另一个平面之距离均相等，那么这两个平面平行；

③一个二面角的两个半平面分别垂直于另一个二面角的两个半平面，则这两个二面角的平面角相等或互补；

　 ④过两异面直线外一点能作且只能作出一条直线和这两条异面直线同时相交．

　 其中正确命题的序号是____________．

15．(ax+1)⁵(x+1)²展开式中x²的系数为21，则a=___________．

14．三个人坐在一排八个座位上，若每人的两边都要有空位，则不同的坐法种数为__________．

解析：根据题意，两端的座位要空着，中间6个座位坐三个人，再空三个座位，这三个座位之间产生四个空，可以认为是坐后产生的空．故共有种．这种执果索因的思考方法是处理排列、组合问题常用的方法．

答案：24

13．设函数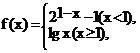若f(x₀)＞1，则x₀的取值范围是__________