
1.(本小题满分12分)
已知向量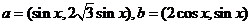 ,定义
,定义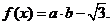
(I)求函数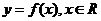 的单调递减区间;
的单调递减区间;
(II)若函数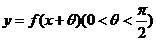 为偶函数,求
为偶函数,求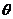 的值。
的值。
6.(本题满分12分)
解: 4. (Ⅰ)∵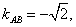
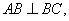 1分
1分
∴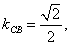 ∴
∴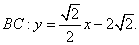 5分
5分
(Ⅱ)在上式中,令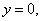 得:
得: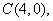 6分
6分
∴圆心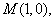 . 7分
. 7分
又∵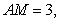 .8分
.8分
∴外接圆的方程为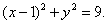 9分
9分
(Ⅲ)∵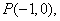
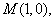
∵圆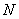 过点
过点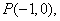 ,∴
,∴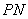 是该圆的半径,
是该圆的半径,
又∵动圆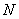 与圆
与圆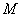 内切,∴
内切,∴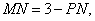
即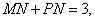 .11分
.11分
∴点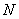 轨迹是以
轨迹是以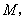
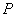 为焦点,长轴长为3椭圆.
为焦点,长轴长为3椭圆.
∴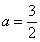 ,
, 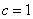 ,
,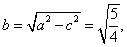 .
.
∴轨迹方程为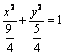 . 14分
. 14分
5.(本题满分14分)
(I)
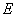 为线段
为线段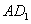 的中点,
的中点,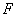 为线段
为线段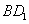 的中点,
的中点,
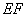 ∥
∥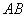 ,
,

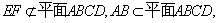

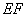 ∥面
∥面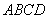 .
.
(II)当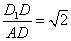 时,
时,
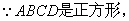
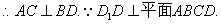
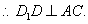
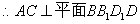
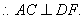
 ∴
∴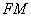 ∥
∥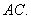
∴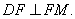 ∵
∵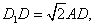 ∴
∴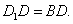
∴矩形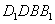 为正方形,∵
为正方形,∵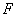 为
为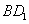 的中点,
的中点,
∴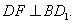 ∵
∵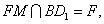
∴
20、解:(1)当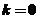 时,
时,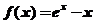 ,
,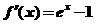
∴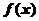 在
在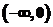 上单调减,在
上单调减,在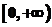 上单调增.
上单调增.
∴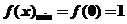 ,
………5分
,
………5分
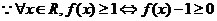 成立,
成立,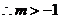 ………7分
………7分
(2)当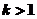 时,
时,
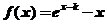 ,
,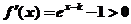 在
在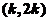 上恒成立. …9分
上恒成立. …9分
∴ 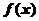 在
在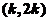 上单调增.(且连续)
上单调增.(且连续)
且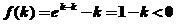 ,…………10分
,…………10分
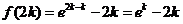

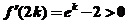 ,
,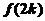 在
在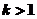 时单调增,∴
时单调增,∴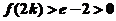 ………13分
………13分
∴由零点存在定理知,函数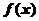 在
在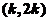 内存在零点.
…………14分
内存在零点.
…………14分
4.(本题满分14分)
19.解:(1) …………1分
…………1分
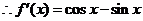 ,
…………2分
,
…………2分
∴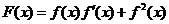
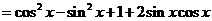
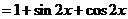
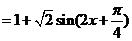 ………5分
………5分
∴当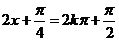
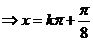 (
(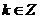 )时,
)时,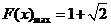
最小正周期为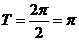 ………7分
………7分
(2)∵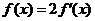
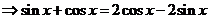
∴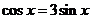
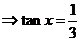 …………10分
…………10分
∴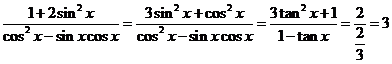 ……14分
……14分
3.(本题满分14分)
2.(本题满分12分)
解(Ⅰ)由已知可得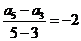 ,则公差
,则公差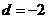 , …………………2分
, …………………2分
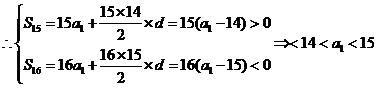 …………………7分
…………………7分
(Ⅱ)最大的值是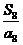 …………………8分
…………………8分
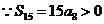
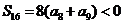 …………………10分
…………………10分
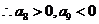 即
即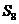 最大
…………………11分
最大
…………………11分
又当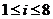 时,
时, ;当
;当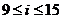 时,
时,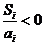 ,数列
,数列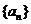 递减…………………13分
递减…………………13分
所以, 最大…………………14分
最大…………………14分
16.解: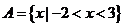 ,
,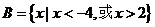 ,
,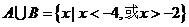 ,
,
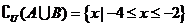 ,而
,而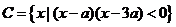 .…………7分
.…………7分
(1) 当a>0时,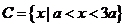 ,显然不成立
…………9分
,显然不成立
…………9分
(2) 当a=0时,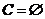 ,不成立
…………10分
,不成立
…………10分
(3) 当a<0时,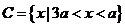 ,要使
,要使 ,只需
,只需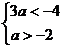 ,即
,即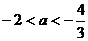 …………12分
…………12分
1.(本题满分12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com