
16.解:(I)因为 ,所以
,所以 ,由
,由 ,即
,即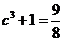 ,
, .
.
又因为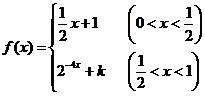 在
在 处连续,
处连续,
所以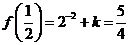 ,即
,即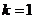 .
.
(Ⅱ)由(1)得:
由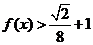 得,当
得,当 时,解得
时,解得 .
.
当 时,解得
时,解得 ,
,
所以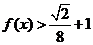 的解集为
的解集为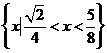 .
.
11.  12. -2 13 .2 14 . -1 15. r+1,
12. -2 13 .2 14 . -1 15. r+1, 
1. D 2. C 3.D 4. A 5.B 6.B 7.C 8. C 9. A 10.A
21.(本题满分14分)
已知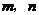 为正整数
为正整数
(Ⅰ)用数学归纳法证明:当 时,
时,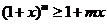 ;
;
(Ⅱ)对于 ,已知
,已知 ,求证:
,求证: ,
, ;
;
(Ⅲ)求出满足等式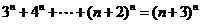 的所有正整数
的所有正整数 .
.
麻城博达学校2010届高三阶段测试(二)
理科数学试题(B卷)
20.(本题满分13分)
首项为正数的数列{ }满足
}满足 .
.
(Ⅰ)证明:若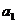 为奇数,则对一切
为奇数,则对一切 ,
, 都是奇数;
都是奇数;
(Ⅱ)若对一切 ,都有
,都有 ,求
,求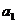 的取值范围.
的取值范围.
19.(本题满分12分)
设 是
是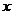 的三次多项式,已知
的三次多项式,已知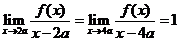 ,求
,求 的值(
的值( 为非零常数).
为非零常数).
17.(本题满分12分)
已知 ,
, 为常数.
为常数.
(Ⅰ)确定a与b的值;
(Ⅱ)求 的值.
的值.
18 (本题满分12分)
(本题满分12分)
一弹性小球自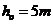 高处自由下落,当它与水平地面每碰撞一次后速度减少到碰前的
高处自由下落,当它与水平地面每碰撞一次后速度减少到碰前的 ,不计每次碰撞时间,则小球从开始下落到停止运动所经过的路程和时间分别是多少?(重力加速度取:
,不计每次碰撞时间,则小球从开始下落到停止运动所经过的路程和时间分别是多少?(重力加速度取:
 )
)
16.(本题满分12分)
已知函数 在区间
在区间 内连续,且
内连续,且 .
.
(Ⅰ)求实数 和
和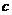 的值;
的值;
(Ⅱ)解不等式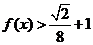 .
.
15. 将杨辉三角中的每一个数
将杨辉三角中的每一个数 都换成
都换成 ,就得到一个如下图所示的分数三角形,成为莱布尼茨三角形。从莱布尼茨三角形可看出
,就得到一个如下图所示的分数三角形,成为莱布尼茨三角形。从莱布尼茨三角形可看出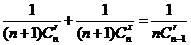 ,其中
,其中 .
.
令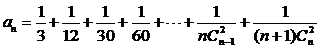 ,
,
则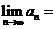 .
.
14.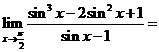 _____________.
_____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com