
62、(湖北省随州市2008年高三五月模拟)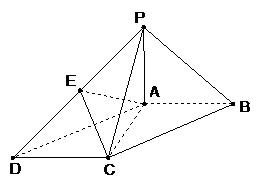 如图,在底面为平行四边形的四棱锥
如图,在底面为平行四边形的四棱锥 中,
中,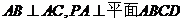 ,且
,且 ,点
,点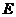 是
是 的中点。
的中点。
⑴求证: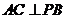 ;
;
⑵求证: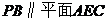 ;
;
⑶求二面角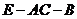 的大小。
的大小。

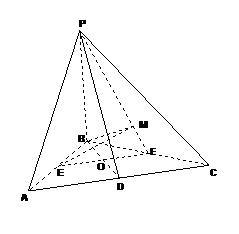
61、(湖北省荆州市2008届高中毕业班质量检测) 如图:在三棱锥
如图:在三棱锥 中,
中,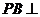 面
面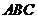 ,
,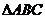 是直角三角形,
是直角三角形, ,
, ,
, ,点
,点 分别为
分别为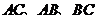 的中点。
的中点。
⑴求证: ;
;
⑵求直线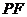 与平面
与平面 所成的角的大小;
所成的角的大小;
⑶求二面角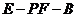 的正切值。
的正切值。
解:⑴连结 。在
。在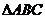 中,
中,

 ,点
,点 为
为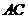 的中点,
的中点,

又
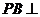 面
面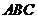 ,即
,即 为
为 在平面
在平面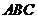 内的射影
内的射影



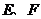 分别为
分别为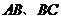 的中点
的中点
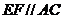


⑵
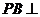 面
面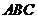 ,
,

连结 交
交 于点
于点 ,
,
 ,
,

 平面
平面

 为直线
为直线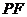 与平面
与平面 所成的角,且
所成的角,且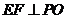

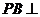 面
面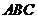 ,
,
 ,又
,又


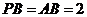 ,
,
 ,
,


 在
在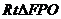 中,
中, ,
,

⑶过点 作
作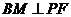 于点
于点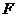 ,连结
,连结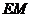 ,
,
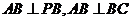 ,
,

 面
面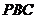 ,即
,即 为
为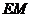 在平面
在平面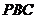 内的射影
内的射影

 ,
,
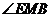 为二面角
为二面角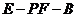 的平面角
的平面角

 中,
中, ,
,

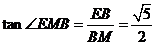
(其他解法根据具体情况酌情评分)
60、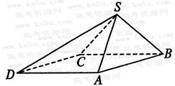 (湖北省黄冈中学2008届高三第一次模拟考试)四棱锥S-ABCD中,底面ABCD为平行四边形,侧面
(湖北省黄冈中学2008届高三第一次模拟考试)四棱锥S-ABCD中,底面ABCD为平行四边形,侧面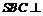 底面ABCD. 已知
底面ABCD. 已知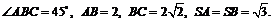
(1)证明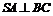 ;
;
(2)求直线SD与平面SAB所成角的大小.
 解法一:(1)作
解法一:(1)作 ,垂足为O,连结AO,由侧面
,垂足为O,连结AO,由侧面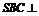 底面ABCD,得
底面ABCD,得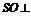 底面ABCD. 因为SA=SB,所以AO=BO. 又
底面ABCD. 因为SA=SB,所以AO=BO. 又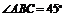 ,故
,故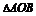 为等腰直角三角形,
为等腰直角三角形,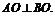 由三垂线定理,得
由三垂线定理,得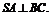
(2)由(1)知 ,依题设
,依题设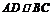 ,故
,故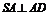 ,由
,由 ,得
,得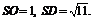 所以
所以 的面积
的面积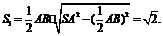 连结DB,得
连结DB,得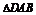 的面积
的面积 设D到平面SAB的距离为h,由
设D到平面SAB的距离为h,由 ,
,
得 ,解得
,解得
 设SD与平面SAB所成角为
设SD与平面SAB所成角为 ,则
,则 所以直线SD与平面SAB所成的角为
所以直线SD与平面SAB所成的角为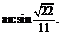
解法二:(1)作 ,垂足为O,连结AO,由侧面
,垂足为O,连结AO,由侧面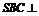 底面ABCD,得
底面ABCD,得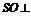 平面ABCD. 因为SA=SB,所以AO=BO. 又
平面ABCD. 因为SA=SB,所以AO=BO. 又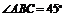 ,
,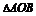 为等腰直角三角形,
为等腰直角三角形,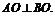
如图,以O为坐标原点,OA为x轴正向,建立直角坐标系O-xyz,
 ,所以
,所以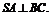
(2)取AB中点E, . 连结SE,取SE中点G,连结OG,
. 连结SE,取SE中点G,连结OG,
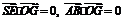 ,OG与平面SAB内两条相交直线SE、AB垂直,所以
,OG与平面SAB内两条相交直线SE、AB垂直,所以 平面SAB.
平面SAB. 的夹角记为
的夹角记为 ,SD与平面SAB所成的角记为
,SD与平面SAB所成的角记为 ,则
,则 与
与 互余.
互余.

所以直线SD与平面SAB所成的角为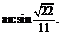
59、 (湖北省黄冈市麻城博达学校2008届三月综合测试)在四棱锥P-ABCD中,底面ABCD是a的正方形,
(湖北省黄冈市麻城博达学校2008届三月综合测试)在四棱锥P-ABCD中,底面ABCD是a的正方形,
PA⊥平面ABCD,且PA=2AB
(Ⅰ)求证:平面PAC⊥平面PBD;
(Ⅱ)求二面角B-PC-D的余弦值.
解:(Ⅰ)证明:∵PA⊥平面ABCD ∴PA⊥BD
∵ABCD为正方形 ∴AC⊥BD
∴BD⊥平面PAC又BD在平面BPD内,
∴平面PAC⊥平面BPD 6分
(Ⅱ)解法一:在平面BCP内作BN⊥PC垂足为N,连DN,
∵Rt△PBC≌Rt△PDC,由BN⊥PC得DN⊥PC;
∴∠BND为二面角B-PC-D的平面角,
 在△BND中,BN=DN=
在△BND中,BN=DN= ,BD=
,BD=
∴cos∠BND =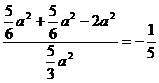
解法二:以A为原点,AB、AD、AP所在直线分别为x轴、y轴、z轴建立空间坐标系如图,在平面BCP内作BN⊥PC垂足为N连DN,
∵Rt△PBC≌Rt△PDC,由BN⊥PC得DN⊥PC;
∴∠BND为二面角B-PC-D的平面角
设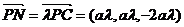

 10分
10分
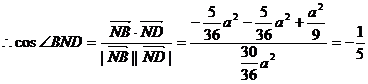 12分
12分
解法三:以A为原点,AB、AD、AP所在直线分别为x轴、y轴、z轴建立如图空间坐标系,作AM⊥PB于M、AN⊥PD于N,易证AM⊥平面PBC,AN⊥平面PDC,
 设
设


∵二面角B-PC-D的平面角与∠MAN互补
∴二面角B-PC-D的余弦值为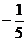 12分
12分
58、(湖北省鄂州市2008年高考模拟)(湖北省鄂州市2008年高考模拟)在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足
 (如图1).将△AEF沿EF折起到
(如图1).将△AEF沿EF折起到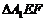 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小;
(Ⅲ)求二面角B-A1P-F的大小(用反三角函数表示).

解:不妨设正三角形 的边长为3,则
的边长为3,则
(1)在图1中,取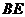 中点
中点 ,连结
,连结 ,
,
 则∵
则∵ 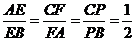 ,
,
∴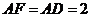 而
而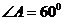 ,即△
,即△
 是正三角形
是正三角形
又∵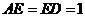 , ∴
, ∴
∴在图2中有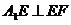 ,
, ,
,
∴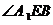 为二面角
为二面角 的平面角
的平面角
∵二面角 为直二面角, ∴
为直二面角, ∴
又∵ , ∴
, ∴ ⊥平面
⊥平面 ,即
,即 ⊥平面
⊥平面 .
.
(2)由(1)问可知A1E⊥平面BEP,BE⊥EF,建立如图的坐标系,则E(0,0,0),A1(0,0,1)B(2,0,0),F(0,0,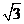 ).在图1中,不难得到EF//DP且EF=DP;DE// FP且DE=FP
).在图1中,不难得到EF//DP且EF=DP;DE// FP且DE=FP
故点P的坐标P(1,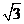 ,0)
,0)
∴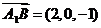 ,
, ,
,
不妨设平面A1BP的法向量 ,则
,则
令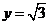 得
得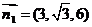 ∴
∴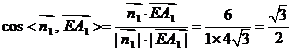
故直线A1E与平面A1BP所成角的大小为 .
.
(3)由(2)问可知平面A1BP的法向量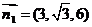 ,
, ,
,
设平面AEP的法向量 ,则
,则
令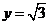 得
得 故
故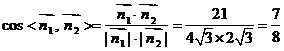
显然二面角B-A1P-F为钝角 故二面角B-A1P-F为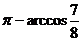 .
.
[方法探究]本题属于翻折问题,在翻折前的图1中易证EF⊥AB,而翻折后保持这一垂直关系,并且易证 ,从而有“三条直线两两垂直”,所以本例可以建立坐标系,利用空间向量求解.
,从而有“三条直线两两垂直”,所以本例可以建立坐标系,利用空间向量求解.
[技巧点拨]本题属于翻折问题,这是高考的热点题型. 求解翻折问题的策略是对比翻折前后,分析变与不变,一般地有:(1)分析翻折前后点的变化,注意点与点的重合问题以及点的位置的改变;(2)分析翻折前后长度与角度的变化,注意利用平面图形解决空间的线段长度以及空间角的大小;(3)若翻折后,线与线仍同在一个平面内,则它们的位置关系不发生任何变化;若翻折后,线与线由同一平面转为不同平面,则应特别注意点的位置变化.
57、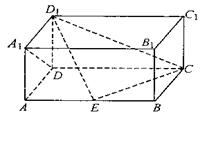 (湖北省三校联合体高2008届2月测试)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(湖北省三校联合体高2008届2月测试)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点A到面ECD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为 .
.
(1)证明:连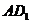 ,在长方体ABCD-A1B1C1D1中,
,在长方体ABCD-A1B1C1D1中,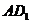 为
为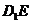 在平面
在平面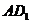 的射影,
的射影,
而AD=AA1=1,则四边形 是正方形
是正方形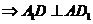 ,
,
由三垂线定理得D1E⊥A1D ……………3分
(2)解:以点D为原点,DA为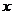 轴,DC为
轴,DC为 轴建立如图所示的直角坐标系。则
轴建立如图所示的直角坐标系。则
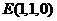 、
、 、
、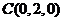 、
、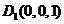 则
则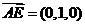 ,
,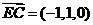 ,
,
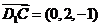 ,设平面
,设平面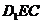 的法向量为
的法向量为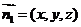

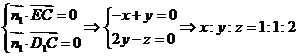 ,记
,记
 点A到面ECD1的距离
点A到面ECD1的距离 ……………7分
……………7分
(3)解:设 则
则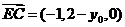 ,设平面
,设平面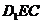 的法向量为
的法向量为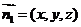

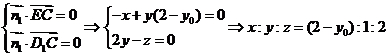 ,记
,记
而平面ECD的法向量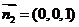 ,则二面角D1-EC-D的平面角
,则二面角D1-EC-D的平面角

 。
。
 当AE=
当AE=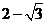 时,二面角D1-EC-D的大小为
时,二面角D1-EC-D的大小为 。……………12分
。……………12分
56、(湖北省八校高2008第二次联考) 如图,已知四棱锥
如图,已知四棱锥 中,
中, 是边长为
是边长为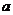 的正三角形,平面
的正三角形,平面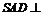 平面
平面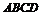 ,四边形
,四边形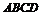 为菱形,
为菱形,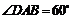 ,
, 为
为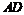 的中点,
的中点, 为
为 的中点.
的中点.
(Ⅰ)求证: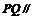 平面
平面 ;
;
(Ⅱ)求二面角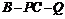 的大小.
的大小.
解:(1)证明取SC的中点R,连QR, DR.
由题意知:PD∥BC且PD=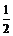 BC;
BC;
QR∥BC且QP=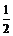 BC,
BC,
 QR∥PD且QR=PD.
QR∥PD且QR=PD.
 PQ∥DR, 又PQ
PQ∥DR, 又PQ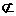 面SCD,
面SCD,
 PQ∥面SCD. …………(6分)
PQ∥面SCD. …………(6分)
(2)法一:连接SP,
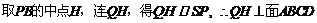 .
.
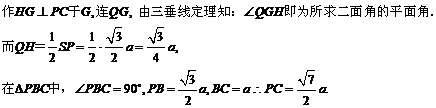
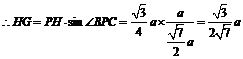 .
.  ,
,
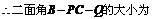
 …………(12分)
…………(12分)
(2)法二:以P为坐标原点,PA为x轴,PB为y轴,PS为z轴建立空间直角坐标系,
则S(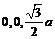 ),B(
),B(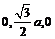 ),C(
),C( ),Q(
),Q(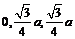 ).
).
面PBC的法向量为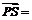 (
(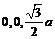 ),设
),设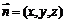 为面PQC的一个法向量,
为面PQC的一个法向量,
由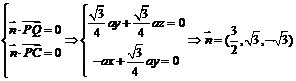 ,
,
cos ,
,
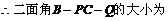
 …………(12分)
…………(12分)
55、(黑龙江省哈师大附中2008届高三上期末)如图,正方形ABCD中,AC∩BD=O,PO⊥平面ABCD,PO=AD=,点E在PD上,PE:ED=2:1。
(1)证明:PD⊥平面EAC;
 (2)求二面角A-PD-C的余弦值;
(2)求二面角A-PD-C的余弦值;
(3)求点B到平面PDC的距离。
解:(1)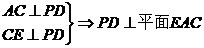
(2)∠CEA为二面角A-PD-C的平面角,
(3)点B到平面PDC的距离为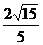
54、(黑龙江省哈尔滨九中2008年第三次模拟考试)已知斜三棱柱 的各棱长均为2, 侧棱
的各棱长均为2, 侧棱 与底面
与底面 所成角为
所成角为 ,
,
 且侧面
且侧面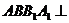 底面
底面 .
.
 (1)证明:点
(1)证明:点 在平面
在平面 上的射影
上的射影 为
为 的中点;
的中点;



 (2)求二面角
(2)求二面角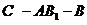 的大小
;
的大小
;
(3)求点 到平面
到平面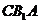 的距离.
的距离.
(1)证明:过B1点作B1O⊥BA。∵侧面ABB1A1⊥底面ABC
∴A1O⊥面ABC ∴∠B1BA是侧面BB1与底面ABC倾斜角
∴∠B1BO= 在Rt△B1OB中,BB1=2,∴BO=
在Rt△B1OB中,BB1=2,∴BO= BB1=1
BB1=1
又∵BB1=AB,∴BO= AB
∴O是AB的中点。
AB
∴O是AB的中点。
即点B1在平面ABC上的射影O为AB的中点 …………4分
(2)连接AB1过点O作OM⊥AB1,连线CM,OC,
∵OC⊥AB,平面ABC⊥平面AA1BB1 ∴OC⊥平面AABB。
∴OM是斜线CM在平面AA1B1B的射影 ∵OM⊥AB1
∴AB1⊥CM ∴∠OMC是二面角C-AB1-B的平面角
在Rt△OCM中,OC=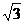 ,OM=
,OM=
∴∠OMC=cosC+sin2
∴二面角C-AB1-B的大小为 …………8分
…………8分
(3)过点O作ON⊥CM,∵AB1⊥平面OCM,∴AB1⊥ON
∴ON⊥平面AB1C。∴ON是O点到平面AB1C的距离

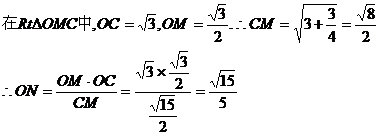
连接BC1与B1C相交于点H,则H是BC1的中点
∴B与C1到平面ACB1的相导。
又∵O是AB的中点 ∴B到平面AB1C的距离
是O到平面AB1C距离的2倍
是G到平面AB1C距离为 …………12分
…………12分
53、(河南省许昌市2008年上期末质量评估)如图,在正三棱柱ABC-A1B1C1中,BB1=BC=2,且M是BC的中点,点N在CC1上.
(Ⅰ)试确定点N的位置,使AB1⊥MN;
(Ⅱ)当AB1⊥MN时,求二面角M-AB1-N的大小.



湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com