
22、已知数列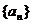 前n项和为
前n项和为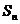 满足:
满足: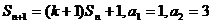
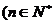 ,k为常数)
,k为常数)
(1)求k的值及数列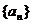 的通项公式;
的通项公式;
(2)设数列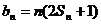 ,求数列
,求数列 的前n项和为
的前n项和为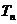 ;
;
(3)试比较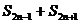 与
与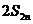 的大小。
的大小。
解:(1)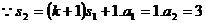

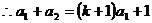
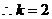
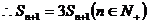
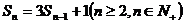
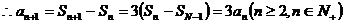
又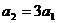
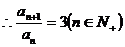

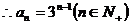
(2)由(1)可知: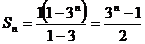
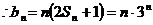
T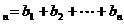
T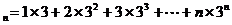
3T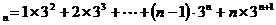
两式相减得 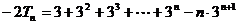
=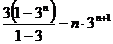
=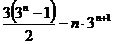
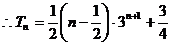
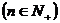
(3)S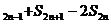
=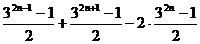
=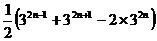 =
=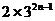 >0 S
>0 S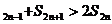
21、设函数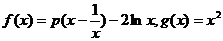 ,
,
(1)若直线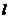 与函数
与函数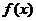 ,
,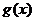
 的图像都相切,且与函数
的图像都相切,且与函数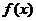 的图像相切于点(1,0),
的图像相切于点(1,0),
求实数P的值。
(2)若函数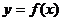 在其定义域内为单调函数,求实数P的取值范围。
在其定义域内为单调函数,求实数P的取值范围。

又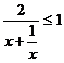
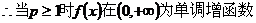
②当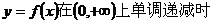
有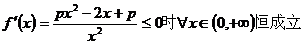
即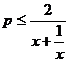 又
又 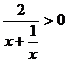
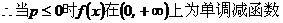
综上.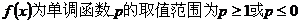
20、在△ABC中,a、b、c分别是角A、B、C的对边,且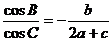 ,
,
(1)求角B的大小;(2)若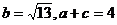 ,求△ABC的面积。
,求△ABC的面积。
解:(1)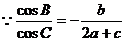 (2)将b=
(2)将b=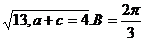 代入
代入
由正弦定理知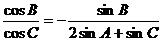
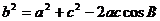
即2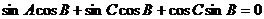 即
即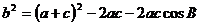
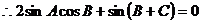
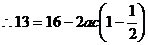
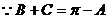
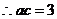
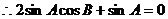

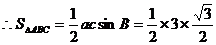
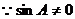 =
=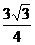

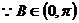
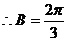

19、已知△ABC的面积S满足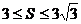 且
且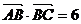 ,
,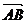 与
与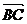 的夹角为
的夹角为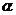
(1)求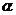 的取值范围; (2)求
的取值范围; (2)求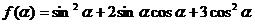 的最小值。
的最小值。

18、已知锐角三角形ABC三个内角为∠A、∠B、∠C,向量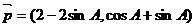 与向量
与向量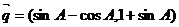 是共线向量,
是共线向量,
求:(1)∠A; (2)函数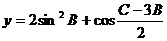 的最大值。
的最大值。
解(1)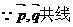
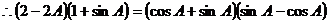
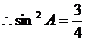
而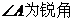 .
.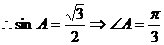
(2)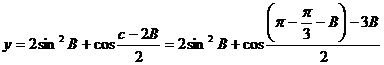
=2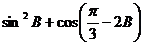
=1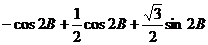
=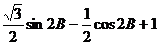
=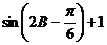
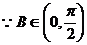
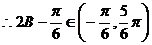
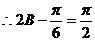
即 B=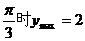
17、已知函数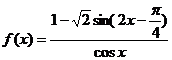 ,(1)求
,(1)求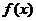 的定义域;
的定义域;
(2)设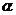 是第四象限的角,且
是第四象限的角,且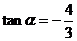 ,求
,求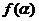 的值。
的值。
解:(1)依题意,cos 解得
解得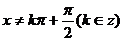
即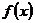 的定义域为
的定义域为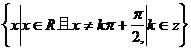
 (2)由
(2)由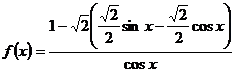
=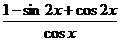 =-2sin
=-2sin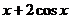
由于是第四象限的角,且tan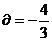
可得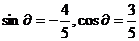
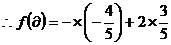 =
=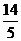
15、
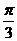 16、 ②③
16、 ②③
13、
3
 14、
-15
14、
-15
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com