
(二)填空是:
6、(07浙江)已知点 在二面角
在二面角 的棱上,点
的棱上,点 在
在 内,且
内,且 .若对于
.若对于 内异于
内异于 的任意一点
的任意一点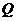 ,都有
,都有 ,则二面角
,则二面角 的大小是 ;
的大小是 ;
7、 (07江苏)正三棱锥
(07江苏)正三棱锥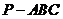 的高为
的高为 ,侧棱与底面
,侧棱与底面 成
成 角,则点
角,则点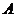 到侧面
到侧面 的距离为_____;
的距离为_____;
8、(07四川)在正三棱柱ABC-A1B1C1中,侧棱长为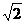 ,底面三角形的边长为1,则BC1与侧面ACC1A1所成的角是 。
,底面三角形的边长为1,则BC1与侧面ACC1A1所成的角是 。
(一)选择题:
1、 (07全国Ⅰ)如图,正四棱柱
(07全国Ⅰ)如图,正四棱柱 中,
中, ,则异面直线
,则异面直线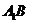 与
与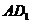 所成角的余弦值为( )
所成角的余弦值为( )
A、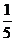 B、
B、 C、
C、 D、
D、
2、(07全国Ⅱ)已知正三棱柱 的侧棱长与底面边长相等,则
的侧棱长与底面边长相等,则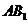 与侧面
与侧面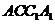 所成角的正弦值等于( )
所成角的正弦值等于( )
A. B.
B.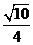 C.
C.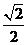 D.
D.
3、 (07江西)如图,正方体
(07江西)如图,正方体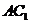 的棱长为
的棱长为 ,过点
,过点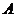 作平面
作平面 的垂线,垂足为点
的垂线,垂足为点 ,则以下命题中,错误的命题是( )
,则以下命题中,错误的命题是( )
 A、点
A、点 是
是 的垂心
的垂心
B、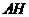 垂直平面
垂直平面
C、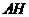 的延长线经过点
的延长线经过点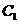
D、直线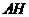 和
和 所成角为
所成角为
4、(07四川)如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
A、BD∥平面CB1D1 B、AC1⊥BD
C、AC1⊥平面CB1D1 D、异面直线AD与CB1角为60°
5、(07重庆)若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成( )
A、 部分 B、
部分 B、 部分 C、
部分 C、 部分 D、
部分 D、 部分
部分
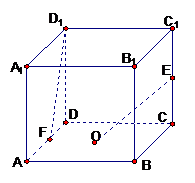 例1、(04天津)如图,在棱长为2的正方体
例1、(04天津)如图,在棱长为2的正方体 中,
中, 是底面
是底面 的中心,
的中心, 分别是
分别是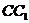 、
、 的
的
中点。那么异面直线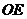 和
和 所成的角的余弦值等于( )
所成的角的余弦值等于( )
A、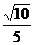 B、
B、 C、
C、 D、
D、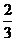
例2、(05上海春)已知直线 及平面
及平面 ,下列命题中的假命题是( )
,下列命题中的假命题是( )
A、若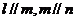 ,则
,则 B、若
B、若 ,则
,则
 C、若
C、若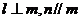 ,则
,则 D、若
D、若 ,则
,则
例3、(06山东)如图5所示,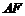 、
、 分别是⊙
分别是⊙ ,⊙
,⊙ 的直径,
的直径, 与两圆所在的平面均垂直,
与两圆所在的平面均垂直, .
. 是⊙
是⊙ 的直径,
的直径, ,
,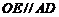 。
。
(I)求二面角 的大小;
的大小;
(II)求直线 与
与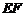 所成的角。
所成的角。
解:(Ⅰ)∵AD与两圆所在的平面均垂直,
∴AD⊥AB, AD⊥AF,故∠BAD是二面角B-AD-F的平面角,
依题意可知,ABCD是正方形,所以∠BAD=450.
即二面角B-AD-F的大小为450;
(Ⅱ)以O为原点,BC、AF、OE所在直线为坐标轴,建立空间直角坐标系(如图所示),则O(0,0,0),A(0,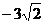 ,0),B(
,0),B( ,0,0),D(0,
,0,0),D(0,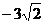 ,8),E(0,0,8),F(0,
,8),E(0,0,8),F(0, ,0)
,0)
 所以,
所以,

设异面直线BD与EF所成角为 ,则
,则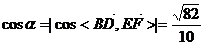
直线BD与EF所成的角为
22、[理科]已知函数 ,其中
,其中
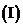 若
若 在x=1处取得极值,求a的值;
在x=1处取得极值,求a的值; 

 求
求 的单调区间;
的单调区间;
(Ⅲ)若 的最小值为1,求a的取值范围。
的最小值为1,求a的取值范围。
解(Ⅰ)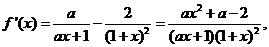
∵ 在x=1处取得极值,∴
在x=1处取得极值,∴ 解得
解得
(Ⅱ)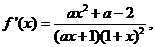
∵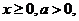 ∴
∴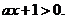
①当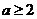 时,在区间
时,在区间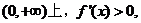 ∴
∴ 的单调增区间为
的单调增区间为
②当 时,
时,
由
∴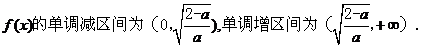
(Ⅲ)当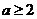 时,由(Ⅱ)①知,
时,由(Ⅱ)①知,
当 时,由(Ⅱ)②知,
时,由(Ⅱ)②知, 在
在 处取得最小值
处取得最小值
综上可知,若 得最小值为1,则a的取值范围是
得最小值为1,则a的取值范围是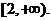
[文科]设函数 ,其中常数
,其中常数
(Ⅰ)讨论 的单调性;
的单调性;
(Ⅱ)若当 时,
时,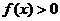 恒成立,求
恒成立,求 的取值范围。
的取值范围。
解: (I)
由 知,当
知,当 时,
时, ,故
,故 在区间
在区间 是增函数;
是增函数;
当 时,
时,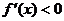 ,故
,故 在区间
在区间 是减函数;
是减函数;
当 时,
时, ,故
,故 在区间
在区间 是增函数。
是增函数。
综上,当 时,
时, 在区间
在区间 和
和 是增函数,在区间
是增函数,在区间 是减函数。
是减函数。
(II)由(I)知,当 时,
时, 在
在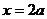 或
或 处取得最小值。
处取得最小值。

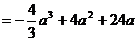 ,
, 
由假设知
 即
即 解得 1<a<6
解得 1<a<6
故 的取值范围是(1,6)
的取值范围是(1,6)
21、等比数列{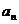 }的前n项和为
}的前n项和为 , 已知对任意的
, 已知对任意的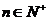 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.
均为常数)的图像上. 

(1)求r的值;
(11)当b=2时,记  求数列
求数列 的前
的前 项和
项和
解:因为对任意的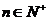 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.所以得
均为常数)的图像上.所以得 ,
,
当 时,
时, ,
, 

当 时,
时, ,
,
又因为{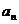 }为等比数列, 所以
}为等比数列, 所以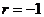 , 公比为
, 公比为 , 所以
, 所以
(2)当b=2时,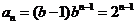 ,
, 
则
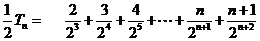


相减,得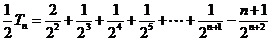


所以
20、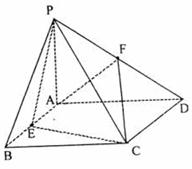 如图,四棱锥
如图,四棱锥 中,
中,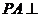 平面
平面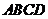 ,四边形
,四边形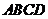 是矩形,
是矩形, 、
、 分别是
分别是 、
、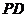 的中点.若
的中点.若 ,
,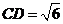 .
.
(Ⅰ)求证: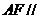 平面
平面 ;
;
(Ⅱ) 求点 到平面
到平面 的距离;
的距离;
(Ⅲ)求直线 平面
平面 所成角的正弦值.
所成角的正弦值.
解:如图建立空间直角坐标系如图,则A(0,0,0),P(0,0,3),D(0,3,0),E( ,0,0),F(0,
,0,0),F(0,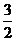 ,
,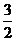 ),C(
),C(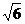 ,3,0)
,3,0)
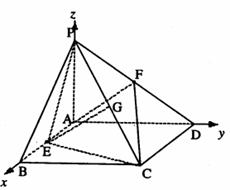 (I)取PC的中点G,连结EG,则G
(I)取PC的中点G,连结EG,则G

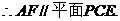
(II)设平面PCE的法向量为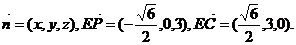

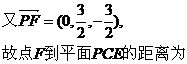

(III)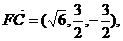
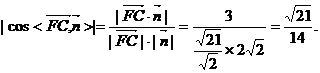
 直线FC与平面PCE所成角的正弦值为
直线FC与平面PCE所成角的正弦值为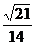 .
.
19、已知函数 的最小正周期为
的最小正周期为 .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)在 中,角
中,角 ,
, ,
, 的对边长分别是
的对边长分别是 ,
, ,
,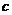 满足
满足 ,求函数
,求函数 的取值范围.
的取值范围.
解:(1)
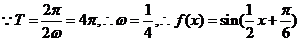
 的单调递增区间为
的单调递增区间为
(2)


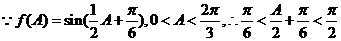
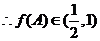
18、已知


(I)若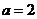 ,求函数
,求函数 在[0,3]的值域
在[0,3]的值域
(Ⅱ)若 的定义域和值域均为
的定义域和值域均为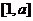 ,求
,求 的值;
的值;
(Ⅲ)若 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的 ,总有
,总有 ,求
,求 的取值范围。
的取值范围。
.解:(1).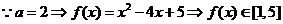 ……………3分
……………3分
(2)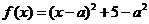
由 的对称轴是
的对称轴是 知函数在
知函数在 递减,故
递减,故 ,
,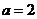 ……………6分
……………6分
(3)由题得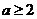 ,故函数在区间
,故函数在区间 上的最小值是
上的最小值是 ,
,
又因为 ,所以函数的最大值是
,所以函数的最大值是
由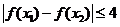 知
知 ,解得
,解得 …………………….12分
…………………….12分
17、甲、乙等四名医务志愿者被随机地分到 、
、 、
、 三个不同的地震灾区服务,每个灾区至少有一名志愿者.
三个不同的地震灾区服务,每个灾区至少有一名志愿者.
(1)求甲、乙两人同时参加 灾区服务的概率;
灾区服务的概率;
(2)求甲、乙两人在同一个灾区服务的概率;
(3)[理科生做,文科生不做]设随机变量 为这四名志愿者中参加
为这四名志愿者中参加 灾区服务的人数,求
灾区服务的人数,求 的分布列.
的分布列.
(1)设甲、乙两人同时参加 灾区服务为事件
灾区服务为事件 ,则
,则 .
.
(2)记甲、乙两人同时参加同一灾区服务为事件 ,那么
,那么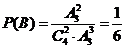 .
.
(3)随机变量 可能取得值为1,2,事件“
可能取得值为1,2,事件“ ”是指有两人同时参加
”是指有两人同时参加 灾区服务,则
灾区服务,则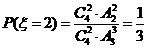 ,所以
,所以 .
.
 分布列是
分布列是
 |
1 |
2 |
 |
 |
 |
16、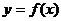 是关于
是关于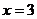 对称的奇函数,
对称的奇函数,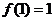 ,
, ,则
,则 = 1
= 1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com