
86、(江苏省常州市北郊中学2008届高三第一次模拟检测)已知数列 满足
满足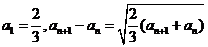 。(
。(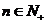 )
)
(1)证明:数列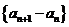 成等差数列;
成等差数列;
(2)设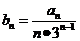 ,数列
,数列 的前
的前 项的和
项的和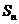 ,求证:
,求证: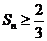 。
。
解:(1)数列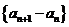 是以
是以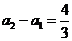 为首项,公差为
为首项,公差为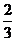 的等差数列;
的等差数列;
(2)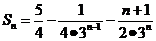
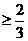
85、(吉林省实验中学2008届高三年级第五次模拟考试)已知: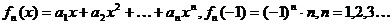
(Ⅰ)求
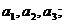
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)求证: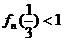
解:(Ⅰ)由已知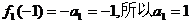 ……………………………………1分
……………………………………1分
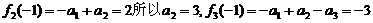 ,所以,
,所以,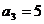 ……3分
……3分
(Ⅱ)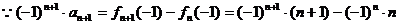
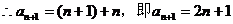
所以对于任意的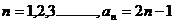 …………………………7分
…………………………7分
(Ⅲ)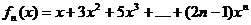
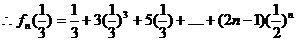 1
1
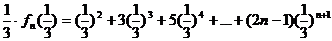 2
2
1-2,得
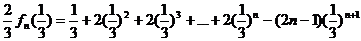 …………9分
…………9分
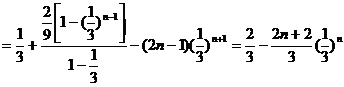
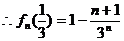 …………11分
又
…………11分
又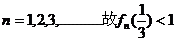 …………12分
…………12分
84、(吉林省吉林市2008届上期末)已知等比数列 的前n项和为Sn=K·2n+m,k≠0,且a1=3.
的前n项和为Sn=K·2n+m,k≠0,且a1=3.
(1)求数列 的通项公式;
的通项公式;
(2)设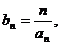 求数列
求数列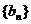 的前n项和Tn.
的前n项和Tn.
(1)解法一:依题意有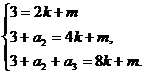 ………………2分
………………2分
解得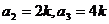
∴公比为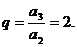 ……………………3分
……………………3分
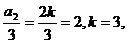 代入①得m=-3,………………5分
代入①得m=-3,………………5分
∴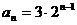 ……………………6分
……………………6分
解法二: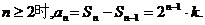 ……………………2分
……………………2分
由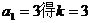
∴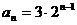 ……………………4分
……………………4分
又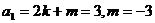 ……………………6分
……………………6分
(2)解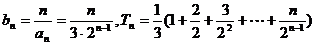 , ④
, ④
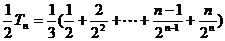 , ⑤ ……………………………………8分
, ⑤ ……………………………………8分
④-⑤得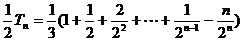 ,
…………………………10分
,
…………………………10分
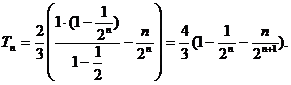 ………………………………12分
………………………………12分
83、(黄家中学高08级十二月月考)已知数列 满足
满足 且对一切
且对一切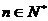 ,有
,有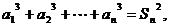
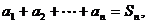 (1)求证:对一切
(1)求证:对一切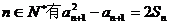
(2)求数列 通项公式. (3)求证:
通项公式. (3)求证: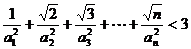
(1) 证明: 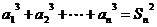 ………. ①
………. ①
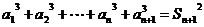 …………②
…………②
② - ①: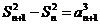
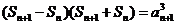
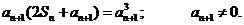
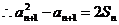 (
(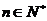 )
)
(2) [解]:由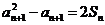 及
及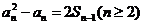
两式相减,得: 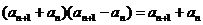
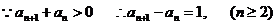

∴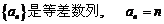 .
.
(3) 证明: ∵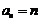
∴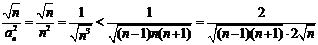
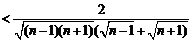
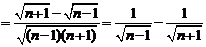
∴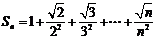
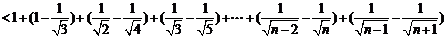
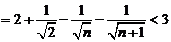
82、(湖南省株洲市2008届高三第二次质检)已知函数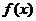 的定义域为
的定义域为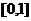 ,且同时满足:对任意
,且同时满足:对任意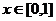 ,总有
,总有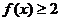 ,
,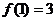 ;
若
;
若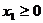 ,
,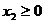 且
且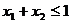 ,则有
,则有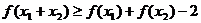 .
.
(1)求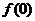 的值;
的值;
(2)试求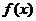 的最大值;
的最大值;
(3)设数列 的前
的前 项和为
项和为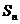 ,且满足
,且满足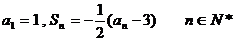 ,
,
求证: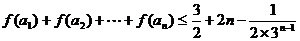 .
.
解:(1)令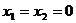 ,则
,则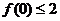 ,又由题意,有
,又由题意,有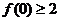
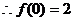 …………………3分
…………………3分
(2)任取 且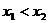 ,则0<
,则0<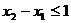
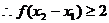
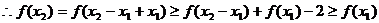
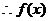 的最大值为
的最大值为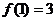 …………………6分
…………………6分
(3)由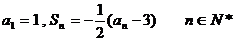
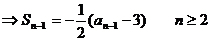
又由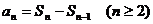
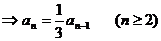
 数列
数列 为首项为1,公比为
为首项为1,公比为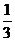 的等比数列,
的等比数列,
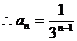 ………8分
………8分
当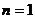 时,
时,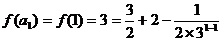 ,不等式成立,
,不等式成立,
当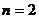 时,
时,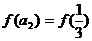
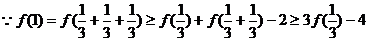 ,
, 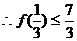
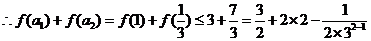 不等式成立
不等式成立
假设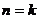 时,不等式成立。
时,不等式成立。
即 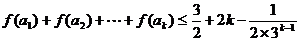
则 当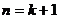 时,
时,
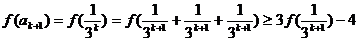
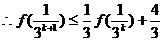
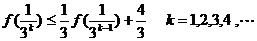
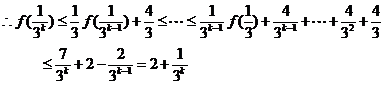

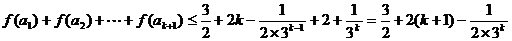
即 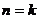 时,不等式成立
时,不等式成立
故
对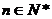 ,原不等式成立。
……………14分
,原不等式成立。
……………14分
81、(湖南省株洲市2008届高三第二次质检)假设A型进口车关税税率在2002年是100%,在2007年是25%,2002年A型进口车每辆价格为64万元(其中含32万元关税税款).
(1)已知与A型车性能相近的B型国产车,2002年每辆价格为46万元,若A型车的价格只受关税降低的影响,为了保证2007年B型车的价格不高于A型车价格的90%,B型车价格要逐年降低,问平均每年至少下降多少万元?
(2)某人在2002年将33万元存入银行,假设银行扣利息税后的年利率为1.8%(5年内不变),且每年按复利计算(上一年的利息计入第二年的本金),那么5年到期时这笔钱连本带息是否一定够买按(1)中所述降价后的B型车一辆?
解:(1)2007年A型车价为32+32×25%=40(万元)
设B型车每年下降d万元,2002,2003……2007年B型车价格为:(公差为-d)
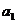 ,
,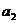 ……
……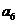 ∴
∴ 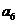 ≤40×90% ∴ 46-5d≤36 d≥2 故每年至少下降2万元…………6分
≤40×90% ∴ 46-5d≤36 d≥2 故每年至少下降2万元…………6分
(2)2007年到期时共有钱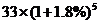 >33(1+0.09+0.00324+……)=36.07692>36(万元)
>33(1+0.09+0.00324+……)=36.07692>36(万元)
故5年到期后这笔钱够买一辆降价后的B型车 …………………12分
80、(湖南省岳阳市2008届高三第一次模拟)已知点(an,an-1)在曲线f(x)=上, 且a1=1.
(1)求f(x)的定义域;
(2)求证: 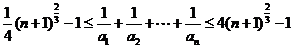 (n∈N*)
(n∈N*)
(3)求证: 数列{an}前n项和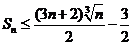 (n≥1, n∈N*)
(n≥1, n∈N*)
解:(1) 由f(x)=知x满足: x2+ ≥0, ∴ ≥0 , ∴≥0
∴ ≥0, 故x>0, 或x≤-1.
f(x)定义域为: (-∞, -1]∪(0,+∞)
(2)∵ an+12=an2+ , 则an+12-an2 = 于是有: 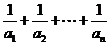 =
an+12-a12 =
an+12-1
=
an+12-a12 =
an+12-1
要证明: 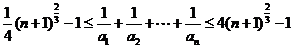
只需证明: 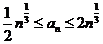 ( *) 下面使用数学归纳法证明:
( *) 下面使用数学归纳法证明:
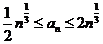 (n≥1,n∈N*) ①在n=1时, a1=1, <a1<2, 则n=1时 (* )式成立.
(n≥1,n∈N*) ①在n=1时, a1=1, <a1<2, 则n=1时 (* )式成立.
②假设n=k时, 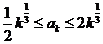 成立, 由
成立, 由 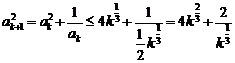
要证明: 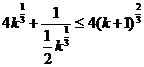 只需2k+1≤
只需2k+1≤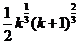 只需(2k+1)3≤8k(k+1)2
只需(2k+1)3≤8k(k+1)2

只需证: 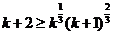 , 只需证: 4k2+11k+8>0, 而4k2+11k+8>0在k≥1时恒成立. 于是:
, 只需证: 4k2+11k+8>0, 而4k2+11k+8>0在k≥1时恒成立. 于是: 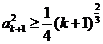 .
因此
.
因此 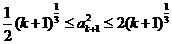 得证.
得证.
综合①②可知( *)式得证, 从而原不等式成立.
(3)要证明: 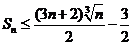 ,
,
由(2)可知只需证: 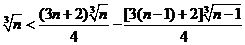 (n≥2) (** )
(n≥2) (** )
下面用分析法证明: (**)式成立. 要使(**)成立,
只需证: (3n-2)>(3n-1)
即只需证: (3n-2)3n>(3n-1)3(n-1), 只需证:2n>1. 而2n>1在n≥1时显然成立,故(**)式得证.
于是由(**)式可知有: + +…+≤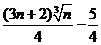
因此有: Sn=a1+a2+…+an≤1+2(+ +…+) = 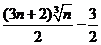
79、(湖南省雅礼中学2008年高三年级第六次月考)容器A内装有6升质量分数为20%的盐水溶液,容器B内装有4升质量分数为5%的盐水溶液,先将A内的盐水倒1升进入B内,再将B内的盐水倒1升进入A内,称为一次操作;这样反复操作n次,A、B容器内的盐水的质量分数分别为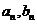 ,
,
(I)问至少操作多少次,A、B两容器内的盐水浓度之差小于1%?(取lg2=0.3010,lg3=0.4771)
(Ⅱ)求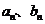 的表达式,并求
的表达式,并求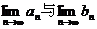 的值. 雅创教育网免费注册免费下载
的值. 雅创教育网免费注册免费下载
解:(1)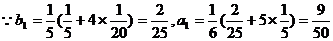 ;
;
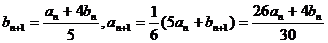 ;
;
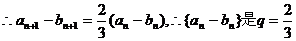 的等比数列,
的等比数列,
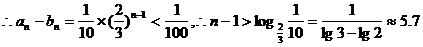 ,
,
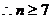 ,故至少操作7次;
,故至少操作7次;
(2)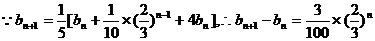
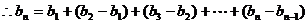
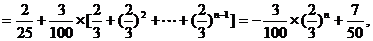
而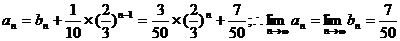 .
.
78、(湖南省长沙市一中2008届高三第六次月考)数列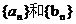 ,由下列条件确定:①a1<0,b1<0.②当k≥2时,ak和bk满足下列条件:当
,由下列条件确定:①a1<0,b1<0.②当k≥2时,ak和bk满足下列条件:当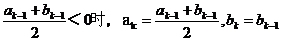 .
.
(1)若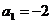 ,
,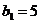 ,分别写出{an}、{bn}的前四项.
,分别写出{an}、{bn}的前四项.
(2)证明数列{ak-bk}是等比数列.
(3)设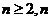 是满足b1>b2>…>bn的最大整数时,用a1、b1表示n满足的条件.
是满足b1>b2>…>bn的最大整数时,用a1、b1表示n满足的条件.
解:(1)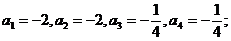
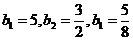 ………………………………………………………………………(3分)
………………………………………………………………………(3分)
(2)当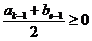 时,
时,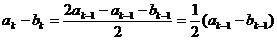
当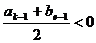 时,
时,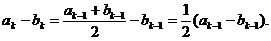
又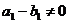 ,∴数列
,∴数列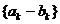 是等比数列. ……………………………………………(9分)
是等比数列. ……………………………………………(9分)
(3)当b1>b2>…>bn(n≥2)时,bk≠bk-1(2≤k≤n).
由(2)知: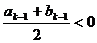 不成立,
不成立,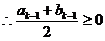 .
.
从而对于2≤k≤n有ak=ak-1,bk=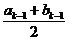
于是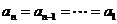 ……………………………………………………………………(11分)
……………………………………………………………………(11分)
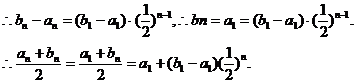
若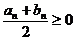 ,则
,则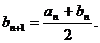
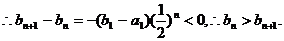
这与 是满足b1>b2>…>bn(n≥2)的最大整数矛盾.
是满足b1>b2>…>bn(n≥2)的最大整数矛盾.
∴n是满足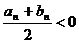 的最小整数.
的最小整数.
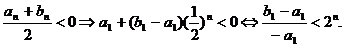
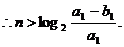
 n是满足大于
n是满足大于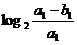 的最小整数.…………………………(13分)
的最小整数.…………………………(13分)
77、(湖南省十二校2008届高三第一次联考)已知二次函数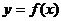 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为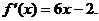 数列{
数列{ }的前n项和为
}的前n项和为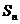 ,点
,点 均在函数
均在函数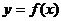 的图像上.
的图像上.
(I)求数列{ }的通项公式;
}的通项公式;
(II)设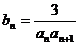 ,
,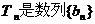 的前n项和,求使得
的前n项和,求使得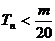 对所有
对所有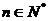 都成立的最小正整数m.
都成立的最小正整数m.
解:(I)设这二次函数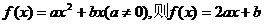 ,
,
由于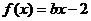 ,得
,得
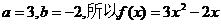 …………2分
…………2分
又因为点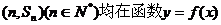 的图像上,
的图像上,
所以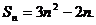
当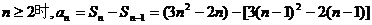
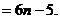 …………6分
…………6分
(II)由(I)得知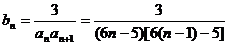
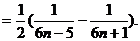 …………7分
…………7分
故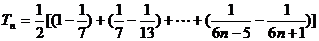
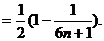 …………9分
…………9分
因此,要使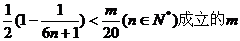 ,必须且仅须满足
,必须且仅须满足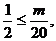
即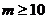 , …………11分
, …………11分
所以满足要求的最小正整数m为10。 …………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com