
(二)填空是:
4、(07全国Ⅰ16)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为2,则该三角形的斜边长为 ;
5、(07安徽15)在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是 (写出所有正确结论的编号).
①矩形;
②不是矩形的平行四边形;
③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;
④每个面都是等边三角形的四面体;
⑤每个面都是直角三角形的四面体。
(一)选择题:
1、(07湖南)棱长为1的正方体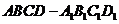 的8个顶点都在球
的8个顶点都在球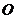 的表面上,
的表面上,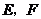 分别是棱
分别是棱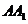 ,
,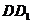 的中点,则直线
的中点,则直线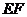 被球
被球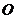 截得的线段长为( )
截得的线段长为( )
A、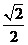 B、
B、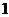 C、
C、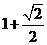 D、
D、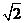
2、(07安徽)半径为1的球面上的四点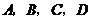 是正四面体的顶点,则
是正四面体的顶点,则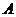 与
与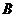 两点间的球面距离为( )
两点间的球面距离为( )
A、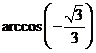 B、
B、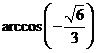 C、
C、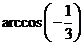 D、
D、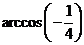
3、(07福建)顶点在同一球面上的正四棱柱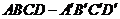 中,
中,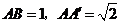 ,则
,则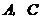 两点间的球面距离为( )
两点间的球面距离为( )
A、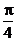 B、
B、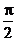 C、
C、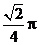 D、
D、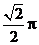
例1、(07山东)下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A、①② B、①③ C、①④ D、②④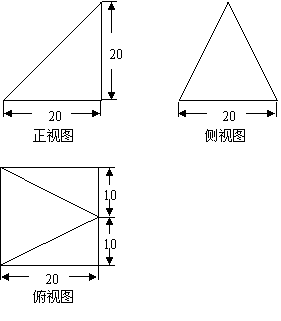
例2、(07全国Ⅰ)已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
A、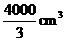
B、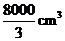
C、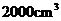
D、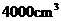
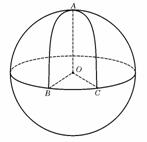 例3、(07四川)设球O的半径是1,A、B、C是球面上三点,已知A到B、C两点的球面距离都是
例3、(07四川)设球O的半径是1,A、B、C是球面上三点,已知A到B、C两点的球面距离都是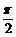 ,且三面角B-OA-C的大小为
,且三面角B-OA-C的大小为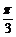 ,则从A点沿球面经B、C两点再回到A点的最短距离是( )
,则从A点沿球面经B、C两点再回到A点的最短距离是( )
A、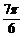 B、
B、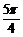 C、
C、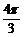 D、
D、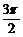
(二)解答题:
6、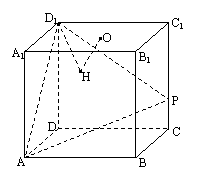 (04江苏)在棱长为4的正方体
(04江苏)在棱长为4的正方体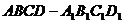 中,
中,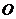 是正方形
是正方形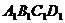 的中心,点
的中心,点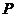 在棱
在棱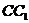 上,且
上,且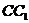
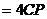 。
。
(Ⅰ)求直线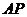 与平面
与平面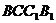 所成的角的大小(结果用反三角函数值表示);
所成的角的大小(结果用反三角函数值表示);
(Ⅱ)设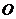 点在平面
点在平面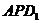 上的射影是
上的射影是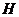 ,求证:
,求证: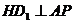 ;
;
(Ⅲ)求点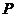 到平面
到平面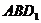 的距离。
的距离。
解(1)
(2)略
(3)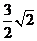
(一)选择题:
1、(07北京)平面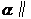 平面
平面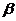 的一个充分条件是( )
的一个充分条件是( )
A、存在一条直线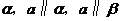 B、存在一条直线
B、存在一条直线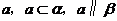
C、存在两条平行直线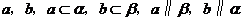
D、存在两条异面直线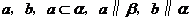
2、(07江苏)已知两条直线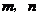 ,两个平面
,两个平面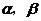 .给出下面四个命题:
.给出下面四个命题:
①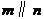 ,
,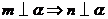 ;②
;②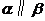 ,
,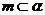 ,
,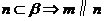 ;
;
③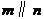 ,
,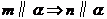 ;④
;④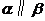 ,
,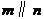 ,
,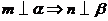 .
.
其中正确命题的序号是( )
A、①、③ B、②、④ C、①、④ D、②、③
3、(07天津)设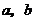 为两条直线,
为两条直线,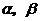 为两个平面,下列四个命题中,正确的命题是( )
为两个平面,下列四个命题中,正确的命题是( )
A、若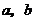 与
与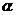 所成的角相等,则
所成的角相等,则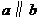 B、若
B、若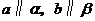 ,
,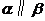 ,则
,则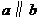
C、若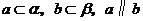 ,则
,则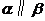 D、若
D、若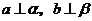 ,
,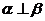 ,则
,则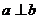
4、(07陕西)已知平面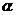
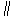 平面
平面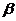 ,直线
,直线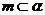 ,直线
,直线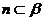 ,点
,点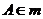 ,点
,点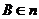 ,记点
,记点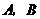 之间的距离为
之间的距离为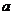 ,点
,点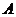 到直线
到直线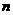 的距离为
的距离为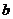 ,直线
,直线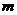 和
和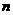 的距离为
的距离为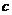 ,则( )
,则( )
A、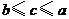 B、
B、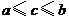 C、
C、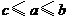 D、
D、 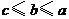
5、(07福建)已知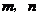 为两条不同的直线,
为两条不同的直线,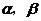 为两个不同的平面,则下列命题中正确的是( )
为两个不同的平面,则下列命题中正确的是( )
A、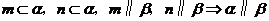 B、
B、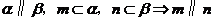
C、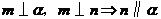 D、
D、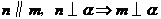
例1、(05上海春)有下列三个命题:
①分别在两个平行平面内的两条直线一定是异面直线;②垂直于同一平面的两条直线是平行直线;③过平面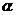 的一条斜线有一个平面与平面
的一条斜线有一个平面与平面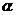 垂直。其中正确的命题的个数为( )
垂直。其中正确的命题的个数为( )
 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3
例2、(06北京)如图,在底面为平行四边形的四棱锥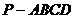 中,
中,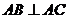 ,
,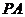 ⊥平面
⊥平面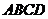 ,且
,且 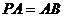 ,点
,点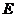 是
是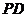 的中点.。
的中点.。
(Ⅰ)求证: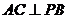 ;
;
(Ⅱ)求证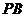 //平面
//平面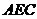 ;
;
(Ⅲ)求二面角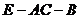 的大小。
的大小。
解法一:
(Ⅰ)∵PA⊥平面 ABCD,
∴AB 是 PB 在平面 ABCD 上的射影.
又∵AB⊥AC,AC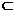 平面ABCD,
平面ABCD,
∴AC⊥PB.
(Ⅱ)连接BD,与 AC 相交于 O,连接 EO.
∵ABCD 是平行四边形,
∴O 是 BD 的中点
又 E 是 PD 的中点
∴EO∥PB.
又 PB 平面 AEC,EO
平面 AEC,EO 平面 AEC,
平面 AEC,
∴PB∥平面 AEC.
(Ⅲ)取 BC 中点 G,连接 OG,则点 G 的坐标为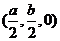 ,
,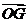 =
=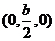 .
.
又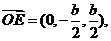
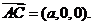
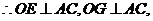
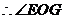 是二面角
是二面角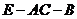 的平面角
的平面角

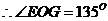
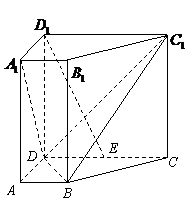
 二面角E-AC-B的大小为
二面角E-AC-B的大小为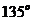 。
。
例3、(07山东)如图,在直四棱柱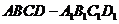 中,已知
中,已知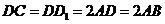 ,
,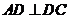 ,
,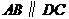 .
.
(Ⅰ)设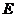 是
是 的中点,求证:
的中点,求证: 平面
平面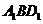 ;
;
(Ⅱ)求二面角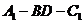 的余弦值.
的余弦值.
解法一:
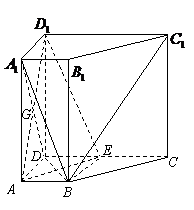 (Ⅰ)连结
(Ⅰ)连结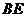 ,则四边形
,则四边形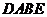 为正方形,
为正方形,
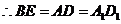 ,且
,且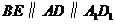 ,
,
 四边形
四边形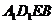 为平行四边形.
为平行四边形.
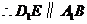 .
.
又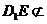 平面
平面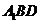 ,
,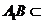 平面
平面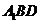 ,
,
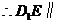 平面
平面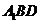 .
.
(Ⅱ)以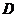 为原点,
为原点,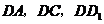 所在直线分别为
所在直线分别为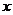 轴,
轴,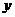 轴,
轴,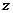 轴建立如图所示的空间直角坐标系,不妨设
轴建立如图所示的空间直角坐标系,不妨设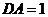 ,则
,则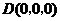 ,
, ,
,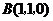 ,
,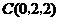 ,
,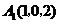 ,
,

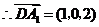 ,
, ,
,
设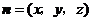 为平面
为平面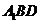 的一个法向量.
的一个法向量.
由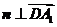 ,
,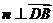 ,
,
得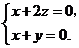
取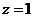 ,则
,则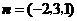 .
.
又 ,
, ,
,
设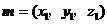 为平面
为平面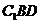 的一个法向量,
的一个法向量,
由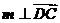 ,
,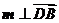 ,
,
得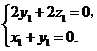
取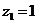 ,则
,则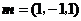 ,
,
设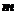 与
与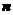 的夹角为
的夹角为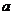 ,二面角
,二面角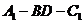 为
为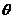 ,显然
,显然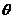 为锐角,
为锐角,
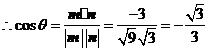 .
.
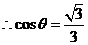 ,
,
即所求二面角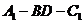 的余弦为
的余弦为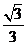 .
.
解法二:
(Ⅰ)以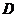 为原点,
为原点,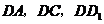 所在直线分别为
所在直线分别为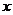 轴,
轴,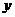 轴,
轴,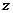 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
设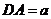 ,由题意知:
,由题意知:

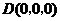 ,
,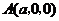 ,
,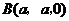 ,
, ,
,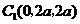 ,
,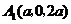 ,
,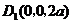 ,
,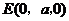 .
.
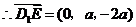 ,
,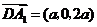 ,
,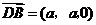 ,
,
又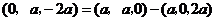 ,
,
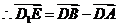 .
.
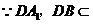 平面
平面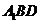 ,
,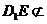 平面
平面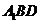 ,
,
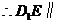 平面
平面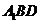 .
.
(Ⅱ)取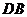 的中点
的中点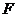 ,
,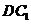 的中点
的中点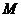 ,连结
,连结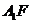 ,
,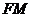 ,
,
由(Ⅰ)及题意得知:
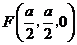 ,
,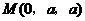 ,
,
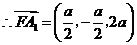 ,
,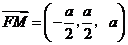 ,
,
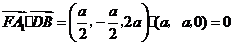 ,
,
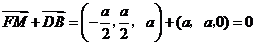 .
.
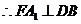 ,
,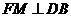 ,
,
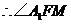 为所求二面角的平面角.
为所求二面角的平面角.
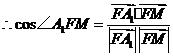
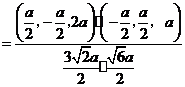
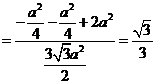 .
.
所以二面角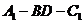 的余弦值为
的余弦值为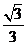 .
.
解法三:
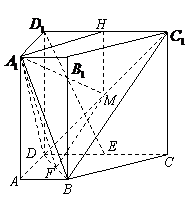 (Ⅰ)证明:如解法一图,连结
(Ⅰ)证明:如解法一图,连结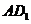 ,
,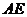 ,
,
设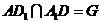 ,
,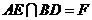 ,连结
,连结 ,
,
由题意知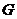 是
是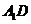 的中点,又
的中点,又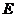 是
是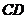 的中点,
的中点,
 四边形
四边形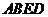 是平行四边形,故
是平行四边形,故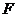 是
是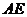 的中点,
的中点,
 在
在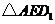 中,
中,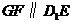 ,
,
又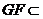 平面
平面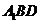 ,
,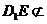 平面
平面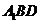 ,
,
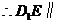 平面
平面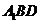 .
.
(Ⅱ)如图,在四边形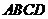 中,设
中,设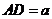 ,
,
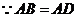 ,
,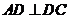 ,
,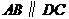 ,
,
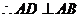 .
.
故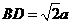 ,由(Ⅰ)得
,由(Ⅰ)得
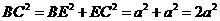 ,
,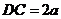 ,
,
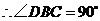 ,即
,即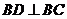 .
.
又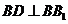 ,
,
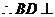 平面
平面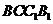 ,又
,又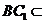 平面
平面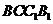 ,
,
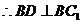 ,
,
取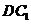 的中点
的中点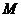 ,连结
,连结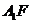 ,
,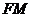 ,
,
由题意知: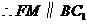 ,
,
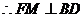 .
.
又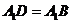 ,
,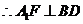 .
.
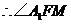 为二面角
为二面角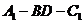 的平面角.
的平面角.
连结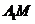 ,在
,在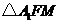 中,
中,
由题意知:
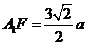 ,
,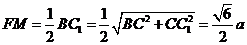 ,
,
取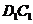 的中点
的中点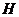 ,连结
,连结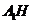 ,
,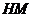 ,
,
在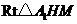 中,
中,
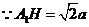 ,
,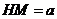 ,
,
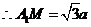 .
.
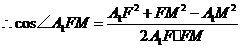
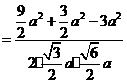
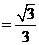 .
.
 二面角
二面角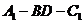 的余弦值为
的余弦值为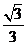 .
.
(二)填空是:
2、(05山东)在平面几何里,有勾股定理:“设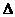
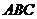 的两边
的两边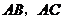 互相垂直,则有,
互相垂直,则有,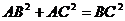 。”拓展到空间,类比平面几何的定理,研究三棱锥的侧面面积与底面面积的关系,可以得出的正确结论是:“设三棱锥
。”拓展到空间,类比平面几何的定理,研究三棱锥的侧面面积与底面面积的关系,可以得出的正确结论是:“设三棱锥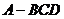 的三个侧面
的三个侧面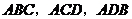 两两相互垂直,则
。
两两相互垂直,则
。
 (三)解答题:
(三)解答题:
3、(07海南)如图,在三棱锥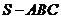 中,侧面
中,侧面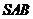 与侧面
与侧面 均为等边三角形,
均为等边三角形,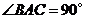 ,
,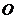 为
为 中点.
中点.
(Ⅰ)证明: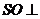 平面
平面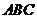 ;
;
(Ⅱ)求二面角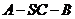 的余弦值。
的余弦值。
证明:
(Ⅰ)由题设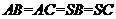
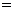
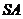 ,连结
,连结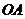 ,
,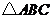 为等腰直角三角形,所以
为等腰直角三角形,所以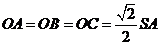 ,且
,且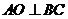 ,又
,又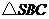 为等腰三角形,故
为等腰三角形,故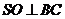 ,且
,且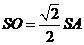 ,从而
,从而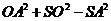 .
.
所以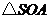 为直角三角形,
为直角三角形,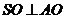 .
.
又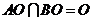 .
.
所以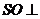 平面
平面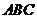 .
.
(Ⅱ)解法一:
取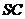 中点
中点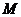 ,连结
,连结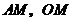 ,由(Ⅰ)知
,由(Ⅰ)知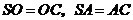 ,得
,得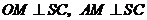 .
.
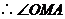 为二面角
为二面角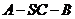 的平面角.
的平面角.
由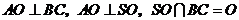 得
得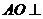 平面
平面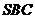 .
.
所以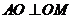 ,又
,又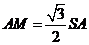 ,
,
故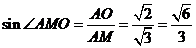 .
.
所以二面角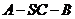 的余弦值为
的余弦值为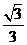 .
.
解法二:
以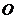 为坐标原点,射线
为坐标原点,射线 分别为
分别为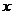 轴、
轴、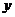 轴的正半轴,建立如图的空间直角坐标系
轴的正半轴,建立如图的空间直角坐标系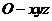 .
.
设 ,则
,则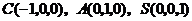 .
.

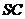 的中点
的中点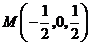 ,
,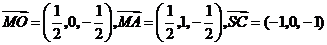 .
.
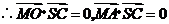 .
.
故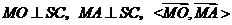 等于二面角
等于二面角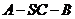 的平面角.
的平面角.
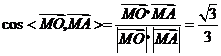 ,
,
所以二面角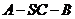 的余弦值为
的余弦值为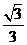 .
.
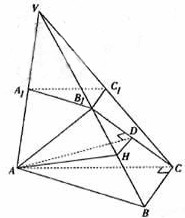
4、(06山东)如图 ,已知平面平行于三棱锥
,已知平面平行于三棱锥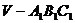 的底面
的底面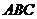 ,等边
,等边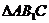 所在的平面与底面
所在的平面与底面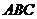 垂直,且
垂直,且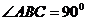 ,设
,设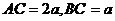 。
。
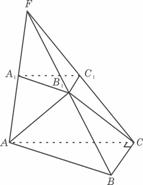 (1)求证直线
(1)求证直线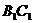 是异面直线与
是异面直线与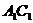 的公垂线;
的公垂线;
(2)求点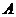 到平面
到平面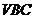 的距离;
的距离;
(3)求二面角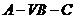 的大小。
的大小。
解法1:
(Ⅰ)证明:∵平面
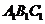 ∥平面
∥平面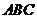 ,
,
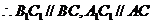
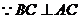
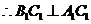
又∵平面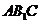 ⊥平面
⊥平面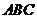 ,平面
,平面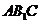 ∩平面
∩平面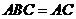 ,
,
∴ ⊥平面
⊥平面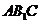 ,
,
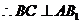
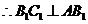 ,
,
又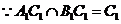 ,
,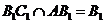 .
.
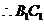 为
为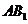 与
与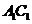 的公垂线.
的公垂线.
(Ⅱ)解法1:过A作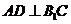 于D,
于D,
∵△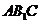 为正三角形,
为正三角形,
∴D为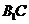 的中点.
的中点.
∵BC⊥平面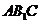
∴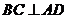 ,
,
又 ,
,
∴AD⊥平面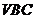 ,
,
∴线段AD的长即为点A到平面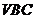 的距离.
的距离.
在正△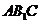 中,
中,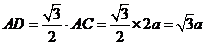 .
.
∴点A到平面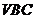 的距离为
的距离为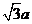 .
.
解法2:取AC中点O连结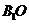 ,则
,则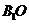 ⊥平面
⊥平面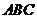 ,且
,且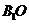 =
=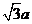 .
.
由(Ⅰ)知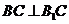 ,设A到平面
,设A到平面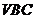 的距离为x,
的距离为x,
 ,
,
即 ,解得
,解得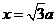 .
.
即A到平面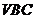 的距离为
的距离为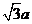 .
.
则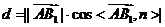
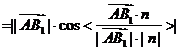
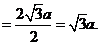
所以,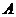 到平面
到平面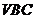 的距离为
的距离为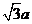 .
.
(III)过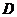 点作
点作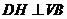 于
于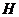 ,连
,连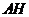 ,由三重线定理知
,由三重线定理知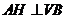
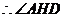 是二面角
是二面角 的平面角。
的平面角。
在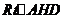 中,
中,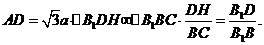
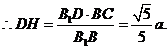
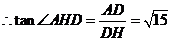 。
。
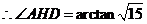 。
。
所以,二面角 的大小为arctan
的大小为arctan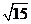 .
.
解法二:
取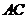 中点
中点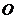 连
连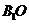 ,易知
,易知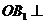 底面
底面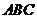 ,过
,过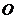 作直线
作直线 交
交 。
。
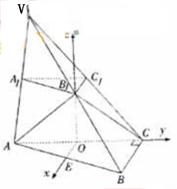 取
取 为空间直角坐标系的原点,
为空间直角坐标系的原点,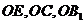 所在直线分别为
所在直线分别为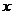 轴,
轴,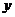 轴,
轴,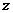 轴建立如图所示的空间直角坐标系。则
轴建立如图所示的空间直角坐标系。则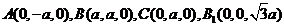 。
。
(I)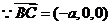 ,
,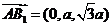 ,
,
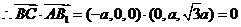 ,
,
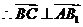 。
。
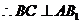
又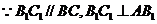
由已知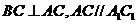 。
。
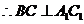 ,
,
而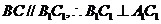 。
。
又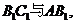
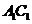 显然相交,
显然相交,
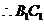 是
是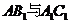 的公垂线。
的公垂线。
(II)设平面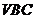 的一个法向量
的一个法向量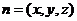 ,
,
又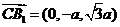
由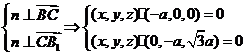
取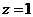 得
得 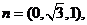
点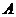 到平面
到平面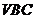 的距离,即
的距离,即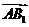 在平面
在平面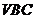 的法向量
的法向量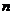 上的投影的绝对值。
上的投影的绝对值。
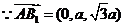 ,设所求距离为
,设所求距离为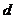 。
。
则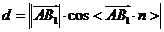

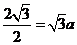
所以,A到平面VBC的距离为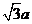 .
.
(III)设平面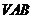 的一个法向量
的一个法向量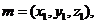
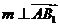
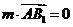
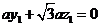
由
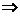
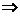
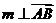
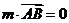
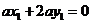
取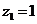
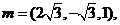

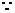 二面角
二面角 为锐角,
为锐角,
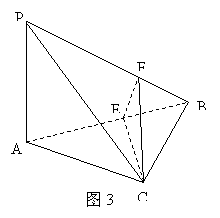 所以,二面角
所以,二面角 的大小为
的大小为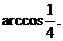
5、(05广东)如图3所示,在四面体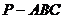 中,已知
中,已知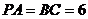 ,
,
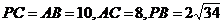 .
.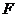 是线段
是线段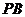 上一点,
上一点,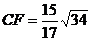 ,点
,点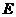 在线段
在线段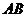 上,且
上,且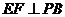 .
.
(Ⅰ)证明: ;
;
(Ⅱ)求二面角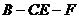 的大小.
的大小.
[答案]
(Ⅰ)证明:在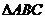 中, ∵
中, ∵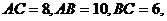
∴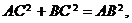
∴△PAC是以∠PAC为直角的直角三角形,
同理可证,△PAB是以∠PAB为直角的直角三角形,
△PCB是以∠PCB为直角的直角三角形.
在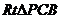 中,∵
中,∵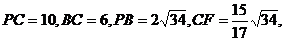
∴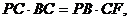 ∴
∴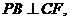
又∵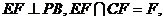
∴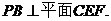
(II)解法一:由(I)知PB⊥CE,PA⊥平面ABC
∴AB是PB在平面ABC上的射影,故AB⊥CE
∴CE⊥平面PAB,而EF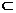 平面PAB,
平面PAB,
∴EF⊥EC,
故∠FEB是二面角B-CE-F的平面角,
∵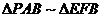
∴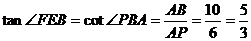 ,
,
∴二面角B-CE-F的大小为 .
.
解法二:如图,以C点的原点,CB、CA为x、y轴,
建立空间直角坐标系C-xyz,则
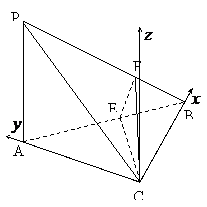
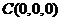 ,
,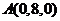 ,
,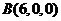 ,
,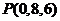 ,
,
∵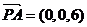 为平面ABC的法向量,
为平面ABC的法向量,
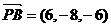 为平面ABC的法向量,
为平面ABC的法向量,
∴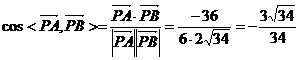 ,
,
∴二面角B-CE-F的大小为 .
.
(一)选择题:
1、(05天津)设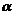 、
、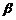 、
、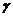 为平面,为
为平面,为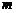 、
、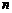 、
、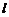 直线,则
直线,则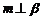 的一个充分条件是
的一个充分条件是
A、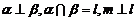 B、
B、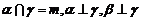
C、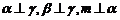 D、
D、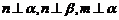
 例1、(05北京春)如图,正三角形
例1、(05北京春)如图,正三角形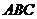 的边长为3,过其中心
的边长为3,过其中心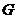 作
作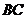 边的平行线,分别交
边的平行线,分别交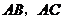 于
于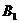 、
、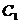 。将
。将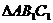 沿
沿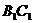 折起到
折起到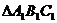 的位置,使点
的位置,使点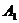 在平面
在平面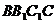 上的射影恰是线段
上的射影恰是线段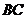 的中点
的中点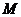 。求:(1)二面角
。求:(1)二面角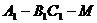 的大小;(2)异面直线
的大小;(2)异面直线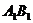 与
与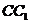 所成角的大小(用反三角函数表示)。
所成角的大小(用反三角函数表示)。
例2、(04重庆)设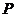 是
是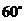 的二面角
的二面角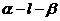 内一点,
内一点,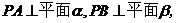
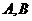 分别为垂足,
分别为垂足,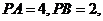 则
则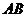 的长为:( )
的长为:( )
A、 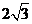 B、
B、 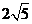 C、
C、 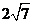 D、
D、
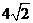
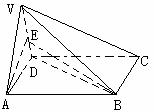 例3、(05全国Ⅲ)如图,在四棱锥
例3、(05全国Ⅲ)如图,在四棱锥 中,底面
中,底面 是正方形,
是正方形,
侧面 是正三角形,平面
是正三角形,平面 ⊥底面
⊥底面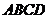 。
。
(Ⅰ)证明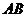 ⊥平面
⊥平面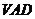 ;
;
(Ⅱ)求面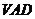 与面
与面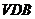 所成的二面角的大小。
所成的二面角的大小。
方法一:(Ⅰ)证明:

(Ⅱ)解:取VD的中点E,连结AE,BE
∵VAD是正三角形
∴AE⊥VD,AF=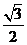 AD
AD
∵AB⊥平面VAD ∴AB⊥AE
又由三垂线定理知BE⊥VD
因此,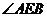 是所求二面角的平面角
是所求二面角的平面角
于是,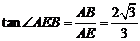
即得所求二面角的大小为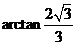
方法二:以D为坐标原点,建立如图所示的坐标系。
(Ⅰ)证明:不妨设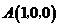 ,则
,则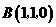 ,
,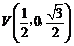
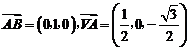
由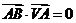 ,得
,得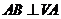
又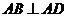 ,因而
,因而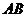 与平面
与平面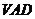 内两条相交直线
内两条相交直线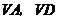 都垂直。
都垂直。
∴ 平面
平面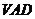
(Ⅱ)解:设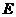 为
为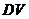 中点,则
中点,则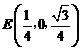
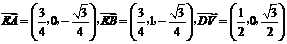
由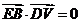 ,得
,得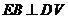 ,又
,又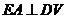
因此,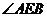 是所求二面角的平面角。
是所求二面角的平面角。
∵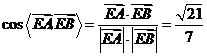
∴解得所求二面角的大小为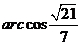 。
。
(三)解答题:
9、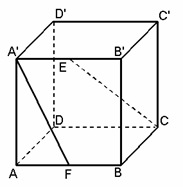 (07上海春)如图,在棱长为2的正方体
(07上海春)如图,在棱长为2的正方体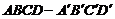 中,
中,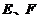 分别是
分别是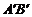 和
和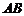 的中点,求异面直线
的中点,求异面直线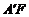 与
与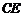 所成角的大小 (结果用反三角函数值表示)。
所成角的大小 (结果用反三角函数值表示)。
[解法一] 如图建立空间直角坐标系 …… 2分
…… 2分
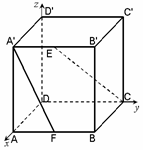 由题意可知
由题意可知


 …… 6分
…… 6分
设直线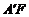 与
与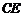 所成角为
所成角为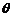 ,则
,则
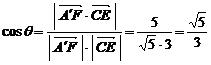
 …… 10分
…… 10分
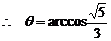 ,
,
即异面直线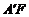 与
与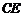 所成角的大小为
所成角的大小为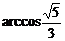
 …… 12分
…… 12分
[解法二] 连接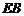 ,
…… 2分
,
…… 2分
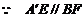 ,且
,且 ,
,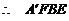 是平行四边形,则
是平行四边形,则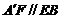 ,
,
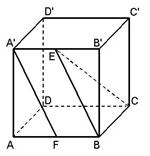
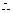 异面直线
异面直线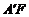 与
与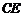 所成的角就是
所成的角就是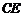 与
与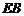 所成的角
所成的角 …… 6分
…… 6分
由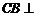 平面
平面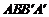 ,得
,得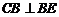

在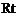 △
△ 中,
中,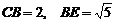 ,则
,则
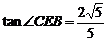 ,
…… 10分
,
…… 10分
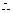
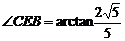

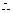 异面直线
异面直线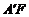 与
与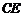 所成角的大小为
所成角的大小为
 …… 12分
…… 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com