
96、(江西省鹰潭市2008届高三第一次模拟)已知函数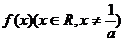 满足
满足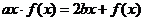 ,
,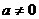 ,
,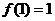 ;且使
;且使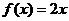 成立的实数
成立的实数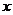 只有一个。
只有一个。
(Ⅰ)求函数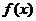 的表达式;
的表达式;
(Ⅱ)若数列 满足
满足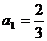 ,
,
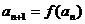 ,
,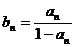 ,
,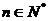 ,证明数列
,证明数列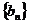 是等比数列,并求出
是等比数列,并求出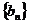 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,如果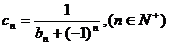 ,
,
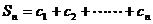 ,证明:
,证明: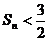 ,
,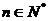 。
。
解:(Ⅰ)由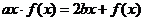 ,
,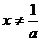 ,
,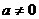 ,得
,得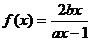 .…1分
.…1分
由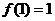 ,得
,得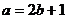 .…………2分
.…………2分
由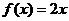 只有一解,即
只有一解,即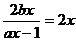 ,也就是
,也就是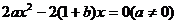 只有一解,
只有一解,
∴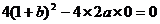 ∴
∴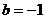 .…………3分
.…………3分
∴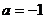 .故
.故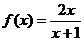 .…………………4分
.…………………4分
(Ⅱ)解法一:∵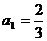 ,
,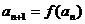 ,∴
,∴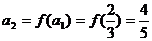 ,
,
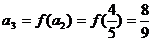 ,
,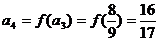 ,……………5分
,……………5分
猜想,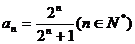 .……………6分
.……………6分
下面用数学归纳法证明:
10 当n=1时,左边=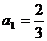 ,右边=
,右边=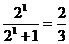 ,∴命题成立. ……………7分
,∴命题成立. ……………7分
20 假设n=k时,命题成立,即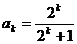 ;当 n=k+1时,
;当 n=k+1时,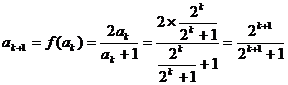 ,
,
∴当 n=k+1时,命题成立. ………………8分
由10,20可得,当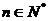 时,有
时,有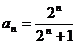 .……………9分
.……………9分
∵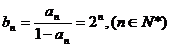 ,∴
,∴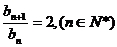
∴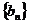 是首项为
是首项为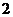 ,公比为
,公比为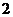 的等比数列,其通项公式为
的等比数列,其通项公式为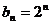 .………10分
.………10分
解法二:∵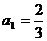 ,
,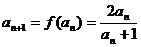 ∴
∴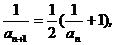 ………5分
………5分
即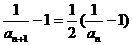 ,………8分
,………8分
∴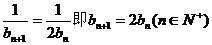 ………9分
………9分
 ,
,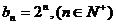 ………10分
………10分
(Ⅲ)当 为偶数时,
为偶数时,
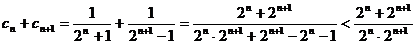
即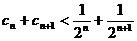 ………………12分
………………12分
∴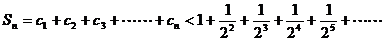
即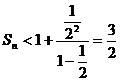 .…………………14分
.…………………14分
95、(江苏省盐城市2008届高三六校联考)已知函数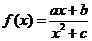 是定义在R上的奇函数,且当x=1时f(x)取最大值1.
是定义在R上的奇函数,且当x=1时f(x)取最大值1.
(1)求出a,b,c的值并写出f(x)的解析式;
(2)若x1∈(0,1),xn+1=f(xn),试比较xn+1与xn的大小并加以证明;
(3)若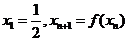 ,求证
,求证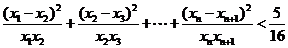 .
.
解:(1)∵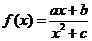 的定义域为R,∴c>0
的定义域为R,∴c>0
又∵f(x)为奇函数,∴f(-x)+f(x)=0
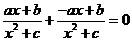 b=0 ……………………………………………………2分
b=0 ……………………………………………………2分
∴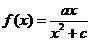 ,又f(1)=1,∴a=1+c>0,∴当x>0时,
,又f(1)=1,∴a=1+c>0,∴当x>0时,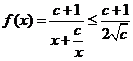
∴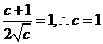 ………………………………………………………………4分
………………………………………………………………4分
∴a=2,b=0,c=1,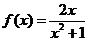 ……………………………………………5分
……………………………………………5分
(2)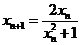 ,∵x1∈(0,1),∴xn+1>0(n∈N*)
,∵x1∈(0,1),∴xn+1>0(n∈N*)
又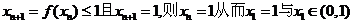 矛盾,∴xn+1<1…7分
矛盾,∴xn+1<1…7分
∴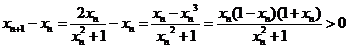 ∴xn+1>xn。…9分
∴xn+1>xn。…9分
(3)∵0<xk<1,
∴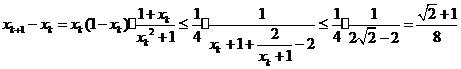
∴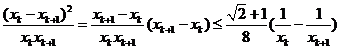 ……………………11分
……………………11分
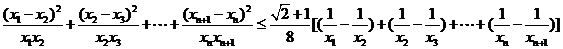
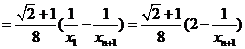
∵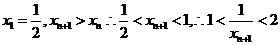
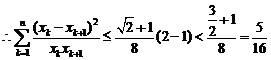 …………………………………14分
…………………………………14分
94、(江苏省盐城市2008届高三六校联考)已知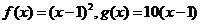 ,数列{an}满足对任意n∈N*有an≠1且a1=2,
,数列{an}满足对任意n∈N*有an≠1且a1=2,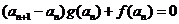
(1)求证:{an-1}是等比数列;
(2)若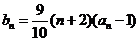 ,当n取何值时,bn取最大值,并求出最大值。
,当n取何值时,bn取最大值,并求出最大值。
解:(1)∵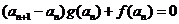
∴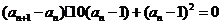 ………………………………3分
………………………………3分
由an≠1知an-1≠0
∴10an+1-10an+an-1=0 ∴10(an+1-1)=9(an-1) ∴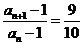
∴{an-1}是以a1-1=1为首项公比为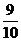 的等比数列
………………7分
的等比数列
………………7分
(2)由(1)知: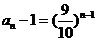
∴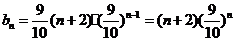 ……………………………9分
……………………………9分
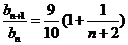 ,当n=7时,
,当n=7时,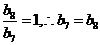
当n<7时,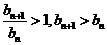 ,当n>7时,
,当n>7时,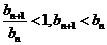 ………12分
………12分
∴当n=7或8时,bn取最大值为b7=b8=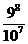 …………………………14分
…………………………14分
93、(江苏省南通通州市2008届高三年级第二次统一测试)第一行是等差数列0,1,2,3,…,2008,将其相邻两项的和依次写下作为第二行,第二行相邻两项的和依次写下作为第三行,依此类推,共写出2008行.
0,1,2,3,…,2005,2006,2007,2008
1,3,5, …, 4011, 4013, 4015
4,8, …, 8024, 8028
……
(1)由等差数列性质知,以上数表的每一行都是等差数列。记各行的公差组成数列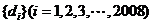 .求通项公式
.求通项公式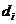 ;
;
(2)各行的第一个数组成数列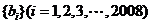 ,求数列
,求数列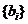 所有各项的和。
所有各项的和。
(1)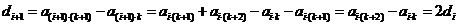 ,
,
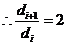 ,则
,则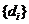 是等比数列,
是等比数列,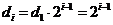 .
6′
.
6′
(2)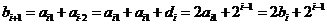 ,
,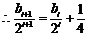 .
.
∴数列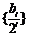 是等差数列,
是等差数列,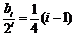 ,所以
,所以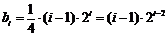 12′
12′
数列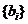 所有各项的和S
所有各项的和S
S=0+1+2×2+3×22+……+2007×22006
用错位相减法,得到S=1003×22008-1 16′
92、(江苏省泰兴市2007-2008学年第一学期高三调研)设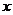 轴、
轴、 轴正方向上的单位向量分别是
轴正方向上的单位向量分别是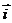 、
、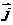 ,坐标平面上点
,坐标平面上点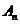 、
、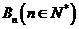 分别满足下列两个条件:①
分别满足下列两个条件:①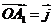 且
且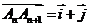 ;②
;②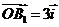 且
且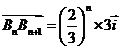 .
.
(1)求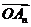 及
及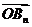 的坐标;
的坐标;
(2)若四边形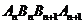 的面积是
的面积是 ,求
,求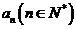 的表达式;
的表达式;
(3)对于(Ⅱ)中的 ,是否存在最小的自然数M,对一切
,是否存在最小的自然数M,对一切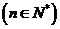 都有
都有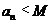 成立?若存在,求M;若不存在,说明理由.
成立?若存在,求M;若不存在,说明理由.
解:(1)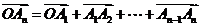
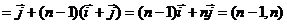
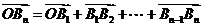
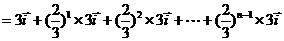
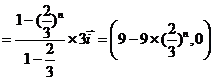 .……………………………………5分
.……………………………………5分
(2)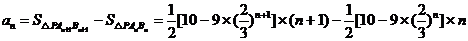
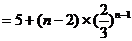 ,……………………………………………………10分
,……………………………………………………10分
(3)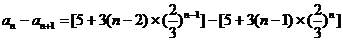
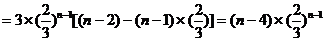
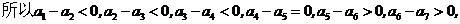 等
等
即在数列 中,
中,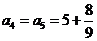 是数列的最大项,所以存在最小的自然数
是数列的最大项,所以存在最小的自然数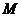
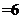 ,对一切
,对一切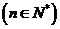 都有
都有 <M成立. …………………………16分
<M成立. …………………………16分
91、(江苏省如东高级中学2008届高三四月份模拟)已知函数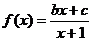 的图象过原点,且关于点
的图象过原点,且关于点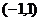 成中心对称.
成中心对称.
(1) 求函数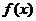 的解析式;
的解析式;
(2) 若数列 满足:
满足: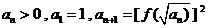 ,求
,求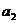 ,
,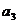 ,
,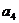 的值,猜想数列
的值,猜想数列 的通项公式
的通项公式 ,并证明你的结论;
,并证明你的结论;
(3) 若数列 的前
的前 项和为
项和为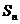 ,判断
,判断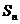 与2的大小关系,并证明你的结论.
与2的大小关系,并证明你的结论.
(1)解:∵函数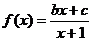 的图象过原点,
的图象过原点,
∴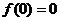 即
即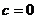 ,
,
∴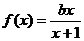 .
.
又函数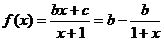 的图象关于点
的图象关于点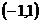 成中心对称,
成中心对称,
∴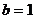 ,
,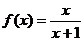 .
.
(2)解:由题意有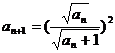 即
即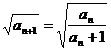 ,
,
即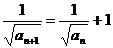 ,即
,即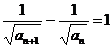 .
.
∴数列{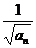 }是以1为首项,1为公差的等差数列.
}是以1为首项,1为公差的等差数列.
∴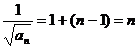 ,即
,即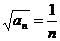 . ∴
. ∴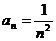 .
.
∴ 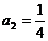 ,
,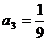 ,
,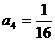 ,
,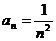 .
.
(3)证明:当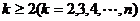 时,
时,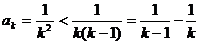
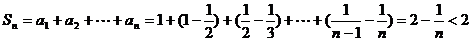
故 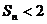
90、(江苏省前黄高级中学2008届高三调研)设数列 满足:
满足: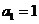 ,且当
,且当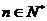 时,
时,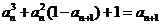
(1) 比较 与
与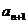 的大小,并证明你的结论;
的大小,并证明你的结论;
(2) 若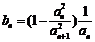 ,其中
,其中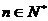 ,证明:
,证明: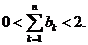
解:(1)由于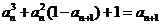 ,则
,则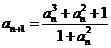 ,
,
∴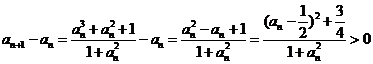 ,∴
,∴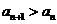
(2)由于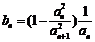 ,由(1)
,由(1)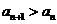 ,则
,则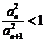 ,
,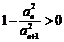 ,
,
而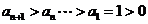 ,则
,则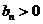 ,∴
,∴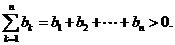
又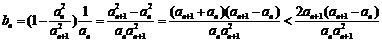
∴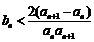 ,
,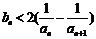
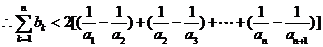
∴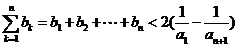 ,而
,而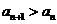 ,且
,且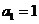 ,故
,故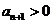
∴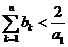 ,因此
,因此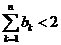 ,从而
,从而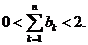
89、(江苏省南通市2008届高三第二次调研考试)已知数列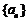 中,
中,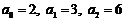 ,且对
,且对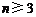 时,有
时,有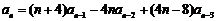 .
.
(Ⅰ)设数列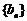 满足
满足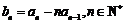 ,证明数列
,证明数列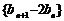 为等比数列,并求数列
为等比数列,并求数列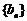 的通项公式;
的通项公式;
(Ⅱ)记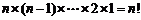 ,求数列
,求数列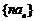 的前n项和Sn.
的前n项和Sn.
(Ⅰ) 证明:由条件,得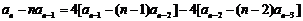 ,
,
则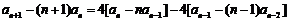 .……………………………………2分
.……………………………………2分
即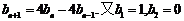 ,所以
,所以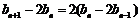 ,
,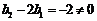 .
.
所以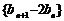 是首项为
是首项为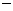 2,公比为2的等比数列. …………………………………4分
2,公比为2的等比数列. …………………………………4分
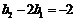 ,所以
,所以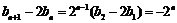 .
.
两边同除以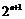 ,可得
,可得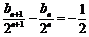 .…………………………………………………6分
.…………………………………………………6分
于是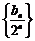 为以
为以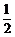 首项,-
首项,-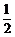 为公差的等差数列.
为公差的等差数列.
所以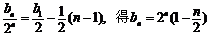 .………………………………………………8分
.………………………………………………8分
(Ⅱ)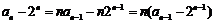 ,令
,令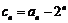 ,则
,则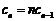 .
.
而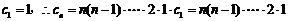 .
.
∴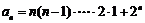 .
……………………………………………………………12分
.
……………………………………………………………12分
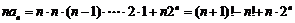 ,
,
∴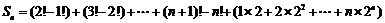 .………………14分
.………………14分
令Tn=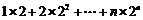 , ①
, ①
则2Tn=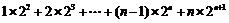 . ②
. ②
①-②,得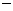 Tn=
Tn=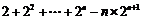 ,Tn=
,Tn=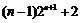 .
.
∴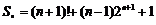 .……………………………………………………………16分
.……………………………………………………………16分
评讲建议:
此题主要考查数列的概念、等差数列、等比数列、数列的递推公式、数列的通项求法、数列前n项和的求法,作新数列法,错项相消法,裂项法等知识与方法,同时考查学生的分析问题与解决问题的能力,逻辑推理能力及运算能力.讲评时着重在正确审题,怎样将复杂的问题化成简单的问题,本题主要将一个综合的问题分解成几个常见的简单问题.事实上本题包含了好几个常见的数列题.本题还有一些另外的解法,如第一问的证明还可以直接代.
88、(江苏省南京市2008届高三第一次调研测试)用数学归纳法证明:当n是不小于5的自然数时,总有2n > n2成立.
证明:(1)当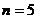 时,
时,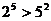 ,结论成立.
,结论成立.
(2)假设当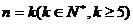 时,结论成立,即:
时,结论成立,即: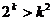
那么当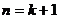 时,左边=
时,左边=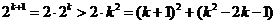
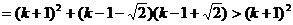 =右边.
=右边.
 也就是说,当
也就是说,当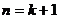 时,结论成立.…………………………6分.
时,结论成立.…………………………6分.
 由(1)、(2)可知,不等式
由(1)、(2)可知,不等式 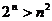 对
对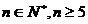 时恒成立.……8分.
时恒成立.……8分.
87、(江苏省南京市2008届高三第一次调研测试)设数列{an},{bn}都是等差数列,它们的前n项的和分别为Sn , Tn ,若对一切n ∈ N*,都有Sn+3 = Tn .
(1)若a1 ≠ b1,试分别写出一个符号条件的数列{an}和{bn};
(2)若a1 + b1 = 1,数列{cn}满足:cn = 4 an + l(–1)n–12 bn,且当n ∈ N*时,cn+1 ≥ cn恒成立,求实数l的最大值.
解:(1)答案不唯一,例如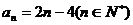 ,
,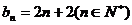 ……4分
……4分
(2)设数列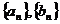 的公差分别是
的公差分别是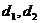 ,
,
则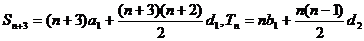
 对一切
对一切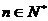 ,有
,有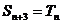 ,
,

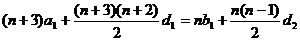 ……………………6分
……………………6分
即: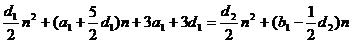
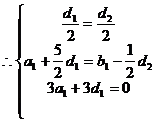 即
即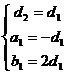 …………………………………8分
…………………………………8分
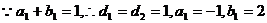
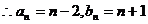 ………………………………………………10分
………………………………………………10分
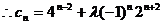
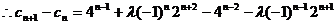
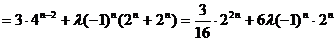
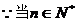 时,
时,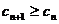 恒成立,
恒成立,
即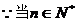 时,
时,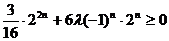 恒成立
恒成立
 当
当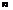 为正奇数时,
为正奇数时,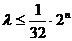 恒成立,而
恒成立,而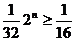 ,
,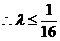 ;
;
当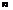 为正偶数时,
为正偶数时,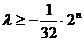 恒成立,而
恒成立,而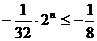 ,
,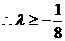
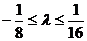
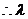 的最大值是
的最大值是 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com