
2.把下列对数式写成指数式
(1) 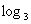 9=2 ⑵
9=2 ⑵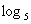 125=3 ⑶
125=3 ⑶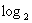
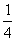 =-2 ⑷
=-2 ⑷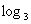
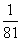 =-4
=-4
解:(1)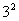 =9 (2)
=9 (2)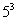 =125 (3)
=125 (3)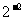 =
=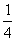 (4)
(4)  =
=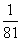
1.把下列指数式写成对数式
(1) 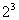 =8; (2)
=8; (2)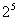 =32 ; (3)
=32 ; (3)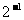 =
=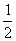 ; (4)
; (4)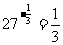 .
.
解:(1)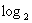 8=3 (2)
8=3 (2) 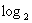 32=5 (3)
32=5 (3) 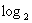
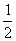 =-1 (4)
=-1 (4) 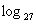
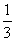 =-
=-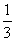
例1.将下列指数式写成对数式:
(1)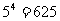 (2)
(2)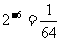 (3)
(3)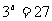 (4)
(4) 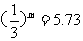
解:(1)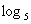 625=4; (2)
625=4; (2)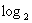
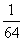 =-6; (3)
=-6; (3)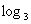 27=a; (4)
27=a; (4)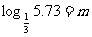 .
.
例2. 将下列对数式写成指数式:
(1)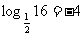 ; (2)
; (2)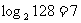 ; (3)
; (3)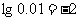 ; (4)
; (4)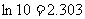 .
.
解:(1)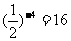 (2)
(2)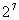 =128; (3)
=128; (3) =0.01; (4)
=0.01; (4)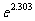 =10.
=10.
例3.求下列各式中的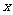 的值:
的值:
(1)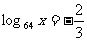 ; (2)
; (2)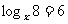 (3)
(3)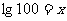 (4)
(4)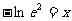
例4.计算: ⑴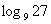 ,⑵
,⑵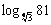 ,⑶
,⑶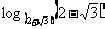 ,⑷
,⑷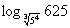 .
.
解法一:⑴设 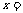
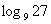 则
则 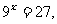
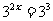 , ∴
, ∴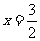
⑵设 
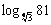 则
则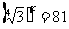 ,
, 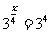 , ∴
, ∴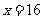
⑶令 
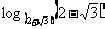 =
=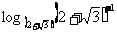 , ∴
, ∴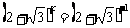 , ∴
, ∴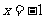
⑷令 
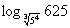 , ∴
, ∴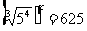 ,
, 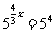 , ∴
, ∴
解法二:
⑴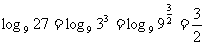 ; ⑵
; ⑵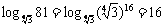
⑶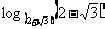 =
=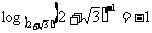 ;⑷
;⑷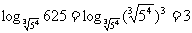
定义:一般地,如果 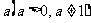 的b次幂等于N,就是
的b次幂等于N,就是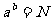 ,那么数 b叫做以a为底 N的对数,记作
,那么数 b叫做以a为底 N的对数,记作 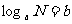 ,a叫做对数的底数,N叫做真数.
,a叫做对数的底数,N叫做真数.
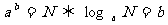
例如: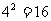

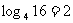 ;
; 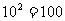

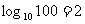 ;
;
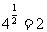

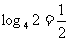 ;
; 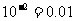

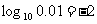 .
.
探究:1。是不是所有的实数都有对数?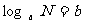 中的N可以取哪些值?
中的N可以取哪些值?
⑴ 负数与零没有对数(∵在指数式中 N > 0 )
2.根据对数的定义以及对数与指数的关系,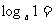 ?
? 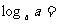 ?
?
⑵ 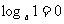 ,
,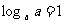 ;
;
∵对任意  且
且 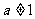 , 都有
, 都有 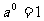 ∴
∴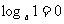 同样易知:
同样易知: 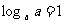
⑶对数恒等式
如果把 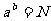 中的 b写成
中的 b写成 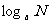 , 则有
, 则有  .
.
⑷常用对数:我们通常将以10为底的对数叫做常用对数.为了简便,N的常用对数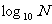 简记作lgN.
简记作lgN.
例如: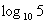 简记作lg5;
简记作lg5; 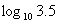 简记作lg3.5.
简记作lg3.5.
⑸自然对数:在科学技术中常常使用以无理数e=2.71828……为底的对数,以e为底的对数叫自然对数,为了简便,N的自然对数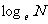 简记作lnN.
简记作lnN.
例如: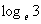 简记作ln3;
简记作ln3; 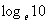 简记作ln10.
简记作ln10.
(6)底数的取值范围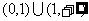 ;真数的取值范围
;真数的取值范围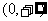 .
.
假设2002年我国国民生产总值为a亿元,如果每年平均增长8%,那么经过多少年国民生产总值是2002年的2倍?
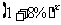 =2
=2 x=?
x=?
也是已知底数和幂的值,求指数.你能看得出来吗?怎样求呢?
《习案》作业十八。
思考:作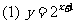 ;
; 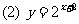 ;的图象
;的图象
2. 求指数复合函数定义域、值域.
1. 运用指数函数单调性比较大小;
(四)已知: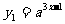 ,
,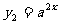 (a﹥0,a≠1),
(a﹥0,a≠1),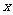 为何值时,
为何值时,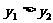 ?
?
(三)解不等式:(1) (2)
(2)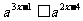 (a﹥0,a≠1)
(a﹥0,a≠1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com