
68、(湖北省三校联合体高2008届2月测试)已知数列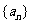 的首项
的首项 ,前
,前 项和为
项和为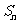 ,且
,且 、
、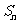 、
、 分别是直线
分别是直线 上的点A、B、C的横坐标,点B分
上的点A、B、C的横坐标,点B分 所成的比为
所成的比为 ,设
,设
 。
。
⑴ 判断数列 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
⑵ 设 ,证明:
,证明: 。
。
⑴由题意得 ……………3分
……………3分


 数列
数列 是以
是以 为首项,以2为公比的等比数列。………………6分
为首项,以2为公比的等比数列。………………6分
[则

 (
(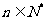 )]
)]
⑵由 及
及 得
得

 ,……………………………………………………………8分
,……………………………………………………………8分
则
 ……………………10分
……………………10分

 ………………12分
………………12分
67、(湖北省八校高2008第二次联考)已知数列 ,
, 满足
满足 ,数列
,数列 的前
的前 项和为
项和为 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求证: ;
;
(Ⅲ)求证:当 时,
时, .
.
解:(1)由 ,得
,得 ,代入
,代入 ,得
,得 ,
,
整理,得 ,从而有
,从而有 ,
, ,
,
 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列, 即
即 . …………………(4分)
. …………………(4分)
(2) ,
,  ,
,
 ,
,
 ,
,

 .
…………………(8分)
.
…………………(8分)
(3) ,
,

 .
.
由(2)知 ,
, ,
,




 .
.
…………………(14分)
66、(黑龙江省哈师大附中2008届高三上期末)已知数列{an}满足a1=5,a2=5,an+1=an+6an-1(n≥2且n∈N*)
(1)求出所有使数列 值,并说明理由;
值,并说明理由;
(2)求数列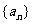 的通项公式;
的通项公式;
(3)求证:
解:(1)
(2)
(3)当 时,
时,

65、(黑龙江省哈师大附中2008届高三上期末)已知二次函数f(x)=ax2+bx+c的图象顶点坐标是(,-),且f(3)=2
(1)求y=f(x)的表达式,并求出f(1),f(2)的值;
(2)数列 ,若对任意的实数
,若对任意的实数 ,其中
,其中 是定义在实数集R上的一个函数,求数列
是定义在实数集R上的一个函数,求数列 的通项公式;
的通项公式;
(3)设圆 是各项都是正数的等比数列,设
是各项都是正数的等比数列,设 个圆的面积之和,求
个圆的面积之和,求
解:(1)

(2)令

(3)


64、(黑龙江省哈师大附中2008届高三上期末)已知数列{an}的前n项和为Sn,并且满足a1=2,nan+1=Sn+n(n+1).
(1)求数列 ;
;
(2)设
解:(1)

(2)

63、(本题满分12分)(黑龙江省哈尔滨三中2008年高三上期末)已知 ,数列
,数列

(1)证明:
(2)证明:
(3)设 的前n项和,判断
的前n项和,判断 的大小,并说明理由。
的大小,并说明理由。
答案:(1)略
(2)略
(3)
62、(黑龙江省哈尔滨三中2008年高三上期末)已知二次函数 的图象过点(-4n,0)且
的图象过点(-4n,0)且
(1)求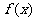 的解析式;
的解析式;
(2)若数列 的通项公式;
的通项公式;
(3)对于(2)中的数列
答案:(1)
(2)
(3)略
61、(黑龙江省哈尔滨九中2008年第三次模拟考试)已知 数列
数列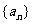 的前n项和为
的前n项和为 ,点
,点 在曲线
在曲线 上
上 且
且 .
.
(1)求数列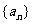 的通项公式;
的通项公式;
(2)数列 的前n项和为且
的前n项和为且 满足
满足 ,设定
,设定 的值使得数列
的值使得数列 是等差数列;
是等差数列;
(3)求证: .
.
解:(1)
∴
∴
∴数列 是等差数列,首项
是等差数列,首项 公差d=4
公差d=4
∴
∴
∵
∴ …………(4分)
…………(4分)
(2)由
得
∴
∴
∴
若 为等差数列,则
为等差数列,则
∴
(3)
∴

∴

 ……………………12分
……………………12分
60、已知数列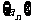 中
中 ,其前n项和为 满足
,其前n项和为 满足 .
.
(1)试求数列 的通项公式.
的通项公式.
(2)令
 是数列
是数列 的前n项和,证明:
的前n项和,证明: .
.
(3)证明:对任意的 ,均存在
,均存在 ,使得(2)中的
,使得(2)中的 成立.
成立.
解:(1)由 得
得
 ,
, ,即
,即
又 ,
,


故数列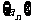 的通项公式为
的通项公式为 .……………………(4分)
.……………………(4分)
(2)

 ……………………(8分)
……………………(8分)
(3)证明:由(2)可知
若 ,则得
,则得 ,化简得
,化简得
 ,
,
当 ,即
,即 ………………(10分)
………………(10分)
当 ,即
,即
 ,取
,取 即可,
即可,
综上可知,对任意的 均存在
均存在 使得时(2)中的
使得时(2)中的 成立(12分)
成立(12分)
59、(河南省开封市2008届高三年级第一次质量检)函数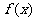 对任意x∈R都有f(x)+f(1-x)=.
对任意x∈R都有f(x)+f(1-x)=.
(1)求 的值;
的值;
(2)数列 的通项公式。
的通项公式。
(3)令 试比较Tn与Sn的大小。
试比较Tn与Sn的大小。
解:(1)令
令
(2)
又 ,两式相加
,两式相加



 是等差数列
是等差数列
(3)






湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com