
32、(广东省佛山市2008年高三教学质量检测一)抛物线 的准线的方程为
的准线的方程为 ,该抛物线上的每个点到准线
,该抛物线上的每个点到准线 的距离都与到定点N的距离相等,圆N是以N为圆心,同时与直线
的距离都与到定点N的距离相等,圆N是以N为圆心,同时与直线 相切的圆,
相切的圆,
(Ⅰ)求定点N的坐标;
(Ⅱ)是否存在一条直线 同时满足下列条件:
同时满足下列条件:
①  分别与直线
分别与直线 交于A、B两点,且AB中点为
交于A、B两点,且AB中点为 ;
;
②  被圆N截得的弦长为
被圆N截得的弦长为 .
.
解:(1)因为抛物线 的准线的方程为
的准线的方程为
所以 ,根据抛物线的定义可知点N是抛物线的焦点,
-----------2分
,根据抛物线的定义可知点N是抛物线的焦点,
-----------2分
所以定点N的坐标为 ----------------------------3分
----------------------------3分
(2)假设存在直线 满足两个条件,显然
满足两个条件,显然 斜率存在,
-----------4分
斜率存在,
-----------4分
设 的方程为
的方程为 ,
, ------------------------5分
------------------------5分
以N为圆心,同时与直线 相切的圆N的半径为
相切的圆N的半径为 , ----6分
, ----6分
方法1:因为 被圆N截得的弦长为2,所以圆心到直线的距离等于1, -------7分
被圆N截得的弦长为2,所以圆心到直线的距离等于1, -------7分
即 ,解得
,解得 ,
-------------------------------8分
,
-------------------------------8分
当 时,显然不合AB中点为
时,显然不合AB中点为 的条件,矛盾!
--------------9分
的条件,矛盾!
--------------9分
当 时,
时, 的方程为
的方程为 ----------------------------10分
----------------------------10分
由 ,解得点A坐标为
,解得点A坐标为 ,
------------------11分
,
------------------11分
由 ,解得点B坐标为
,解得点B坐标为 ,
------------------12分
,
------------------12分
显然AB中点不是 ,矛盾!
----------------------------------13分
,矛盾!
----------------------------------13分
所以不存在满足条件的直线 .
------------------------------------14分
.
------------------------------------14分
方法2:由 ,解得点A坐标为
,解得点A坐标为 ,
------7分
,
------7分
由 ,解得点B坐标为
,解得点B坐标为 ,
------------8分
,
------------8分
因为AB中点为 ,所以
,所以 ,解得
,解得 ,
---------10分
,
---------10分
所以 的方程为
的方程为 ,
,
圆心N到直线 的距离
的距离 ,
-------------------------------11分
,
-------------------------------11分
因为 被圆N截得的弦长为2,所以圆心到直线的距离等于1,矛盾! ----13分
被圆N截得的弦长为2,所以圆心到直线的距离等于1,矛盾! ----13分
所以不存在满足条件的直线 .
-------------------------------------14分
.
-------------------------------------14分
方法3:假设A点的坐标为 ,
,
因为AB中点为 ,所以B点的坐标为
,所以B点的坐标为 ,
-------------8分
,
-------------8分
又点B 在直线 上,所以
上,所以 ,
----------------------------9分
,
----------------------------9分
所以A点的坐标为 ,直线
,直线 的斜率为4,
的斜率为4,
所以 的方程为
的方程为 ,
-----------------------------10分
,
-----------------------------10分
圆心N到直线 的距离
的距离 ,
-----------------------------11分
,
-----------------------------11分
因为 被圆N截得的弦长为2,所以圆心到直线的距离等于1,矛盾! ---------13分
被圆N截得的弦长为2,所以圆心到直线的距离等于1,矛盾! ---------13分
所以不存在满足条件的直线 .
.
31、(甘肃省兰州一中2008届高三上期期末考试)已知椭圆C: 的左、右焦点为F1、F2,离心率为e.
直线
的左、右焦点为F1、F2,离心率为e.
直线 与x轴、y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
与x轴、y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
(Ⅰ)证明: ;
;
(Ⅱ)若 的周长为6;写出椭圆C的方程.
的周长为6;写出椭圆C的方程.
解:(Ⅰ)证法一:因为A、B分别是直线 轴、y轴的交点,
轴、y轴的交点,
所以A、B的坐标分别是 …………2分
…………2分
由 …………4分
…………4分
所以点M的坐标是
即  ………………6分
………………6分
证法二:因为A、B分别是直线 轴、y轴的交点,所以A、B的坐标分别是
轴、y轴的交点,所以A、B的坐标分别是 ………………2分
………………2分
设M的坐标是
 ………………4分
………………4分
因为点M在椭圆上,所以 
即 
 …………6分
…………6分
(Ⅱ)当 的周长为6,得
的周长为6,得
所以
30、(甘肃省河西五市2008年高三第一次联考)已知双曲线 的离心率e=2,且
的离心率e=2,且 、
、 分别是双曲线虚轴的上、下端点
分别是双曲线虚轴的上、下端点
(Ⅰ)若双曲线过点 (
( ,
, ),求双曲线的方程;
),求双曲线的方程;
(Ⅱ)在(Ⅰ)的条件下,若 、
、 是双曲线上不同的两点,且
是双曲线上不同的两点,且 ,求直线
,求直线 的方程
的方程
解:(Ⅰ)∵双曲线方程为 
∴ ,
,
∴双曲线方程为  ,又曲线C过点Q(2,
,又曲线C过点Q(2, ),
),
∴
∴双曲线方程为  ………………5分
………………5分
(Ⅱ)∵ ,∴M、B2、N三点共线
,∴M、B2、N三点共线
∵ ,
∴
,
∴
(1)当直线 垂直x轴时,不合题意
垂直x轴时,不合题意
(2)当直线 不垂直x轴时,由B1(0,3),B2(0,-3),
不垂直x轴时,由B1(0,3),B2(0,-3),
可设直线 的方程为
的方程为 ,①
,①
∴直线 的方程为
的方程为  ②
②
由①,②知  代入双曲线方程得
代入双曲线方程得
 ,得
,得 ,
,
解得  , ∴
, ∴ ,
,
故直线 的方程为
的方程为 
29、(福建省漳州一中2008年上期期末考试)已知 ,点
,点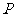 满足
满足 ,记点
,记点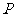 的轨迹为
的轨迹为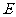 .
.
(Ⅰ)求轨迹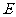 的方程;
的方程;
(Ⅱ)若直线 过点
过点 且与轨迹
且与轨迹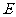 交于
交于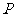 、
、 两点.
两点.
(i)设点 ,问:是否存在实数
,问:是否存在实数 ,使得直线
,使得直线 绕点
绕点 无论怎样转动,都有
无论怎样转动,都有 成立?若存在,求出实数
成立?若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(ii)过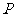 、
、 作直线
作直线 的垂线
的垂线 、
、 ,垂足分别为
,垂足分别为 、
、 ,记
,记 ,求
,求 的取值范围.
的取值范围.
解:(Ⅰ)由
 知,点
知,点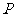 的轨迹
的轨迹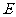 是以
是以 、
、 为焦点的双曲线右支,由
为焦点的双曲线右支,由 ,∴
,∴ ,故轨迹E的方程为
,故轨迹E的方程为 …(3分)
…(3分)
(Ⅱ)当直线l的斜率存在时,设直线l方程为 ,与双曲线方程联立消
,与双曲线方程联立消 得
得 ,设
,设 、
、 ,
,
 ∴
∴ , 解得
, 解得 ………………………………………(5分)
………………………………………(5分)
(i)∵

 ……………………(7分)
……………………(7分)
假设存在实数 ,使得
,使得 ,
,
故得 对任意的
对任意的 恒成立,
恒成立,
∴ ,解得
,解得
∴当 时,
时, .
.
当直线l的斜率不存在时,由 及
及 知结论也成立,
知结论也成立,
综上,存在 ,使得
,使得 . …………………………………………(8分)
. …………………………………………(8分)
(ii)∵ ,∴直线
,∴直线 是双曲线的右准线,…………………………(9分)
是双曲线的右准线,…………………………(9分)
由双曲线定义得: ,
, ,
,
方法一:∴

 …………………………………………(10分)
…………………………………………(10分)
∵ ,∴
,∴ ,∴
,∴ ………………………………………(11分)
………………………………………(11分)
注意到直线的斜率不存在时, ,
,
 综上,
综上, ………………………………………………………………(12分)
………………………………………………………………(12分)
方法二:设直线 的倾斜角为
的倾斜角为 ,由于直线
,由于直线
与双曲线右支有二个交点,∴ ,过
,过
作 ,垂足为
,垂足为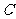 ,则
,则 ,
,
∴

……………………………………………………(10分)
由 ,得
,得
故:
28、(福建省仙游一中2008届高三第二次高考模拟测试)已知方向向量为 的直线
的直线 过椭圆C:=1(a>b>0)的焦点以及点(0,
过椭圆C:=1(a>b>0)的焦点以及点(0, ),椭圆C的中心关于直线
),椭圆C的中心关于直线 的对称点在椭圆C的右准线上。
的对称点在椭圆C的右准线上。
⑴求椭圆C的方程。
⑵过点E(-2,0)的直线 交椭圆C于点M、N,且满足
交椭圆C于点M、N,且满足 ,(O为坐标原点),求直线
,(O为坐标原点),求直线 的方程。
的方程。
解:⑴直线 ①,过原点垂直于
①,过原点垂直于 的直线方程为
的直线方程为 ②
②
解①②得 ,∵椭圆中心O(0,0)关于直线
,∵椭圆中心O(0,0)关于直线 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
∴ ,
…………………(2分)
,
…………………(2分)
∵直线 过椭圆焦点,∴该焦点坐标为(2,0),∴
过椭圆焦点,∴该焦点坐标为(2,0),∴ ,
,
故椭圆C的方程为 ③…………………(4分)
③…………………(4分)
⑵当直线 的斜率存在时,设
的斜率存在时,设 ,代入③并整理得
,代入③并整理得
 ,设
,设 ,
,
则 ……………(5分)
……………(5分)
∴ ,……(7分)
,……(7分)
点 到直线
到直线 的距离
的距离 .
.
∵ ,即
,即 ,
,
又由 得
得  ,
,
∴ ,…………………………(9分)
,…………………………(9分)
而 ,∴
,∴ ,即
,即 ,
,
解得 ,此时
,此时 …………………………………(11分)
…………………………………(11分)
当直线 的斜率不存在时,
的斜率不存在时, ,也有
,也有 ,
,
经检验,上述直线 均满足
均满足 ,
,
故直线 的方程为
的方程为 
27、(福建省厦门市2008学年高三质量检查)已知曲线C上任意一点M到点F(0,1)的距离比它到直线 的距离小1。
的距离小1。
(1)求曲线C的方程;
(2)过点
①当 的方程;
的方程;
②当△AOB的面积为 时(O为坐标原点),求
时(O为坐标原点),求 的值。
的值。
(1)解法一:设 , …………1分
, …………1分
即
当 ; …………3分
; …………3分
当 …………4分
…………4分
化简得 不合
不合
故点M的轨迹C的方程是 …………5分
…………5分
(1)解法二: 的距离小于1,
的距离小于1,
∴点M在直线l的上方,
点M到F(1,0)的距离与它到直线 的距离相等 …………3分
的距离相等 …………3分

所以曲线C的方程为 …………5分
…………5分
(2)当直线m的斜率不存在时,它与曲线C只有一个交点,不合题意,
设直线m的方程为 ,
,
代入 (☆) …………6分
(☆) …………6分
 与曲线C恒有两个不同的交点
与曲线C恒有两个不同的交点
设交点A,B的坐标分别为 ,
,
则 …………7分
…………7分
①由 ,
,
 …………9分
…………9分
②
点O到直线m的距离 ,
,
 …………10分
…………10分
 ,
,
 (舍去)
(舍去)
 …………12分
…………12分
当 方程(☆)的解为
方程(☆)的解为
若
若 …………13分
…………13分
当 方程(☆)的解为
方程(☆)的解为
若
若 …………14分
…………14分
所以,
26、(福建省泉州一中高2008届第一次模拟检测)已知椭圆C: +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
(1)求直线ON(O为坐标原点)的斜率KON ;
(2)对于椭圆C上任意一点M ,试证:总存在角 (
( ∈R)使等式:
∈R)使等式: =cos
=cos
 +sin
+sin
 成立。
成立。
解:(1)设椭圆的焦距为2c,因为 ,所以有
,所以有 ,故有
,故有 。从而椭圆C的方程可化为:
。从而椭圆C的方程可化为: ①
………2分
①
………2分
易知右焦点F的坐标为( ),
),
据题意有AB所在的直线方程为: ②
………3分
②
………3分
由①,②有: ③
③
设 ,弦AB的中点
,弦AB的中点 ,由③及韦达定理有:
,由③及韦达定理有:

所以 ,即为所求。
………5分
,即为所求。
………5分
(2)显然 与
与 可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量
可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量 ,有且只有一对实数
,有且只有一对实数 ,使得等式
,使得等式 成立。设
成立。设 ,由1)中各点的坐标有:
,由1)中各点的坐标有:
 ,所以
,所以
 。 ………7分
。 ………7分
又点在椭圆C上,所以有 整理为
整理为 。
④
。
④
由③有: 。所以
。所以
 ⑤
⑤
又A﹑B在椭圆上,故有 ⑥
⑥
将⑤,⑥代入④可得: 。
………11分
。
………11分
对于椭圆上的每一个点 ,总存在一对实数,使等式
,总存在一对实数,使等式 成立,而
成立,而
在直角坐标系 中,取点P(
中,取点P( ),设以x轴正半轴为始边,以射线OP为终边的角为
),设以x轴正半轴为始边,以射线OP为终边的角为 ,显然
,显然
 。
。
也就是:对于椭圆C上任意一点M ,总存在角 (
( ∈R)使等式:
∈R)使等式: =cos
=cos
 +sin
+sin
 成立。
成立。
50、(上海市部分重点中学2008届高三第二次联考)已知AB是椭圆 的长轴,若把该长轴
的长轴,若把该长轴 等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点
等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点 ,设左焦点为
,设左焦点为 ,则
,则
答案:A
49、(山西大学附中2008届二月月考)点P是双曲线 的一个交点,且2∠PF1F2=∠PF2F1,其中F1、F2是双曲线C1的两个焦点,则双曲线C1的离心率为
.
的一个交点,且2∠PF1F2=∠PF2F1,其中F1、F2是双曲线C1的两个焦点,则双曲线C1的离心率为
.
答案:+1
48、(山东省郓城一中2007-2008学年第一学期期末考试)已知F1、F2是椭圆 =1(5<a<10=的两个焦点,B是短轴的一个端点,则△F1BF2的面积的最大值是
=1(5<a<10=的两个焦点,B是短轴的一个端点,则△F1BF2的面积的最大值是
答案:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com