
翰林汇6、x1=x2=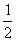 翰林汇7、65.5 翰林汇8、y=-x+2
翰林汇9、70° 翰林汇10、1cm,15cm
翰林汇7、65.5 翰林汇8、y=-x+2
翰林汇9、70° 翰林汇10、1cm,15cm
翰林汇二、1、 B 翰林汇2、 C 翰林汇 3、 B 翰林汇 4、 B 翰林汇 5、 A 翰林汇
26、提示:过点A作AG⊥x轴,过点B作BH⊥x轴,(1)解析式: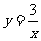
(2)求得:k2=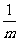 ; b=
; b= 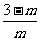
五:23、作DF∥AC交BE于F。证△ACE≌△FED可得EC=ED。
24、(1)证△=2k2+8>0 (2)k=±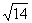 。
。
六:25、连结OD,证△PDO∽△PEC得PD·PC=PO·PE,
由切割线定理得PA·PB=PD·PC,∴PA·PB=PO·PE。
20、(1)A(0,1);(2)b=1,k=-2。
7、300;8、DE=BF;9、6;10、6.5。
=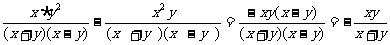 , ∵
, ∵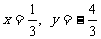 ,∴原式=
,∴原式=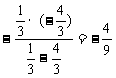 。 3.解:∵BF=CF·ctg300=
。 3.解:∵BF=CF·ctg300=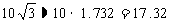 ,AE=2DE=20,∴AB=17.32+3+20≈40.3 (米)。 4.BD=
,AE=2DE=20,∴AB=17.32+3+20≈40.3 (米)。 4.BD=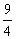 , 5.解:∵∠B=900,∠A=300,BC=3,∴AC=2BC=6,设⊙O半径为R,AB切⊙O于D,则AO=6-R,△ADO∽△ABC,∴
, 5.解:∵∠B=900,∠A=300,BC=3,∴AC=2BC=6,设⊙O半径为R,AB切⊙O于D,则AO=6-R,△ADO∽△ABC,∴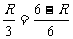 ,解得:R=2。 四、1.X1=2,X2=-1(舍去)。 2.解:(1)由题意知:AB+BC=k-2, AB·BC=2k, 3AB=2BC,解得:k=12,(k=
,解得:R=2。 四、1.X1=2,X2=-1(舍去)。 2.解:(1)由题意知:AB+BC=k-2, AB·BC=2k, 3AB=2BC,解得:k=12,(k=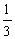 舍去),AB=4,BC=6,(2)当点M离开点B是4时,△AED面积是△DEM面积的3倍,证明如下:∵S△AED=3S△DEM,∴AE=3EM,∴AM=4EM,设EM为x,则AE=3,AM=4 x,∵ABCD是矩形,∴∠B=900,AD∥BC,∴∠DAE=∠BMA,∵DE⊥AM,∴∠AED=∠B,∴△ADE∽△MAB,
舍去),AB=4,BC=6,(2)当点M离开点B是4时,△AED面积是△DEM面积的3倍,证明如下:∵S△AED=3S△DEM,∴AE=3EM,∴AM=4EM,设EM为x,则AE=3,AM=4 x,∵ABCD是矩形,∴∠B=900,AD∥BC,∴∠DAE=∠BMA,∵DE⊥AM,∴∠AED=∠B,∴△ADE∽△MAB,
∴3x∶BM=6∶4x,∴BM=2 x2,∵AB2+BM2=AM2,∴42+(2x2)2=(4x)2,解得:x2=2,∴BM=2×2=4, 3.解:设货车每小时走x千米,根据题意得: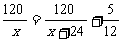 ,解得:X1=72,X2=-96 (舍去)。当X=72时,x+24=96,∴货车每小时走72千米,客车每小时走96千米。 4.解:(1)由抛物线的顶点为B(-1,m)得:
,解得:X1=72,X2=-96 (舍去)。当X=72时,x+24=96,∴货车每小时走72千米,客车每小时走96千米。 4.解:(1)由抛物线的顶点为B(-1,m)得: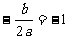 ,所以, b=2a,① 因为抛物线经过点A(1,0)、B(-1,m),所以,a+b+c=0 ② ,a-b+c=m ③。由①②③组成的方程组解得:
,所以, b=2a,① 因为抛物线经过点A(1,0)、B(-1,m),所以,a+b+c=0 ② ,a-b+c=m ③。由①②③组成的方程组解得: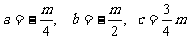 ,所以此抛物线的解析式为
,所以此抛物线的解析式为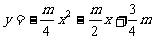 (2)
(2) ; (3)∵∠AOC是直角,△AOC为等腰三角形,∴OC=OA=1,∴点C的坐标为(0,1)或(0,-1),把C(0,1)代入
; (3)∵∠AOC是直角,△AOC为等腰三角形,∴OC=OA=1,∴点C的坐标为(0,1)或(0,-1),把C(0,1)代入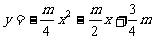 ,解得:
,解得: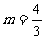 ,又把C(0,-1)代入
,又把C(0,-1)代入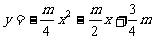 ,解得:
,解得: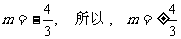 。 5.(1)证明:∵∠POC=∠PCE,∠OPC=∠CPE,∴∠OCP=∠CEP,∵CD⊥AB,∴∠CEP=900,∴∠OCP=900,∴PC是⊙O的切线; (2)解:设OE=x ,∵OE∶EA=1∶2,∴EA=2x,OA=OC=3x,OP=3x+6,∵CE是高,∴OC2=OE·OP,即(3x)2=x(3x+6),∴x=1,OA=3。
。 5.(1)证明:∵∠POC=∠PCE,∠OPC=∠CPE,∴∠OCP=∠CEP,∵CD⊥AB,∴∠CEP=900,∴∠OCP=900,∴PC是⊙O的切线; (2)解:设OE=x ,∵OE∶EA=1∶2,∴EA=2x,OA=OC=3x,OP=3x+6,∵CE是高,∴OC2=OE·OP,即(3x)2=x(3x+6),∴x=1,OA=3。
5、、(1)k=3;(2) C的横坐标是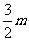 。(3)m=
。(3)m=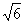 。4、(1)y=-3x2 +252x-4860。(2)y的最大值是432。5、k=-1。
。4、(1)y=-3x2 +252x-4860。(2)y的最大值是432。5、k=-1。
4、(1)证AB=AC可得△ABE≌△ACD。(2)证△BCE∽△ACB可求得AE=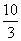
3、作OH⊥AD于H,证AB·AC=EN·BN,从而得AE2 =BN·EN
2、(1)(略)。(2)过A作AM⊥BC交BC于M。设法求得AM=4,即可求得DE=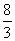 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com