1、连结CR，QR，连结PC，并延长。只要证CR∥OQ可得结论。

3、(1)①DE是⊙O的切线。②AB=BC ③∠A=∠C ④DE²=BE·CE (或⑤CD²=CE·CB

⑥ ∠C+∠CDE=90°⑦CE² +DE² =CD² )。　　　

(2)①CE=BE。②DE=BE。③ DE=CE。④DE∥AB。⑤CB是⊙O的切线。⑥DE=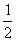AB。

⑦∠A=∠CDE= 45°。⑧CB²=CD·CA等等。4、(1)证∠BAD=∠EDC可得ΔABD∽ΔDCE。

(2)y=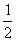x² 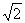－ x+2。(0＜x＜2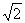。(3) ①当AD=AE时不成立；②当AE=DE时,求得AE=1 ③当AD=DE时,求得AE=4－2。

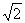2、　 (1)连结BO，证∠FEB=∠ABC，可得EF∥GC。(2)连结BF、FD，证ΔADE∽ΔABF得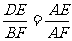，从EF∥GC和证BF=DF可得证结论。。

1、　 AB=69.5

1、(1)只要证∠EBM+∠BEM=90°, ∠BEM+∠ECB=90°∴∠EBM=∠ECB.　　 (2) 只要先证ΔABF≌ΔBCE。 2、CD=120米，受影响，1/150小时=24秒。3、BD=12，CD=6，S=36cm² . 4、(1) 只要先证ΔABE∽ΔCDA。(2)具备条件BF=AD(或FA//BD或∠BCF=∠DCA等)。

2．EC=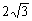。3．解：∵⊙O截△ABC三边所得的三条弦相等，∴点O到△ABC三边相等，即点O为△ABC的内心，∴∠OBC+∠OCB=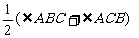，∵∠BOC=128⁰，∴∠OBC+∠OCB=52⁰，∴=104⁰，∴∠A=180⁰－104⁰=76⁰。　 二、证明题：1．证明：连结AB，∵∠BAC=∠F，∠BAC+∠E=180⁰，∴∠E+∠F=180⁰，∴CE∥DF。　 2．证明：连结BE，∵AD平分∠MAC，∴∠MAD=∠CAD，∵∠MAD=∠EAB，∴∠CAD=∠EAB，∵∠ACD=∠AEB，∴△ACD∽△AEB，∴AD∶AB=AC∶AE，即 AD·AE=AB·AC，∵AD·DE=DB·DC，∴AD(AD+AE)=DB·DC，∴AD²=DB·DC－AD·AE，∵AD·AE=

AB·AC，∴AD²=DB·DC－AB·AC。　 3．证明：(1)∵BC是⊙A的直径，∴∠CMB=90⁰，∵BM是⊙B的半径，∴CM是⊙B的切线；　 (2)∵AB=AC=2，BM=1，∴BC=4，∴CM=，∵BC垂直平分MN，∴MN=2PM；在Rt△BCM中，BC·PM=CM·BM，∴PM=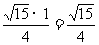，∴MN=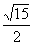。　 4．证明：(1) ∵AB是⊙O的直径，∴∠AEB=90⁰，∵BE是⊙B的半径，∴AE是⊙B的切线；(2)连结DF，∵BE=BC，∴∠BEC=∠BCE，∵AD垂直平分EF，∴DE=DF，∴∠DEF=∠DFE，∵∠BCE=∠DFE，∴△BCE∽△DFE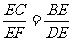，∴，∴BE·EF=CE·DF。(3)∵tg∠EDC=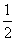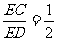，∴，设CE=a，则DE=2a，∴CD=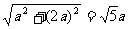，在Rt△CDE中，∵EF⊥CD，∴DE²=DM·CD，∴MD=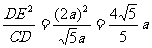，∴BM=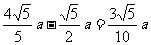

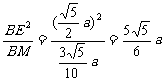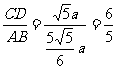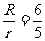在Rt△ABE中，∵∠AEB=90⁰，EF⊥AB，∴BE²=BM·AB，∴AB=，∴，即 ，∴R=。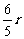

6、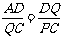证　　 　　　　　　 可得△ADQ≌△QCP；7、(1)(略)(2)DG=8；8、证∠E＝∠F可得

△CEF是等腰三角形；(2)(略)；

1、证△BOD≌△COE，可得OB=OC；2、∠B:∠C=2:1 ；3、△ACE≌△BCD，(证明过程略)；4、(1)证△AEC≌△CDB，得AE=CD；(2)BD=6；5、(略)；

2．解：如图：由题意知：∠BAC=120⁰， AB=AC，BD=30

AD⊥BC，∴∠B=30⁰，在Rt△ABD中，AD=BD·tgB=30×tg30⁰=30×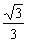≈17.3 (cm)。

∴∠F=∠A。