
9.如果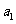 ,
,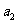 ,…,
,…,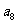 为各项都大于零的等差数列,公差
为各项都大于零的等差数列,公差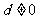 ,则__________.
,则__________.
①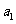
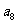
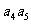 ②
②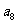
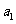
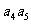 ③
③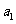 +
+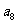
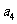 +
+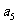 ④
④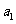
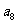 =
=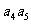
8.已知等差数列{an}满足α1+α2+α3+…+α101=0则有___________.
①α1+α101>0 ②α2+α100<0 ③α3+α99=0 ④α51=51
7.设Sn是等差数列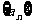 的前n项和,若
的前n项和,若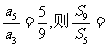 ______________.
______________.
6.等差数列{an}中,a1=1,a3+a5=14,其前n项和Sn=100,则n=______________.
5.等差数列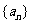 中,已知
中,已知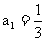 ,
,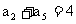 ,
,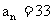 ,则n为______________.
,则n为______________.
3.设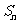 是等差数列
是等差数列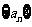 的前
的前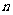 项和,若
项和,若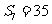 ,则
,则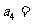 ________________.
________________.
4记等差数列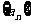 的前n项和为
的前n项和为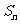 ,若
,若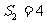 ,
,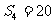 ,则该数列的公差d=_______.
,则该数列的公差d=_______.
1.等差数列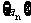 的前
的前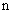 项和为
项和为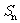 ,若
,若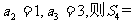 _______________.
_______________.
2已知{an}为等差数列,a2+a8=12,则a5等于________________.
20.本题主要考查二次函数的基本性质、不等式的基本性质与解法,以及综合运用所学知识分析和解决问题的能力。满分 14分。
证明:(Ⅰ)若 a = 0, 则 b = -c ,
f (0) f (1) = c (3a + 2b + c ) 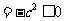 ,与已知矛盾, 所以 a ≠ 0.
,与已知矛盾, 所以 a ≠ 0.
方程 = 0 的判别式
= 0 的判别式 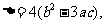 由条件 a + b + c = 0,消去 b,得
由条件 a + b + c = 0,消去 b,得
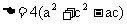
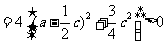 故方程 f (x) = 0 有实根.
(Ⅱ)由
故方程 f (x) = 0 有实根.
(Ⅱ)由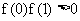 ,可知
,可知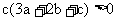
又a + b + c = 0,所以
所以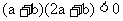 ,又a ≠ 0. 所以
,又a ≠ 0. 所以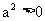
所以 ,解得
,解得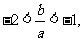
(Ⅲ)由条件,知
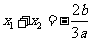 ,
, 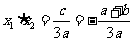 ,
,
所以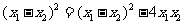
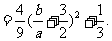 因为
因为 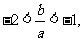 所以
所以 
故 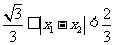
19.解法1:(Ⅰ)令g(x)=f(x)-x=x2+(a-1)x+a,则由题意可得

故所求实数a的取值范围是(0,3-2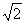 ).
).
(Ⅱ)f(0),f(1)-f(0)=g(0)g(1)=2a2, 令h(a)=2a2.
∵当a>0时h(a)单调增加,
∴当0<a<3-2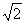 时
时
0<h(a)<h(3-2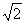 )=2(3-2
)=2(3-2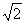 )2=2(17-12
)2=2(17-12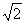 )=2·
)=2·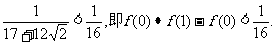
解法2:(Ⅰ)同解法1.
(Ⅱ)∵f(0)f(1)-f(0)=g(0)g(1)=2a2,由(Ⅰ)知0<a<3-2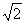
∴4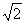 a-1<12
a-1<12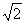 -17<0,又4
-17<0,又4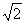 a+1>0,于是
a+1>0,于是
2a2-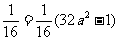 =
=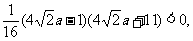
即2a2-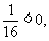 故f(0)f(1)-f(0)<
故f(0)f(1)-f(0)<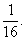
解法3:(Ⅰ)方程f(x)-x=0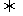 x2+(a-1)x+a=0,由韦达定理得
x2+(a-1)x+a=0,由韦达定理得

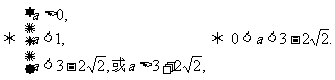
故所求实数a的取值范围是(0,3-2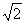 )
)
(Ⅱ)依题意可设g(x)=(x-x1)(x-x2),则由0<x1<x2<1得
f(0)f(1)-f(0)=g(0)g(1)=x1x2(1-x1)(1-x2)=[x1(1-x1)][x2(1-x2)]
<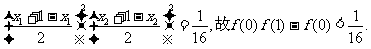
18.解: (1) 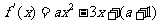 ,由于函数
,由于函数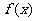 在
在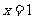 时取得极值,所以
时取得极值,所以 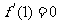
即 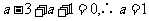
(2) 方法一:由题设知: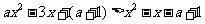 对任意
对任意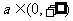 都成立
都成立
即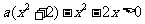 对任意
对任意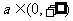 都成立
都成立
设 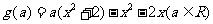 , 则对任意
, 则对任意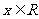 ,
, 为单调递增函数
为单调递增函数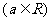
所以对任意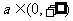 ,
,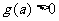 恒成立的充分必要条件是
恒成立的充分必要条件是
即 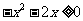 ,
,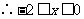
于是 的取值范围是
的取值范围是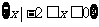
方法二:由题设知: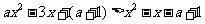 对任意
对任意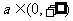 都成立
都成立
即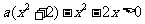 对任意
对任意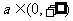 都成立
都成立
于是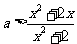 对任意
对任意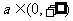 都成立,即
都成立,即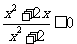
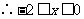
于是 的取值范围是
的取值范围是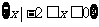
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com