
7.(天津市天津一中2010届高三第四次月考文科)若双曲线 的离心率是
的离心率是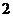 ,则实数
,则实数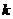 的值是( B )
的值是( B )
A. B.
B. 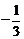 C.
C.
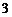
 D.
D.

10. (天津市天津一中2010届高三第四次月考理科)已知抛物线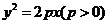 与双曲线
与双曲线 有相同的焦点
有相同的焦点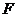 ,点
,点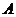 是两曲线的一个交点,且
是两曲线的一个交点,且 轴,若
轴,若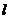 为双曲线的一条渐近线,则
为双曲线的一条渐近线,则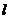 的倾斜角所在的区间可能是( D )
的倾斜角所在的区间可能是( D )
A. B.
B.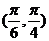 C.
C.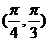 D.
D.
3.(天津市六校2010届高三第三次联考文科)已知双曲线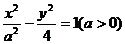 的右焦点与抛物线
的右焦点与抛物线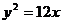 的焦点重合,则该双曲线的离心率为 ( B )
的焦点重合,则该双曲线的离心率为 ( B )
A. B.
B. C.
C.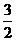 D.
D.
3.(天津市武清区2009-2010学年高三下学期第一次模拟文)若 ,则方程
,则方程 表示焦点在
表示焦点在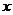 轴上的双曲线的充要条件是( A )
轴上的双曲线的充要条件是( A )
A.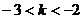 B.
B.
C. 或
或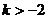 D.
D.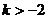
4.(天津市武清区2009-2010学年高三下学期第一次模拟理)若双曲线的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为( A )
A. B.5
B.5
C. D.2
D.2
9.(天津十二区县重点中学2010年高三联考一理)已知抛物线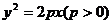 上一点
上一点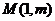
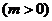 到其焦点的距离为
到其焦点的距离为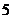 ,双曲线
,双曲线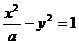 的左顶点为
的左顶点为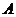 ,若双曲线一条渐近线与直线
,若双曲线一条渐近线与直线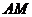 平行,则实数
平行,则实数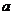 等于(A )
等于(A )
A.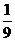 B.
B. C.
C.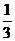 D.
D.
20. 解:(1)当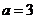 时,
时, ,
,
 ,
,
令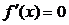 ,得
,得 或
或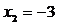 ,
,
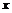 |
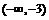 |
 |
 |
1 |
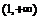 |
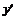 |
+ |
0 |
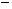 |
0 |
+ |
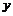 |
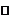 |
极大值 |
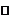 |
极小值 |
 |
所以,函数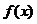 在
在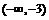 单调增,在
单调增,在 单调减,在
单调减,在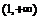 单调增.
单调增.
当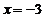 时,
时,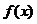 的极大值为
的极大值为 ;
;
当 时,
时,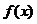 的极小值为
的极小值为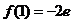 .
.
(2)由题设知 为
为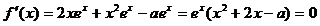 的两个根,
的两个根,
则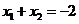 ,
,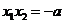 ,由
,由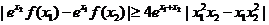 ,
,
得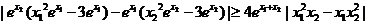 ,
,
 ,
,
 ,
,
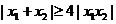 ,即
,即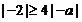 ,所以,
,所以, ,
,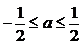 .
.
又 恒成立,
恒成立,
所以 恒成立,
恒成立,
令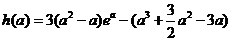 ,
,
则 ,
,
当 时,
时,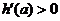
 ,
,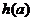 为增函数,
为增函数,
当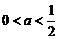 时,
时,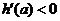
 ,
,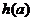 为减函数,
为减函数,
所以 时,函数
时,函数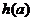 的极大值为
的极大值为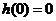 ,当
,当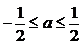 ,函数
,函数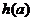 的最大值为0,所以
的最大值为0,所以 .
.
20.(天津市天津一中2010届高三第四次月考文科)设函数 .
.
(1)若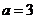 ,求
,求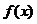 的单调区间和极值;
的单调区间和极值;
(2)若 为
为
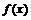 的两个不同的极值点,且
的两个不同的极值点,且
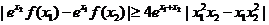 ,
, 恒成立,求实数
恒成立,求实数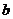 的取值范围.
的取值范围.
20、解:(1)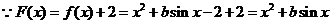 ,
,
依题意,对任意实数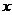 ,恒有
,恒有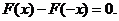
即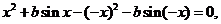
即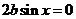
所以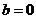 ,……………………(1分)
,……………………(1分)
所以 …………………… (2分)
…………………… (2分)
(2)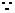
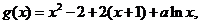
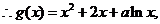
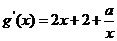 ……………………(3分)
……………………(3分)
 函数
函数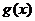 在(0,1)上单调递减,
在(0,1)上单调递减,
 在区间(0,1)
在区间(0,1)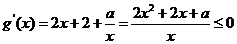 恒成立……………………(4分)
恒成立……………………(4分)
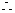
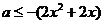 在(0,1)上恒成立
在(0,1)上恒成立
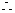 而
而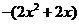 在(0,1)上单调递减
在(0,1)上单调递减
 为所求。……………………(6分)
为所求。……………………(6分)
(3)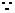
 =
=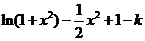 [来源:]
[来源:]

令 =0,解得
=0,解得
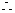 当
当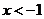 时,
时, 当
当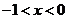 时,
时,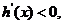
当 时,
时, 当
当 时,
时,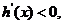
 ……………………(7分)
……………………(7分)
 ……………………(8分)
……………………(8分)
所以①当 时,函数没有零点;……………………(9分)
时,函数没有零点;……………………(9分)
②当 时,函数有四个零点;……………………(10分)
时,函数有四个零点;……………………(10分)
③当 或
或 时,函数有两个零点;……………………(11分)
时,函数有两个零点;……………………(11分)
④当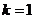 时,函数有三个零点;……………………(12分)
时,函数有三个零点;……………………(12分)
20.(天津市天津一中2010届高三第四次月考理科)已知函数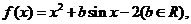
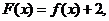 且对于任意实数
且对于任意实数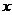 ,恒有
,恒有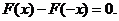
(1)求函数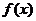 的解析式;
的解析式;
(2)已知函数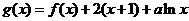 在区间
在区间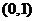 上单调递减,求实数
上单调递减,求实数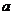 的取值范围;
的取值范围;
(3)函数 有几个零点?
有几个零点?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com