
21. (本题满分12分)已知函数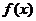 是在
是在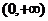 上每一点均可导的函数,若
上每一点均可导的函数,若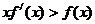 在
在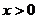 时恒成立.
时恒成立.
(1)求证:函数 在
在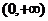 上是增函数;
上是增函数;
(2)求证:当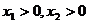 时,有
时,有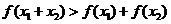 ;
;
(3)请将(2)问推广到一般情况,并证明你的结论.
20.(本题满分12分)已知函数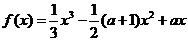
 ,函数
,函数
(1)判断方程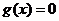 的零点个数;
的零点个数;
(2)解关于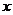 的不等式
的不等式 ,并用程序框图表示你的求解过程.
,并用程序框图表示你的求解过程.
19.(本题满分12分)已知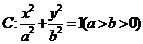 椭圆具有性质:若
椭圆具有性质:若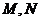 是椭圆上关于原点
是椭圆上关于原点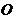 对称的两点,点
对称的两点,点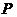 是椭圆上任意一点,当直线
是椭圆上任意一点,当直线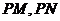 的斜率都存在,并记为
的斜率都存在,并记为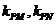 时,那么
时,那么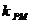 与
与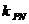 之积是与点
之积是与点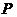 的位置无关的定值,试写出双曲线
的位置无关的定值,试写出双曲线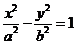 具有类似特性的性质并加以证明.
具有类似特性的性质并加以证明.
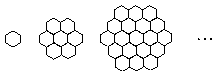
18.(本题满分12分)蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图. 其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以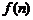 表示第
表示第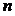 幅图的蜂巢总数.
幅图的蜂巢总数.
(1) 试给出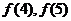 的值,并求
的值,并求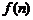 的表达式(不要求证明);
的表达式(不要求证明);
(2) 证明: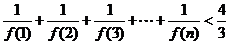 .
.
16.某同学准备用反证法证明如下一个问题:函数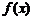 在
在 上有意义,且
上有意义,且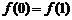 ,如果对于不同的
,如果对于不同的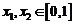 ,都有
,都有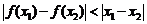 ,求证:
,求证: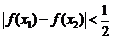 。那么他的反设应该是___________.
。那么他的反设应该是___________.
15.观察下列等式:
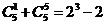 ,
,
 ,
,
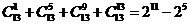 ,
,
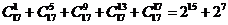 ,
,
………
由以上等式推测到一个一般的结论:
对于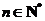 ,
,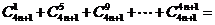 .
.
14.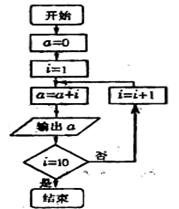 数列
数列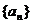 的前
的前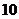 项由如图所示的流程图依次输出的
项由如图所示的流程图依次输出的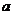 的值构成,则数列
的值构成,则数列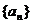 的一个通项公式
的一个通项公式 。
。
13.定义: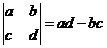 ,若复数
,若复数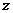 满足
满足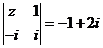 ,则
,则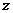 等于
.
等于
.
12. (2009浙江)10.对于正实数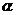 ,记
,记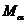 为满足下述条件的函数
为满足下述条件的函数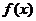 构成的集合:
构成的集合: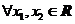 且
且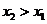 ,有
,有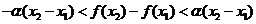 .下列结论中正确的是 ( )
.下列结论中正确的是 ( )
A.若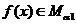 ,
,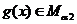 ,则
,则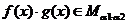
B.若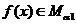 ,
,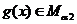 ,且
,且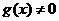 ,则
,则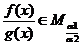
C.若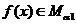 ,
,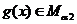 ,则
,则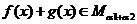
D.若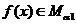 ,
,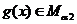 ,且
,且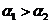 ,则
,则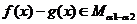
第Ⅱ卷(非选择题,共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com