
5. 自然状态下的鱼类是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能
力及捕捞强度对鱼群总量的影响. 用xn表示某鱼群在第n年年初的总量,n∈N*,且x1>0.
不考虑其它因素,设在第n年内鱼群的繁殖量及捕捞量都与xn成正比,死亡量与xn2成正比,
这些比例系数依次为正常数a,b,c.
(1)求xn+1与xn的关系式;
(2)猜测:当且仅当x1,a,b,c满足什么条件时,每年年初鱼群的总量保持不变?
(3)设a=2,c=1,为保证对任意x1∈(0,2),都有xn>0,n∈N*,则捕捞强度b的
最大允许值是多少?证明你的结论.
4.已知不等式 为大于2的整数,
为大于2的整数, 表示不超过
表示不超过 的最大整数. 设数列
的最大整数. 设数列 的各项为正,且满足
的各项为正,且满足 证明
证明 .
.
3.已知数列

证明 .
.
2.已知数列{ }的前n项和
}的前n项和 ,则{
,则{ }的前四项依次为_______,猜想
}的前四项依次为_______,猜想 =__________.
=__________.
1.用数学归纳法证明等式“1+2+3+…+( +3)=
+3)= (
(
 N)”,
N)”,
当 =1时,左边应为____________.
=1时,左边应为____________.
[例1] { }是正数组成的数列,其前n项和为
}是正数组成的数列,其前n项和为 ,并且对于所有的自然数
,并且对于所有的自然数 ,
, 与2的等差中项等于
与2的等差中项等于 与2的等比中项.
与2的等比中项.
(1)写出数列{ }的前3项;
}的前3项;
(2)求数列{ }的通项公式(写出推证过程);
}的通项公式(写出推证过程);
错解:由(1)猜想数列{ }有通项公式
}有通项公式 =4
=4 -2.
-2.
下面用数学归纳法证明数列{ }的通项公式是
}的通项公式是
 =4
=4 -2. (
-2. ( ∈N).
∈N).
①当 =1时,因为4×1-2=2,又在(1)中已求出
=1时,因为4×1-2=2,又在(1)中已求出 =2,所以上述结论成立.
=2,所以上述结论成立.
②假设n=k时结论成立,即有 =4
=4 -2.由题意,有
-2.由题意,有
将 =4
=4 -2代入上式,得
-2代入上式,得 ,解得
,解得

由题意,有
将 代入,化简得
代入,化简得

解得 .∴
.∴
这就是说,当n=k+1时,上述结论成立.
根据①、②,上述结论对所有的自然数n成立.
错因在于解题过程中忽视了取值的取舍.
正解:由(1)猜想数列{an}有通项公式an=4n-2.
猜想数列{ }有通项公式
}有通项公式 =4
=4 -2.
-2.
下面用数学归纳法证明数列{ }的通项公式是
}的通项公式是
 =4
=4 -2. (
-2. ( ∈N).
∈N).
①当 =1时,因为4×1-2=2,又在(1)中已求出
=1时,因为4×1-2=2,又在(1)中已求出 =2,所以上述结论成立.
=2,所以上述结论成立.
②假设n=k时结论成立,即有 =4
=4 -2.由题意,有
-2.由题意,有
将 =4
=4 -2代入上式,得
-2代入上式,得 ,解得
,解得

由题意,有
将 代入,化简得
代入,化简得

解得 .由
.由 ∴
∴
这就是说,当n=k+1时,上述结论成立.
根据①、②,上述结论对所有的自然数n成立.
[例2] 用数学归纳法证明对于任意自然数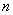 ,
,
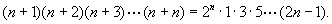
错解:证明:假设当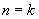 (
( N)时,等式成立,
N)时,等式成立,
即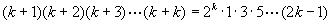 ,
,
那么当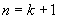 时,
时,
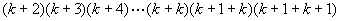
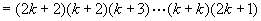
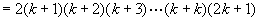
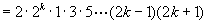
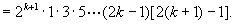
这就是说,当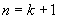 时,等式成立.
时,等式成立.
可知等式对任意 N成立.
N成立.
错因在于推理不严密,没有证明当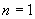 的情况
.
的情况
.
正解:证明:(1)当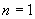 时,左式
时,左式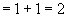 ,右式
,右式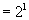 ,所以等式成立.
,所以等式成立.
(2)假设当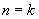 (
(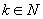 )时,等式成立,
)时,等式成立,
即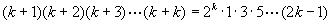 ,
,
那么当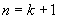 时,
时,
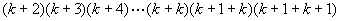
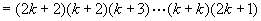
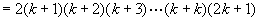
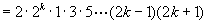
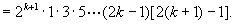
这就是说,当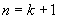 时,等式成立.
时,等式成立.
由(1)、(2),可知等式对任意 N成立.
N成立.
[例3] 是否存在自然数 ,使得
,使得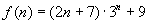 对任意自然数
对任意自然数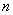 ,都能被
,都能被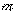 整除,若存在,求出
整除,若存在,求出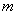 的最大值,并证明你的结论;若不存在,说明理由.
的最大值,并证明你的结论;若不存在,说明理由.
分析 本题是开放性题型,先求出 ,
, ,
, …再归纳、猜想、证明.
…再归纳、猜想、证明.
解: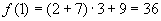 ,
,
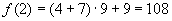 ,
,
 ,
,
……
猜想, 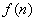 能被36整除,用数学归纳法证明如下:
能被36整除,用数学归纳法证明如下:
(1)当 时,
时,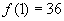 ,能被36整除.
,能被36整除.
(2)假设当 ,(
,( N)时,
N)时,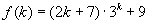 能被36整除.
能被36整除.
那么,当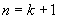 时,
时,
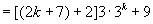
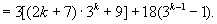
由归纳假设, 能被36整除,
能被36整除,
当 为自然数时,
为自然数时,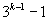 为偶数,则
为偶数,则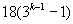 能被36整除.
能被36整除.
∴ 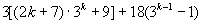 能被36整除,
能被36整除,
这就是说当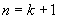 时命题成立.
时命题成立.
由(1)、(2)对任意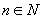 ,
, 都能被36整除.
都能被36整除.
当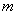 取大于36的自然数时,
取大于36的自然数时, 不能被
不能被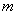 整除,所以36为最大.
整除,所以36为最大.
[例4] 设点 是曲线C:
是曲线C: 与直线
与直线 的交点,过
的交点,过 点作直线
点作直线 的垂线交
的垂线交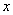 轴于
轴于 ,过
,过 点作直线
点作直线 的平行线交曲线C于
的平行线交曲线C于 ,再过
,再过 点作
点作
 的垂线作交X轴于
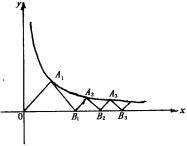
的垂线作交X轴于 ,如此继续下去可得到一系列的点
,如此继续下去可得到一系列的点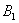 ,
,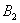 ,…,
,…,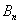 ,…如图,试求
,…如图,试求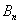 的横坐标
的横坐标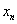 的通项公式.
的通项公式.
分析 本题并没有指明求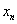 通项公式的方法,可用归纳--猜想--证明的方法,也可以通过寻求
通项公式的方法,可用归纳--猜想--证明的方法,也可以通过寻求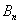 与
与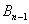 的递推关系式求
的递推关系式求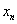 的通项公式.
的通项公式.
解:解法一 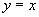 与
与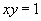 (
(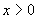 ,
,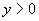 )联立,解得
)联立,解得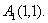
直线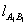 的方程为
的方程为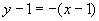 , 令
, 令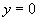 ,得
,得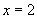 ,所以点
,所以点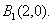
直线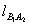 的方程为
的方程为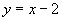 与
与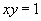 联立,消元得
联立,消元得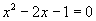 (
(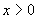 ),解得
),解得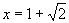 , 所以点
, 所以点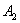 (
(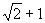 ,
,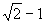 ).
).
直线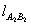 的方程为
的方程为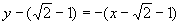 ,
,
令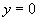 ,得
,得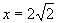 ,所以点
,所以点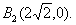 同样可求得点
同样可求得点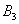 (
(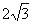 ,0)
,0)
……
由此推测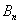 (
(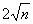 ,0),即
,0),即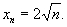
用数学归纳法证明
(1)当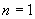 时,由
时,由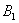 点的坐标为(
点的坐标为(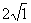 ,0),
,0),
即 ,所以命题成立.
,所以命题成立.
(2)假设当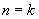 时命题成立,
时命题成立,
即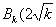 ,0),则当
,0),则当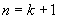 时,
时,
由于直线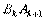 的方程为
的方程为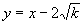 ,
,
把它与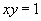 (
(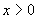 ,
,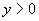 )联立,
)联立,
消去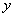 可得
可得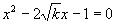 (
(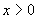 ),
),
∴ 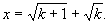
于是 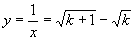
即点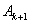 的坐标为(
的坐标为(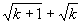 ,
,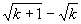 ).
).
∴ 直线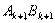 的方程为
的方程为
令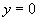 得,
得,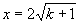
即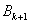 点的坐标为(
点的坐标为(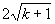 ,0)
,0)
∴ 当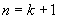 时,命题成立.
时,命题成立.
解法二 设点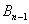 ,
,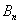 的坐标分别为(
的坐标分别为(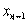 ,0)、(
,0)、(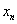 ,0),
,0),
建立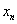 与
与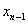 的递推关系
的递推关系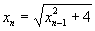 ,即
,即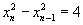 ,
,
由数列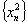 是等差数列,且
是等差数列,且 ,公差
,公差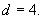
可求得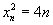 (
(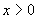 ),
),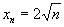 .
.
用数学归纳法证明与自然数n有关的几何命题,由k过渡到k+1常利用几何图形来分析图形前后演变情况.
[例5] 有n个圆,其中每两个圆都相交于两点,并且每三个圆都不相交于同一点,求证:这n个圆把平面分成f(n)=n2-n+2个部分.
证明①当n=1时,即一个圆把平面分成二个部分f(1)=2
又n=1时,n2-n+2=2,∴命题成立
②假设n=k时,命题成立,即k个圆把平面分成f(k)=k2-k+2个
部分,那么设第k+1个圆记⊙O,由题意,它与k个圆中每个圆
交于两点,又无三圆交于同一点,于是它与其它k个圆相交于2k
个点.把⊙O分成2k条弧而每条弧把原区域分成2块,因此这平
面的总区域增加2k块,即f(k+1)=k2-k+2+2k=(k+1)2-(k+1)+2
即n=k+1时命题成立.
由①②可知对任何n∈N命题均成立.
说明: 本题如何应用归纳假设及已知条件,其关键是分析k增加“1”时,研究第k+1个圆与其它k个圆的交点个数问题.
[例6] 已知n≥2,n∈N
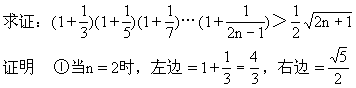
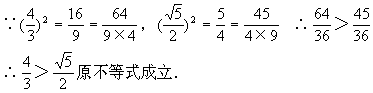
②假设n=k时,原不等式成立.
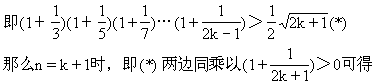
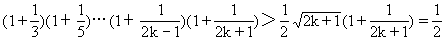
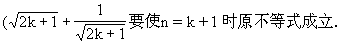
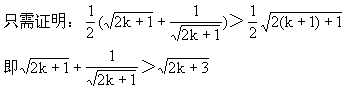
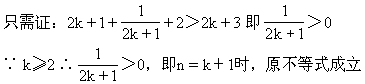
由①②可知,对任何n∈N(n≥2),原不等式均成立.
3. 数学归纳法是一种证明方法,归纳推理是一种推理方法.
2. 应用反证法证明命题的逻辑依据:做出与命题结论相矛盾的假定,由假定出发,应用正确的推理方法,推出矛盾的结果
1.归纳推理是根据一类事物的部分对象具有某种性质,推出这类事物的所有对象都具有这种性质的推理.
而类比推理是根据两类不同事物之间具有某些类似性,推出其中一类事物具有另一类事物类似的性质的推理.
14. 数学归纳法的步骤:
(1)证明当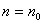 (如
(如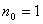 或2等)时,结论正确;
或2等)时,结论正确;
(2)假设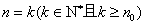 时结论正确,证明
时结论正确,证明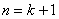 时结论也正确.
时结论也正确.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com