5．对于平面几何中的命题“如果两个角的两边分别对应垂直，那么这两个角相等或互补”，在立体几何中，类比上述命题可以得到命题__________，这个命题的真假性是______ .

4.设PA⊥Rt△ABC所在的平面α，∠BAC=90°，PB、PC分别与α成45°和30°角，PA=2，则PA与BC的距离是_____________；点P到BC的距离是_____________.

3.三棱锥V-ABC中，VA=BC，VB=AC，VC=AB，侧面与底面ABC所成二面角分别为α，β，γ(都是锐角)，则cosα+cosβ+cosγ等于 (　 )

　A.1　　 B.2　　　 C.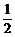　　 D.

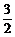
2.在△ABC中，AB=15，∠BCA=120°，若△ABC所在平面α外一点P到A、B、C的距离都是14，则P到α的距离是 　　　　　　(　 )

A.13　　 　 B.11　　 C.9　 　 D.7

1．在正△ABC中，AD⊥BC于D，沿AD折成二面角B-AD-C后，BC=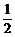AB，这时二面角B-AD-C大小为 　　　　　　　　　　(　 )

A．60⁰　 　B.90⁰ C.45⁰　 D.120⁰

3.常用计算公式

(1)　　　　　 S′=S.cosα　　　　

(2)　　　　　 cosθ=cosθ₁·cosθ₂

能想象上式中α，θ，θ₁，θ₂是什么角，S，S′表示什么吗？

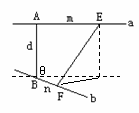
(3)　　 异面直线上两点间距离公式:

设异面直线a，b所成角为θ 则EF²=m²+n²+d²±2mncosθ

2．距离有七种，即点点、点线、两条平行直线、两条异面直线、点到平面、平行于平面的直线与该平面、两个平行平面之间的距离.

空间角和距离的求法,概括地讲都是转化为平面几何几何问题求解,或利用下列计算公式.

1．空间的三种角，即异面直线所成角、直线与平面所成角。平面与平面所成二面角.

3．能利用这些概念和方法进行论证和解决有关问题.

2.掌握空间中各种距离的概念和求法；