
4.取特殊位置
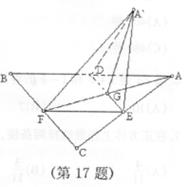 例7.(2008宁夏区银川一中)如图,边长为
例7.(2008宁夏区银川一中)如图,边长为 的正
的正 中线
中线 与中位线
与中位线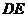 相交于
相交于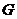 ,已知
,已知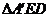 是
是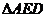 绕
绕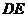 旋转过程中的一个图形,现给出下列命题,其中正确的命题
旋转过程中的一个图形,现给出下列命题,其中正确的命题
有 (填上所有正确命题的序号)
(1)动点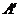 在平面
在平面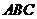 上的射影在线段
上的射影在线段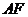 上;
上;
(2)三棱锥 的体积有最大值;
的体积有最大值;
(3)恒有平面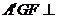 平面
平面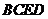 ;
;
(4)异面直线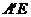 与
与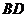 不可能互相垂直;
不可能互相垂直;
分析:由于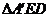 是
是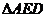 绕
绕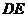 旋转过程中的一个图形,可以转动到特殊位置,需要考虑特殊情况.
旋转过程中的一个图形,可以转动到特殊位置,需要考虑特殊情况.
解: 不论怎样转动, ,(1)(3)正确,(2)
,(1)(3)正确,(2)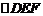 不再变化,当高最大时,三棱锥
不再变化,当高最大时,三棱锥 的体积有最大值,即当
的体积有最大值,即当 时, 三棱锥
时, 三棱锥 的体积有最大值也正确,(4)不正确,由三垂线定理知,当
的体积有最大值也正确,(4)不正确,由三垂线定理知,当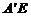 在平面
在平面 内的射影与
内的射影与 平行时就一定垂直.
平行时就一定垂直.
评注:特殊位置法是解决变化的图形的一种策略,要想到一些特殊位置.
例8.(福建省八闽高中)某校高三年级老师到外校参观学习2天,留下6位老师值班,记每天上午、下午、晚上各为一“工作时”,则每位老师必须且只需值班一个“工作时”,由于有事,甲老师不能值晚班,乙老师不能值下午班,那么年级值班排法共有…………………………………( )
A.288种 B.312种 C.336种 D.360种
分析:甲老师、乙老师都有特殊要求,应该先满足他们的特殊要求先排,如果先排甲老师,则由于他排在上午和下午会影响到乙老师的排法,所以需要分类讨论。
解:先排甲老师有两种情况,(1)甲老师排在上午值班,有2种方法,乙老师排在晚上值班也有2种方法,其余4位老师有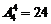 种方法,共2×2×24=96种方法。(2)甲老师排在下午值班,有2种方法,乙老师与其他4位老师随便排都可以,有
种方法,共2×2×24=96种方法。(2)甲老师排在下午值班,有2种方法,乙老师与其他4位老师随便排都可以,有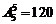 种方法,共有240种方法;由(1)(2)可知共336种方法。
种方法,共有240种方法;由(1)(2)可知共336种方法。
评注:本题为排列组合的特殊元素和特殊位置题,按特殊元素和特殊位置优先的原则,分情况讨论。
3.取特殊数列
例6.(2008四川卷,理7)已知等比数列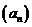 中
中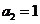 ,则其前3项的和
,则其前3项的和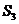 的取值范围是( )
的取值范围是( )
(A)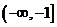 (B)
(B)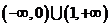
(C)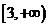 (D)
(D)
分析:本题中的等比数列只知道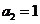 ,如果再知道公比,数列就可以确定,而选项是范围问题,可取定公比加以排除。
,如果再知道公比,数列就可以确定,而选项是范围问题,可取定公比加以排除。
解法一:∵等比数列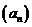 中
中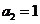 ∴当公比为1时,
∴当公比为1时,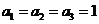 ,
,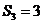 ;
;
当公比为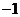 时,
时,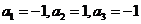 ,
, 从而淘汰(A)(B)(C)
从而淘汰(A)(B)(C)
故选D;
解法二:∵等比数列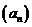 中
中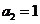 ∴
∴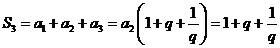
∴当公比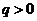 时,
时, ;
;
当公比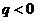 时,
时,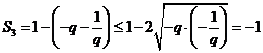
∴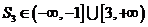 故选D;
故选D;
评注:取特殊数列入手淘汰,如果一次不能区分,则需多次取有区分度的值进行排除,直至能辨别出正确答案为止,也可多种方法并存。要重视等比数列的通项公式,前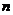 项和公式,以及均值不等式的应用,特别注重均值不等式使用的条件是否具备,不具备就要进行分类讨论。
项和公式,以及均值不等式的应用,特别注重均值不等式使用的条件是否具备,不具备就要进行分类讨论。
2.取特殊函数
例4.(2008陕西卷,理11.改编)定义在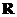 上的函数
上的函数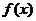 满足
满足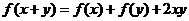 (
(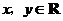 ),
),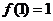 ,则
,则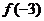 等于( )
等于( )
A.2 B.3 C.6 D.9
分析:由 及
及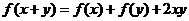 ,可令
,可令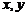 为特殊值,求出
为特殊值,求出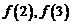 ,
,
再取特值研究函数的奇偶性;或直接取满足条件的特殊函数解答。
解法一:取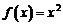 ,则满足
,则满足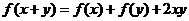 和
和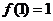 ,∴
,∴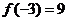 ,选D
,选D
解法二: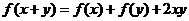 中,令
中,令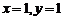 ,得
,得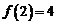 ,再令
,再令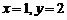 得
得 ,再令
,再令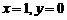 ,得
,得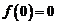 ,令
,令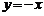 得,
得,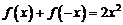 ,再令
,再令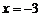 ,得
,得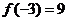 ,选D
,选D
评注:对于抽象函数来说,取特殊值和取特殊函数是常用的方法.
例5.(取特殊函数的三角题)
1.取特殊数值
例1.(2008重庆卷,理6)若定义在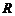 上的函数
上的函数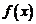 满足:对任意
满足:对任意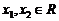 有
有 ,则下列说法一定正确的是(
)
,则下列说法一定正确的是(
)
(A) 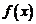 为奇函数(B)
为奇函数(B)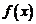 为偶函数(C)
为偶函数(C) 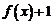 为奇函数(D)
为奇函数(D)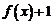 为偶函数
为偶函数
分析:判断函数的奇偶性需要用定义,即找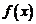 与
与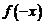 之间的关系,由于
之间的关系,由于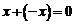 所以需要先求出
所以需要先求出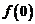 的值,这时需要取特殊值
的值,这时需要取特殊值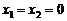 解答。
解答。
解:令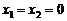 ,得
,得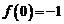 ,令
,令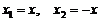 得
得 ∴
∴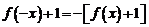 ,∴
,∴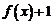 为奇函数,故选
为奇函数,故选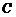
答案: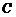
评注:在对于抽象函数来说,常常通过取特殊值研究函数的奇偶性。
例2.若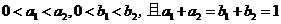 ,则下列代数式中值最大的是
,则下列代数式中值最大的是
A.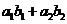 B.
B.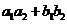 C.
C.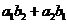 D.
D.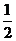
分析:本题比较大小,可以取特殊值,也可以作差比较,还可以用基本不等式或排序不等式。
解法一:特殊值法.取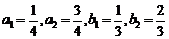 ,通过计算比较
,通过计算比较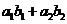 最大。选A
最大。选A
解法二: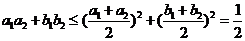
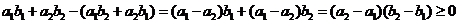

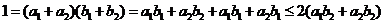

解法三:根据排序不等式知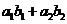 、
、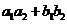 、
、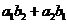 中,
中,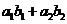 最大,再取特值
最大,再取特值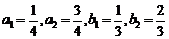 比较
比较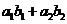 与
与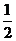
答案: A.
评注:本题中有多种做法,其中取特殊值法最简单,最直接。
例3(2008福建德化一中,理)已知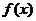 对一切实数
对一切实数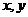 都有
都有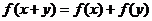 ,且当
,且当 >
>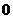 时,
时,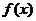 <
<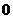
(1)证明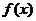 为奇函数且是
为奇函数且是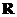 上的减函数;
上的减函数;
(2)若关于 的不等式
的不等式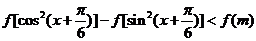 对一切
对一切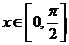 恒成立,求m的取值范围;
恒成立,求m的取值范围;
(3)如果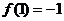 ,
,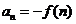 ,记数列
,记数列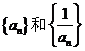 的前n项和分别为
的前n项和分别为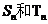 ,求证
,求证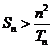
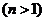
分析:本题中的函数为抽象函数,可通过取特殊值研究函数的单调性,再利用函数的单调性把不等式转化,得到关于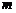 的不等式恒成立,有函数求的最值解答,
的不等式恒成立,有函数求的最值解答,
(1)证明:依题意取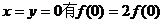
∴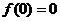 又取
又取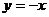 可得
可得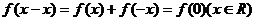
∴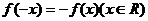 由x的任意性可知
由x的任意性可知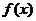 为奇函数
为奇函数
又设
∴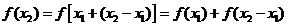
∵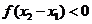 ∴
∴ ∴
∴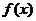 在R上减函数
在R上减函数
(2)解:∵函数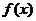 是奇函数,∴由
是奇函数,∴由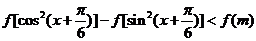
得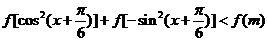
∴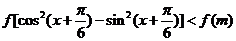 即
即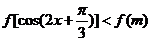
又∵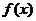 是
是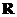 上的减函数 ∴
上的减函数 ∴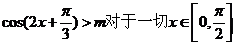 恒成立
恒成立
当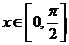 时,
时,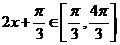 ,故此时
,故此时 的最小值为
的最小值为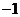 ,
,
∴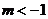
(3)∵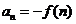 ∴
∴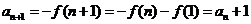
又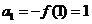 ,∴数列
,∴数列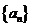 是以1为首项,以1为公差的等差数列,
是以1为首项,以1为公差的等差数列,
∴ , 要证明不等式
, 要证明不等式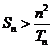 ,即是证明
,即是证明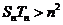
也就是证明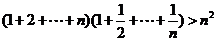 由柯西不等式得
由柯西不等式得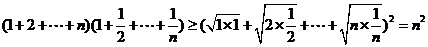
要使不等式取得等号,当且仅当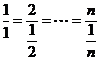 ,而这是不可能成立的。
,而这是不可能成立的。
∴当 时,
时, ,即
,即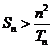
评注:研究抽象函数的单调性常用取特殊值法,本题较为综合的考查了抽象函数的单调性以及利用函数的单调性解得不等式及函数的最值,还有把函数问题转化为数列,最终利用柯西不等式证出。
(二)考点预测题
1.(2007天津 理工13)设等差数列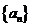 的公差
的公差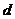 是2,前
是2,前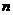 项的和为
项的和为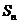 ,则
,则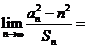 .
.
[解析]本题设出首项,表示出通项和前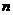 和(有限项),然后代入求极限.而在求极限的时候,利用到已经掌握的极限知识
和(有限项),然后代入求极限.而在求极限的时候,利用到已经掌握的极限知识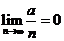 和
和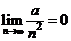 ,其中
,其中 为常数.
为常数.
[答案]设首项为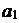 ,则
,则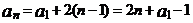 ,
,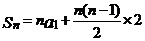
 ,
,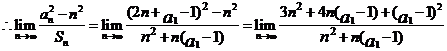
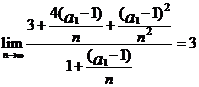 .
.
2.(2008山东卷 文20)将数列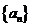 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表:
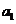
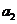
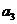
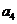
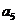
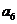
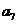
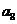
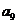
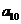
......
记表中的第一列数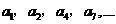 构成的数列为
构成的数列为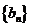 ,
,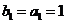 .
.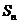 为数列
为数列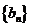 的前
的前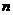 项和,且满足
项和,且满足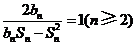 .
.
(Ⅰ)证明数列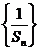 成等差数列,并求数列
成等差数列,并求数列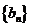 的通项公式;
的通项公式;
(Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当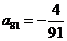 时,求上表中第
时,求上表中第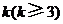 行所有项的和.
行所有项的和.
[解析]第(Ⅰ)问从无穷数列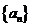 中抽出它的一个无穷的子数列,由
中抽出它的一个无穷的子数列,由 与
与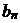 的递推关系式消去
的递推关系式消去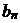 ,从而证明
,从而证明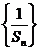 是无穷的等差数列. 第(Ⅱ)问就是求从第三行起的每一行所有的这些无穷多项的和.
是无穷的等差数列. 第(Ⅱ)问就是求从第三行起的每一行所有的这些无穷多项的和.
[答案](Ⅰ)证明:由已知,当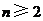 时,
时,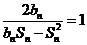 ,
,
又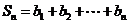 ,所以
,所以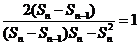 ,
,
即 ,所以
,所以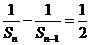 ,
,
又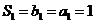 .所以数列
.所以数列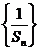 是首项为1,公差为
是首项为1,公差为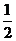 的等差数列.
的等差数列.
由上可知 ,即
,即 .
.
所以当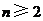 时,
时,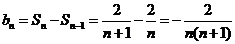 .
.
因此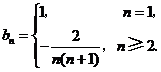
(Ⅱ)解:设上表中从第三行起,每行的公比都为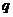 ,且
,且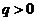 .
.
因为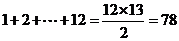 ,所以表中第1行至第12行共含有数列
,所以表中第1行至第12行共含有数列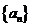 的前78项,
的前78项,
故 在表中第13行第三列,因此
在表中第13行第三列,因此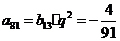 .
.
又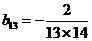 ,所以
,所以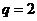 .
.
记表中第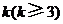 行所有项的和为
行所有项的和为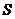 ,
,
则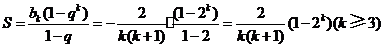


(一)考点预测
根据近几年各地高考试题和模拟试题来看,有限与无限的思想逐年增加考查广度,我们认为2009年的高考一定会有更多的体现.在题型上来看,热点问题仍然是以数列为载体考查极限的知识和用数学归纳法证题.
2.(安徽省皖南八校2008届高三第三次联考,数学,18)数列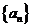 的首项
的首项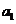 =1,前
=1,前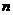 项和为
项和为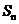 满足
满足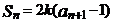 (常数
(常数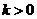 ,
,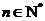 ).
).
(1)求证:数列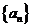 是等比数列.
是等比数列.
(2)设数列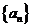 的公比为
的公比为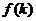 ,作数列
,作数列 ,使
,使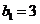 ,
,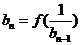 (
(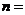 2,3,4,…)
2,3,4,…)
求数列 的通项公式;
的通项公式;
(3)设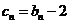 ,若存在
,若存在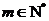 ,且
,且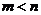 ;使
;使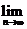 (
(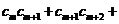 …
…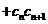 )
)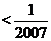 ,试求
,试求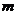 的最小值.
的最小值.
[解析]第(1)问通过对递推关系式的变形得到相邻两项的比,正是利用这两个有限项的比是非零常数来证明该数列是等比数列的.第(2)问也是通过对递推关系式(无限的问题)的变形来求通项公式的(无限的问题).第(3)问通过抓住通项来求有限项的极限,再根据这个极限求出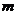 的最小值.
的最小值.
[答案] 解:(1)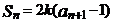 ①
①
当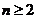 时,
时,  ②
②
①-②得,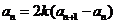 即
即
由①, 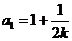 ,∴
,∴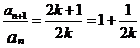 ,
,
又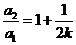 符合上式,∴
符合上式,∴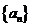 是以1为首项,
是以1为首项,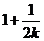 为公比的等比数列.
为公比的等比数列.
(2)由(1)知
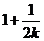 ,∴
,∴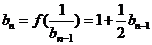 (
(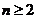 ),
),
∴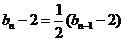 .又
.又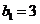 ,即
,即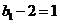 ,
,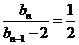 ,
,
∴数列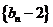 是为1首项,
是为1首项,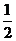 为公比的等比数列.
为公比的等比数列.
∴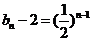 ,∴
,∴ .
.
(3)由(2)知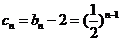 ,则
,则 .
.
∴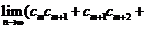 …
…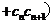 =
=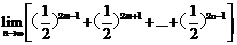
=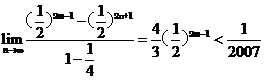 ,
,
∴ ,∴
,∴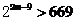 . ∵
. ∵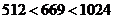 ,∴
,∴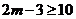 ,
, .
.
又∵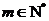 ,∴
,∴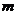 的最小值为7.
的最小值为7.
1.(福建省泉州一中2008届高三毕业班第二次模拟检测,数学,22)数列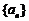 中,
中,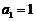 ,
,
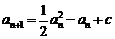 (
(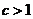 为常数,
为常数,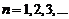 ) ,且
) ,且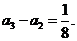
(1)求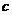 的值;
的值;
(2)①
证明: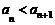 ;
;
② 猜测数列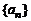 是否有极限?如果有,写出极限的值(不必证明);
是否有极限?如果有,写出极限的值(不必证明);
(3)比较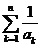 与
与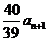 的大小,并加以证明.
的大小,并加以证明.
[解析]第(1)问由通项公式(揭示无限问题)求出有限项 后可得
后可得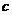 的值;第(2)问通过对有限项的处理证明出结论,从而可猜出
的值;第(2)问通过对有限项的处理证明出结论,从而可猜出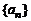 的极限;第(3)问对得到的递推关系式进行变形,再用作差法求解,需要用到数学归纳法证得
的极限;第(3)问对得到的递推关系式进行变形,再用作差法求解,需要用到数学归纳法证得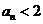 .然后通过前几项(有限项)的比较与第(2)问已证的单调性得到结果.
.然后通过前几项(有限项)的比较与第(2)问已证的单调性得到结果.
[答案](Ⅰ)依题意,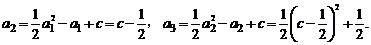
由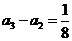 ,得
,得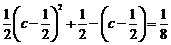 ,解得
,解得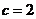 ,或
,或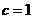 (舍去).
(舍去).
(Ⅱ)① 证明:因为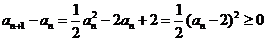 ,
,
当且仅当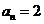 时,
时,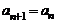 .因为
.因为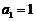 ,所以
,所以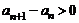 ,即
,即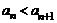 (
(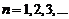 ).
).
②
数列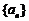 有极限,且
有极限,且 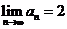 .
.
(Ⅲ)由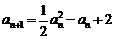 ,可得
,可得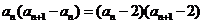 ,从而
,从而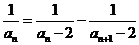 .
.
因为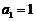 ,所以
,所以
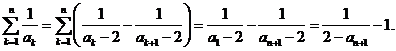
所以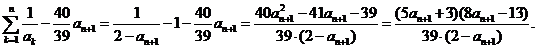
因为 ,由(Ⅱ)①
得
,由(Ⅱ)①
得 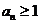 (
(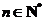 ). (*)
). (*)
下面用数学归纳法证明:对于任意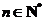 ,有
,有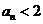 成立.
成立.
当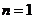 时,由
时,由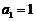 ,显然结论成立.
,显然结论成立.
假设结论对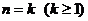 时成立,即
时成立,即
 因为
因为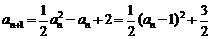 ,且函数
,且函数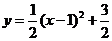 在
在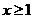 时单调递增,
时单调递增,
所以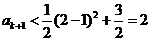 .即当
.即当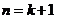 时,结论也成立. 于是,当
时,结论也成立. 于是,当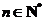 时,有
时,有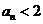 成立. (**)
成立. (**)
根据(*)及(**)得  .
.
由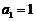 及
及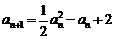 ,
经计算可得
,
经计算可得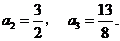
所以,当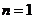 时,
时,
 ;当
;当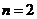 时,
时,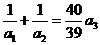 ;
;
当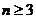 时,由
时,由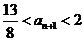 ,得
,得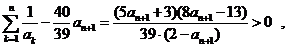
所以 .
.
3. (2008辽宁卷21)在数列
(2008辽宁卷21)在数列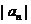 ,
,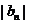 中,a1=2,b1=4,且
中,a1=2,b1=4,且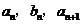 成等差数列,
成等差数列,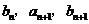 成等比数列(
成等比数列(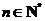 ).
).
(Ⅰ)求a2,a3,a4及b2,b3,b4,由此猜测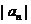 ,
,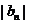 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(Ⅱ)证明: .
.
[解析]第(Ⅰ)问由题设可得两个数列的递推关系式,进而得到两个数列的前几项(有限项) ,可以猜出两者的通项公式(无限的问题),再用数学归纳法证明这个无限的问题.第(Ⅱ)问可以通过研究通项公式(无限的问题)直接解决无限的问题.
[答案](Ⅰ)由条件得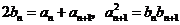 ,由此可得
,由此可得
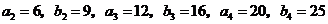 .猜测
.猜测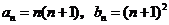 .
.
下面用数学归纳法证明:
①当n=1时,由上可得结论成立.
②假设当n=k时,结论成立,即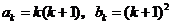 ,
,
那么当n=k+1时,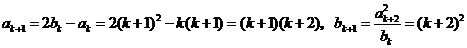 ,
,
所以当n=k+1时,结论也成立.
由①②,可知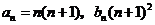 对一切正整数都成立.
对一切正整数都成立.
(Ⅱ)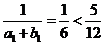 .n≥2时,由(Ⅰ)知
.n≥2时,由(Ⅰ)知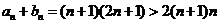 .
.
故
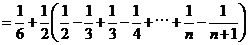
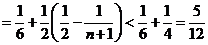 .
.
综上,原不等式成立.
2. (2005年福建卷,理,22) 已知数列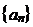 满足
满足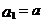 ,
,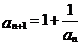 我们知道当a取不同的值时,得到不同的数列,如当
我们知道当a取不同的值时,得到不同的数列,如当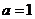 时,得到无穷数列:
时,得到无穷数列: 当
当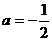 时,得到有穷数列:
时,得到有穷数列: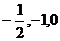 .
.
(Ⅰ)求当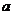 为何值时
为何值时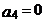 ;
;
(Ⅱ)设数列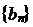 满足
满足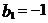 ,
, 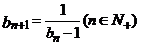 ,求证:
,求证: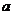 取数列
取数列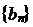 中的任一个数,都可以得到一个有穷数列
中的任一个数,都可以得到一个有穷数列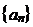 ;
;
(Ⅲ)若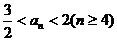 ,求
,求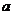 的取值范围.
的取值范围.
[解析] 这是一道蕴含有限与无限的思想的典型试题. 对于题设的递推关系,随着所给出的初始条件不同,得到的数列既可能是无限数列也可能是有限的数列,第(Ⅱ)问则可以通过有有限次的试验,得出对无限个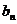 都可以得到一个有穷数列{an}的猜想,再用数学归纳法进行证明.或者通过对有限问题的推理直接得到无限问题的解答.第(Ⅲ)问是把对无限个
都可以得到一个有穷数列{an}的猜想,再用数学归纳法进行证明.或者通过对有限问题的推理直接得到无限问题的解答.第(Ⅲ)问是把对无限个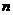 都成立的结果,通过有限次分析获得解决.
都成立的结果,通过有限次分析获得解决.
[答案](Ⅰ)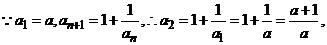

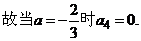
(Ⅱ) 解法一: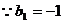 ,
,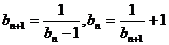 ,
,
当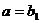 时,
时, ,
,
当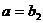 时,
时,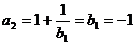 ,
,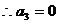 ,
,
当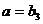 时,
时,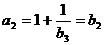 ,
,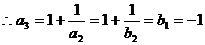
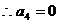 .
.
一般地, 当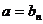 时,
时,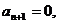 可得一个含有
可得一个含有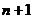 项的有穷数列
项的有穷数列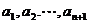 .
.
下面用数学归纳法证明.
(1)
当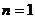 时,
时, 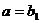 ,显然
,显然 ,可得一个含有2项的有穷数列
,可得一个含有2项的有穷数列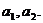
(2)
假设当 时,
时,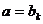 ,得到一个含有
,得到一个含有 项的有穷数列
项的有穷数列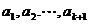 ,其中
,其中
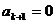 ,则
,则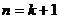 时,
时,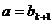 ,
,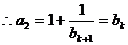 ,
,
由假设可知, 得到一个含有 项的有穷数列
项的有穷数列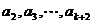 ,其中
,其中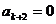 .
.
所以,当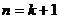 时, 可以得到一个含有
时, 可以得到一个含有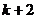 项的有穷数列
项的有穷数列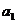 ,
,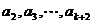 ,其中
,其中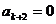
由(1),(2)知,对一切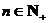 ,命题都成立.
,命题都成立.
解法二: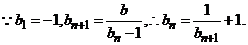

故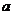 取数列
取数列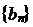 中的任一个数,都可以得到一个有穷数列
中的任一个数,都可以得到一个有穷数列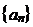 .
.
(Ⅲ)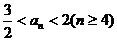 即
即 ,
,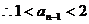
所以要使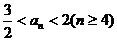 ,当且仅当它的前一项
,当且仅当它的前一项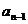 满足
满足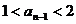 .
.
由于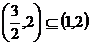 ,所以只须当
,所以只须当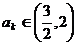 时,都有
时,都有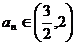
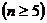
由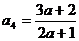 ,得
,得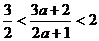 , 解得
, 解得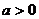 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com