
26.(2009安徽卷文)(本小题满分12分)
已知数列{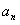 } 的前n项和
} 的前n项和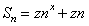 ,数列{
,数列{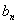 }的前n项和
}的前n项和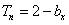
(Ⅰ)求数列{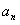 }与{
}与{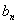 }的通项公式;
}的通项公式;
(Ⅱ)设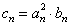 ,证明:当且仅当n≥3时,
,证明:当且仅当n≥3时,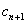 <
<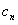 .
.


[思路]由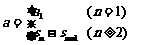 可求出
可求出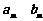 ,这是数列中求通项的常用方法之一,在求出
,这是数列中求通项的常用方法之一,在求出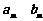 后,进而得到
后,进而得到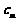 ,接下来用作差法来比较大小,这也是一常用方法。
,接下来用作差法来比较大小,这也是一常用方法。
[解析](1)由于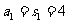
当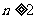 时,
时, 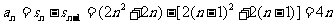
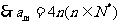
又当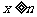 时
时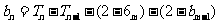
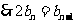
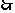 数列
数列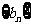 项与等比数列,其首项为1,公比为
项与等比数列,其首项为1,公比为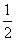
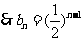 .
. 

(2)由(1)知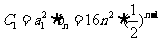
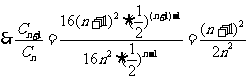
由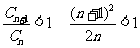 即
即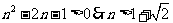 即
即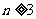
又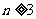 时
时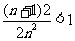 成立,即
成立,即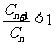 由于
由于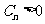 恒成立. .
恒成立. . 

因此,当且仅当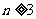 时,
时, 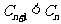
25.(2009安徽卷理)(本小题满分13分)
首项为正数的数列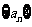 满足
满足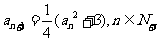


(I)证明:若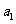 为奇数,则对一切
为奇数,则对一切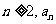 都是奇数;
都是奇数;
(II)若对一切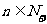 都有
都有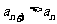 ,求
,求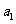 的取值范围.
的取值范围.
解:本小题主要考查数列、数学归纳法和不等式的有关知识,考查推理论证、抽象概括、运算求解和探究能力,考查学生是否具有审慎思维的习惯和一定的数学视野。本小题满分13分。
解:(I)已知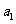 是奇数,假设
是奇数,假设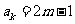 是奇数,其中
是奇数,其中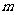 为正整数,
为正整数,
则由递推关系得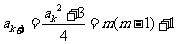 是奇数。
是奇数。 

根据数学归纳法,对任何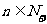 ,
,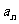 都是奇数。
都是奇数。
(II)(方法一)由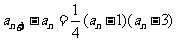 知,
知,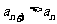 当且仅当
当且仅当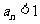 或
或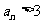 。
。
另一方面,若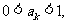 则
则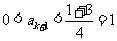 ;若
;若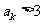 ,则
,则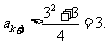
根据数学归纳法,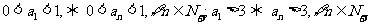
综合所述,对一切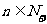 都有
都有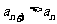 的充要条件是
的充要条件是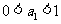 或
或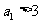 。
。
(方法二)由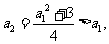 得
得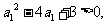 于是
于是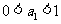 或
或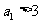 。
。
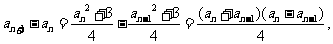


因为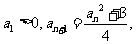 所以所有的
所以所有的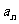 均大于0,因此
均大于0,因此 与
与 同号。
同号。
根据数学归纳法,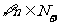 ,
, 与
与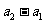 同号。
同号。 

因此,对一切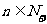 都有
都有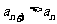 的充要条件是
的充要条件是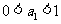 或
或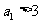 。
。
24.(2009广东卷理)(本小题满分14分). 

已知曲线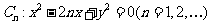 .从点
.从点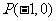 向曲线
向曲线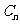 引斜率为
引斜率为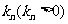 的切线
的切线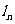 ,切点为
,切点为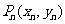 .
.
(1)求数列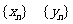 的通项公式;
的通项公式;
(2)证明: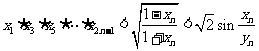 .
.
解:(1)设直线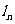 :
: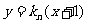 ,联立
,联立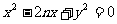 得
得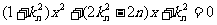 ,则
,则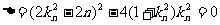 ,∴
,∴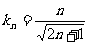 (
(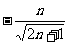 舍去).
舍去). 

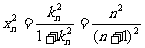 ,即
,即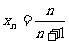 ,∴
,∴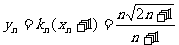
(2)证明:∵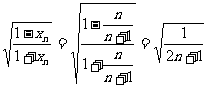 .
. 

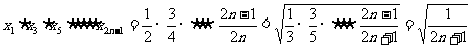
∴
由于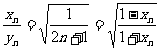 ,可令函数
,可令函数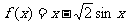 ,则
,则 ,令
,令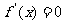 ,得
,得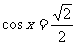 ,给定区间
,给定区间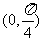 ,则有
,则有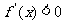 ,则函数
,则函数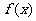 在
在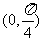 上单调递减,∴
上单调递减,∴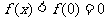 ,即
,即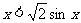 在
在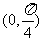 恒成立,又
恒成立,又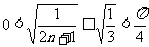 ,
,
则有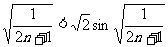 ,即
,即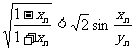 .
. 
 .
. 

23.(2009山东卷文)(本小题满分12分)
等比数列{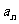 }的前n项和为
}的前n项和为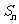 , 已知对任意的
, 已知对任意的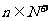 ,点
,点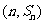 ,均在函数
,均在函数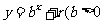 且
且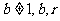 均为常数)的图像上.
均为常数)的图像上. 

(1)求r的值;
(11)当b=2时,记 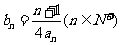 求数列
求数列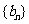 的前
的前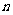 项和
项和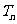
解:因为对任意的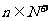 ,点
,点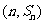 ,均在函数
,均在函数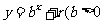 且
且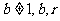 均为常数)的图像上.所以得
均为常数)的图像上.所以得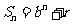 ,
,
当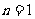 时,
时,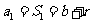 ,
, 

当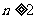 时,
时,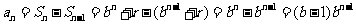 ,
,
又因为{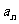 }为等比数列, 所以
}为等比数列, 所以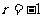 , 公比为
, 公比为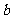 , 所以
, 所以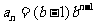
(2)当b=2时,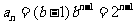 ,
, 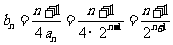
则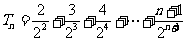
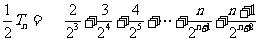


相减,得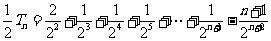
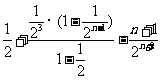
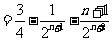
所以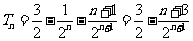
[命题立意]:本题主要考查了等比数列的定义,通项公式,以及已知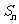 求
求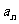 的基本题型,并运用错位相减法求出一等比数列与一等差数列对应项乘积所得新数列的前
的基本题型,并运用错位相减法求出一等比数列与一等差数列对应项乘积所得新数列的前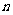 项和
项和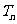 .
.
22.(2009山东卷理)(本小题满分12分)
等比数列{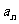 }的前n项和为
}的前n项和为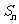 , 已知对任意的
, 已知对任意的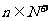 ,点
,点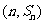 ,均在函数
,均在函数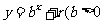 且
且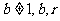 均为常数)的图像上.
均为常数)的图像上.
(1)求r的值;
(11)当b=2时,记 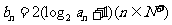 .
. 

证明:对任意的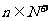 ,不等式
,不等式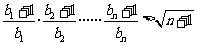 成立
成立
解:因为对任意的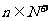 ,点
,点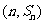 ,均在函数
,均在函数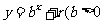 且
且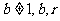 均为常数的图像上.所以得
均为常数的图像上.所以得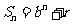 ,当
,当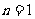 时,
时,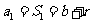 ,当
,当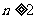 时,
时,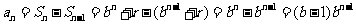 ,又因为{
,又因为{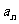 }为等比数列,所以
}为等比数列,所以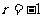 ,公比为
,公比为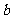 ,
,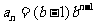
(2)当b=2时,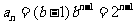 ,
, 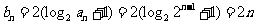
则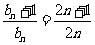 ,所以
,所以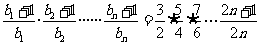 .
. 

下面用数学归纳法证明不等式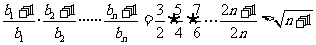 成立.
成立.
① 当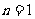 时,左边=
时,左边=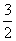 ,右边=
,右边=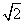 ,因为
,因为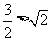 ,所以不等式成立.
,所以不等式成立.
② 假设当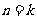 时不等式成立,即
时不等式成立,即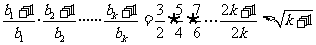 成立.则当
成立.则当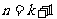 时,左边=
时,左边=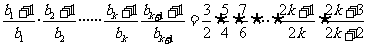

所以当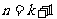 时,不等式也成立. .
时,不等式也成立. . 

由①、②可得不等式恒成立.
[命题立意]:本题主要考查了等比数列的定义,通项公式,以及已知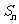 求
求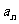 的基本题型,并运用数学归纳法证明与自然数有关的命题,以及放缩法证明不等式.
的基本题型,并运用数学归纳法证明与自然数有关的命题,以及放缩法证明不等式.
21.(2009江苏卷)(本题满分10分)
对于正整数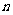 ≥2,用
≥2,用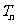 表示关于
表示关于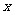 的一元二次方程
的一元二次方程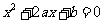 有实数根的有序数组
有实数根的有序数组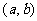 的组数,其中
的组数,其中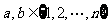 (
(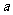 和
和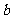 可以相等);对于随机选取的
可以相等);对于随机选取的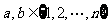 (
(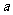 和
和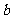 可以相等),记
可以相等),记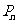 为关于
为关于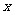 的一元二次方程
的一元二次方程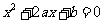 有实数根的概率。
有实数根的概率。
(1)求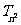 和
和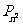 ;
;
(2)求证:对任意正整数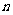 ≥2,有
≥2,有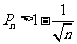 .
.
[解析] [必做题]本小题主要考查概率的基本知识和记数原理,考查探究能力。满分10分。
 .
.


20.(2009江苏卷)(本小题满分14分)
设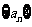 是公差不为零的等差数列,
是公差不为零的等差数列,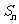 为其前
为其前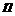 项和,满足
项和,满足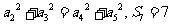 。
。
(1)求数列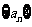 的通项公式及前
的通项公式及前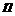 项和
项和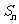 ;
;

(2)试求所有的正整数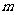 ,使得
,使得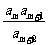 为数列
为数列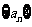 中的项。
中的项。

[解析] 本小题主要考查等差数列的通项、求和的有关知识,考查运算和求解的能力。满分14分。
(1)设公差为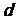 ,则
,则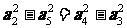 ,由性质得
,由性质得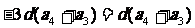 ,因为
,因为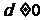 ,所以
,所以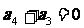 ,即
,即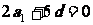 ,又由
,又由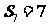 得
得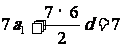 ,解得
,解得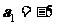 ,
,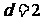 ,
,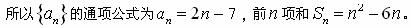
(2) (方法一)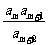 =
=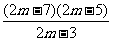 ,设
,设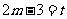 ,
,

则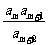 =
=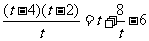 , 所以
, 所以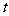 为8的约数
为8的约数

(方法二)因为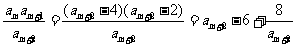 为数列
为数列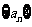 中的项,
中的项,
故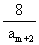 为整数,又由(1)知:
为整数,又由(1)知: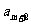 为奇数,所以
为奇数,所以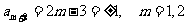
经检验,符合题意的正整数只有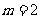 。.
。. 

19.(2009浙江文)(本题满分14分)设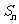 为数列
为数列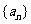 的前
的前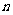 项和,
项和,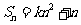 ,
,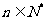 ,其中
,其中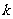 是常数.
是常数.
(I) 求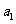 及
及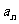 ;
;
(II)若对于任意的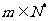 ,
,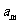 ,
,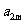 ,
,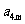 成等比数列,求
成等比数列,求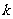 的值.
的值.
解析:(Ⅰ)当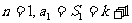 ,
,
 (
( )
)
经验,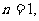 (
( )式成立,
)式成立, 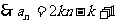
(Ⅱ)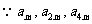 成等比数列,
成等比数列,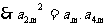 ,
,
即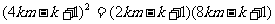 ,整理得:
,整理得: ,
,
对任意的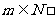 成立,
成立,
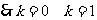
18.(2009年广东卷文)(本小题满分14分)
已知点(1,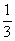 )是函数
)是函数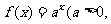 且
且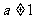 )的图象上一点,等比数列
)的图象上一点,等比数列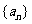 的前
的前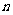 项和为
项和为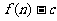 ,数列
,数列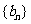
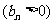 的首项为
的首项为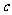 ,且前
,且前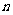 项和
项和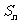 满足
满足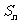 -
-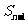 =
=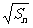 +
+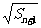 (
(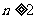 ).
).
(1)求数列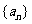 和
和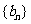 的通项公式;
的通项公式;
(2)若数列{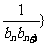 前
前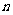 项和为
项和为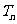 ,问
,问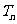 >
>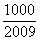 的最小正整数
的最小正整数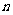 是多少? .
是多少? . 

[解析](1)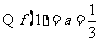 ,
,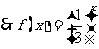
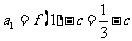 ,
,
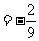 ,
,
 .
.
又数列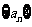 成等比数列,
成等比数列,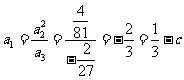 ,所以
,所以 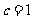 ;
;
又公比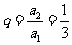 ,所以
,所以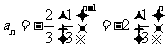
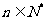 ;
;
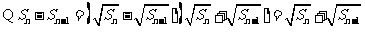
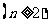
又 ,
,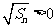 ,
,
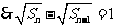 ;
;
数列 构成一个首相为1公差为1的等差数列,
构成一个首相为1公差为1的等差数列,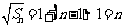 ,
, 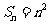
当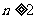 ,
, 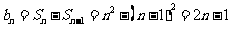 ;
;
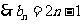 (
(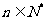 );
);
(2)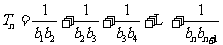
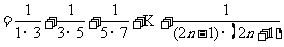
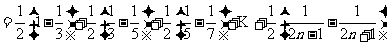
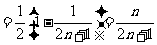 ;
;
由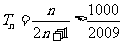 得
得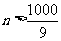 ,满足
,满足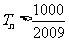 的最小正整数为112.
的最小正整数为112.
17.(2009宁夏海南卷文)等比数列{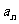 }的公比
}的公比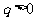 , 已知
, 已知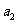 =1,
=1,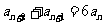 ,则{
,则{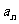 }的前4项和
}的前4项和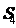 = .
= . 

[答案]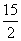
[解析]由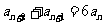 得:
得: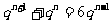 ,即
,即 ,
,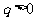 ,解得:q=2,又
,解得:q=2,又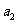 =1,所以,
=1,所以,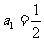 ,
,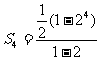 =
=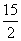 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com