
3、(2010·哈尔滨模拟)设反应① △H=akJ/mol,反应
△H=akJ/mol,反应
②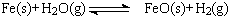 △H=bkJ/mol,以上两反应的平衡常数分别为K1和K2。在不同温度下,K1、K2的值如下:
△H=bkJ/mol,以上两反应的平衡常数分别为K1和K2。在不同温度下,K1、K2的值如下:
|
T/K |
K1 |
K2 |
|
973 |
1.47 |
2.38 |
|
1173 |
2.15 |
1.67 |
下列有关叙述正确的是( )
A.b>0 B.在973K下增大压强,K2增大
C.a>b D.在常温下反应①一定能自发进行
[解析]选C。平衡常数只与温度有关,温度不变时,增大压强,K2不变;对于反应①能否自发进行,要看△H- T△S的值。
2、(2010·南京模拟)在500℃,恒容的密闭容器中合成氨,起始充入氮气和氢气共a mol,平衡时容器内压强为起始时的75%;若起始充入氮气、氢气和氨气的混合气体共a mol,测得平衡时压强仍为起始时的75%,则两次平衡体系中氨气的百分含量的关系是( )
A.前者 > 后者 B.前者 < 后者 C.两者相等 D.无法确定
[解析]选B。起始充入氮气、氢气和氨气的混合气体共a mol,相当于充入氮气、氢气的物质的量的和多于a mol,合成氨反应正向气体化学计量数减少,而两种情况平衡时压强相同,所以,后者相当于平衡正向移动,氨气的百分含量后者大。
1、(2010·济南模拟)在一恒容密闭容器中通入A、B两种气体,在一定条件下发生反应:
2A(g)+B(g)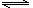 2C(g);△H<0。当达到平衡后,保持其他条件不变,只改变条件X,则相应量Y的改变一定符合图中曲线的是( )
2C(g);△H<0。当达到平衡后,保持其他条件不变,只改变条件X,则相应量Y的改变一定符合图中曲线的是( )
|
|
X |
Y |
|
A |
温度 |
C的体积分数 |
|
B |
充入稀有气体 |
A的物质的量 |
|
C |
再加入A |
B的转化率 |
|
D |
再加入C |
A的百分含量 |
[解析]选C。A项,该反应是放热反应,温度升高时化学平衡逆向移动,C的体积分数下降,与图不符合;B项,恒容密闭容器中充入稀有气体,平衡不移动,A的物质的量不变,不符合;C项,再加入A,平衡正向移动,B的转化率增大,符合;D项,再加入C,相当于压强增大,平衡正向移动,A的百分含量减少。
1 ?球O1、O2、分别与正方体的各面、各条棱相切,正方体的各顶点都在球O3的表面上,求三个球的表面积之比.
?球O1、O2、分别与正方体的各面、各条棱相切,正方体的各顶点都在球O3的表面上,求三个球的表面积之比.
分析:球的表面积之比事实上就是半径之比的平方,故只需找到球半径之间的关系即可.
解:设正方体棱长为a,则三个球的半径依次为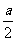 、
、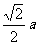 ,
,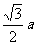
∴ 三个球的表面积之比是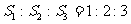 .
.
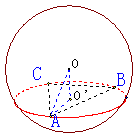
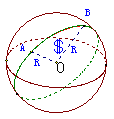
例1  已知过球面上
已知过球面上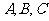 三点的截面和球心的距离为球半径的一半,且
三点的截面和球心的距离为球半径的一半,且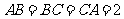 ,求球的表面积
,求球的表面积
解:设截面圆心为 ,连结
,连结 ,设球半径为
,设球半径为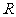 ,
,
 则
则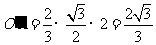 ,
,
在 中,
中, ,
,
∴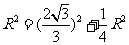 ,∴
,∴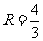 ,
,
∴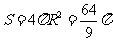 .
.
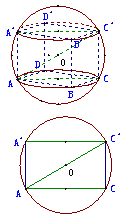
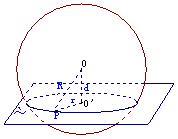
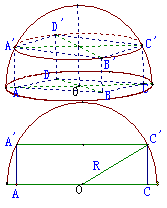 例2.半球内有一个内接正方体,正方体的一个面在半球的底面圆内,若正方体棱长为
例2.半球内有一个内接正方体,正方体的一个面在半球的底面圆内,若正方体棱长为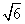 ,求球的表面积和体积
,求球的表面积和体积
解:作轴截面如图所示,
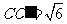 ,
,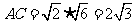 ,
,
设球半径为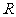 ,
,
则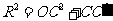
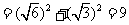
∴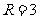 ,
,
 ∴
∴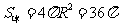 ,
,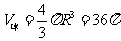 .
.
例3.表面积为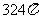 的球,其内接正四棱柱的高是
的球,其内接正四棱柱的高是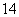 ,求这个正四棱柱的表面积
,求这个正四棱柱的表面积
解:设球半径为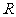 ,正四棱柱底面边长为
,正四棱柱底面边长为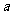 ,
,
则作轴截面如图, ,
,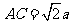 ,
,
又∵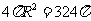 ,∴
,∴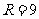 ,
,
∴ ,∴
,∴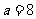 ,
,
∴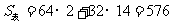 .
.
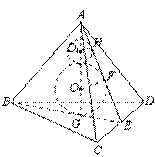
例4 正四面体ABCD的棱长为a,球O是内切球,球O1是与正四面体的三个面和球O都相切的一个小球,求球O1的体积.
分析:正四面体的内切球与各面的切点是面的中心,球心到各面的距离相等.
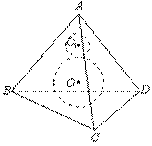 解:如图,设球O半径为R,球O1的半径为r,E为CD中点,球O与平面ACD、BCD切于点F、G,球O1与平面ACD切于点H.
解:如图,设球O半径为R,球O1的半径为r,E为CD中点,球O与平面ACD、BCD切于点F、G,球O1与平面ACD切于点H.
由题设
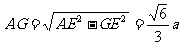 .
.
∵ △AOF∽△AEG ∴ 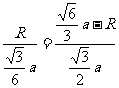 ,得
,得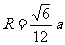 .
.
 ∵ △AO1H∽△AOF ∴
∵ △AO1H∽△AOF ∴ 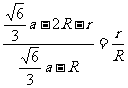 ,得
,得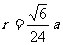 .
.
∴ 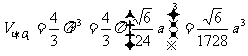 .
.
1  球的表面积:
球的表面积:
设球 的半径为
的半径为 ,我们把球面任意分割为一些“小球面片”,它们的面积分别用
,我们把球面任意分割为一些“小球面片”,它们的面积分别用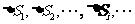 表示,则球的表面积:
表示,则球的表面积:
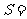
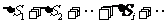
以这些“小球面片”为底,球心为顶点的“小锥体”的体积和等于求的体积,这些“小锥体”可近似地看成棱锥,“小锥体”的底面积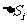 可近似地等于“小锥体”的底面积,球的半径
可近似地等于“小锥体”的底面积,球的半径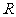 近似地等于小棱锥的高
近似地等于小棱锥的高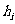 ,因此,第
,因此,第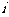 个小棱锥的体积
个小棱锥的体积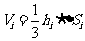 ,当“小锥体”的底面非常小时,“小锥体”的底面几乎是“平的”,于是球的体积:
,当“小锥体”的底面非常小时,“小锥体”的底面几乎是“平的”,于是球的体积:

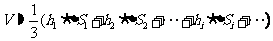 ,
,
又∵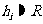 ,且
,且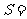
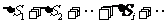
∴可得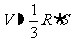 ,
,
又∵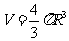 ,∴
,∴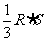
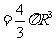 ,
,
∴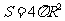 即为球的表面积公式
即为球的表面积公式
6.球的体积公式: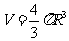

4.两点的球面距离:
球面上两点之间的最短距离,就是经过两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离
5  半球的底面:
半球的底面:
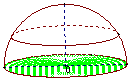 已知半径为
已知半径为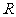 的球
的球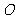 ,用过球心的平面去截球
,用过球心的平面去截球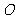 ,球被截面分成大小相等的两个半球,截面圆
,球被截面分成大小相等的两个半球,截面圆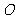 (包含它内部的点),叫做所得半球的底面
(包含它内部的点),叫做所得半球的底面
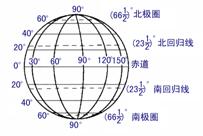
3.经度、纬度:
经线:球面上从北极到南极的半个大圆;
纬线:与赤道平面平行的平面截球面所得的小圆;
经度:某地的经度就是经过这点的经线与地轴确定的半平面与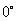 经线及轴确定的半平面所成的二面角的度数;
经线及轴确定的半平面所成的二面角的度数;
纬度:某地的纬度就是指过这点的球半径与赤道平面所成角的度数

与定点距离等于或小于定长的点的集合,叫做球体,简称球 定点叫球心,定长叫球的半径
定点叫球心,定长叫球的半径 与定点距离等于定长的点的集合叫做球面
与定点距离等于定长的点的集合叫做球面 一个球或球面用表示它的球心的字母表示,例如球
一个球或球面用表示它的球心的字母表示,例如球 .
.
2.球的截面:
 用一平面
用一平面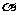 去截一个球
去截一个球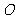 ,设
,设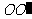 是平面
是平面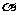 的垂线段,
的垂线段, 为垂足,且
为垂足,且 ,所得的截面是以球心在截面内的射影为圆心,以
,所得的截面是以球心在截面内的射影为圆心,以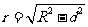 为半径的一个圆,截面是一个圆面
为半径的一个圆,截面是一个圆面
球面被经过球心的平面截得的圆叫做大圆,被不经过球心的平面截得的圆叫做小圆
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com