
6.人类的多指是一种显性遗传病,白化病是一种隐性遗传病,已知控制这两种疾病的等位基因都是独立遗传的。在一个家庭中,父亲是多指,母亲正常,他们有一个患白化病但手指正常的孩子,则下一个孩子正常或同时患有此两种疾病的机率分别是
A.3/4,1/4 B.3/8,1/8 C.1/4,l/4 D.1/4,l/8
5.假如水稻高秆(D)对矮秆(d)为显性,抗稻瘟病(R)对易感稻瘟病(r)为显性,两对性状独立遗传。用一个纯合易感病的矮秆品种(抗倒伏)与一个纯合抗病高秆品种(易倒伏)杂交,F2代中出现既抗病又抗倒伏类型的基因型及其比例为
A.ddRR 1/8 B.ddRr 1/16
C.ddRR 1/16 和ddRr 1/8 D.DDRr 1/16 和DdRR 1/8
4.已知黑尿症是由隐性基因控制的,丈夫的哥哥和妻子的妹妹都是黑尿症患者,夫妻双方的其他家族成员均正常。表现正常的该夫妇生育出黑尿症患儿的概率是
A.1/9 B.1/8 C.1/4 D.1/3
3.下列各组中,属于相对性状的是
A.双眼皮与大眼睛 B.身高与体重 C.狗的短毛与长毛 D.羊的卷毛与长毛
2.下面是对基因型与表现型关系的叙述,其中错误的是
A.表现型相同,基因型不一定相同
B.基因型相同,表现型也不一定相同
C.若环境相同,则基因型相同的个体表现型相同
D.在同样的环境中,表现型相同的个体基因型必定相同
1.在植物杂交育种实验中,将纸袋套在花上是为了
A.给花保温 B.防止花粉被风吹走 C.防止自花授粉 D.防止外来花粉干扰
14.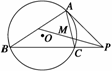 已知:如图所示,△ABC内接于⊙O,过点A的切线交BC
已知:如图所示,△ABC内接于⊙O,过点A的切线交BC
的延长线于点P,D为AB的中点,DP交AC于M.
求证: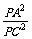 =
=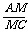 .
.
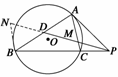 证明 如图所示,过点B作BN∥CM,交PD的延长线于点N,
证明 如图所示,过点B作BN∥CM,交PD的延长线于点N,
则∠N=∠AMD,∠NBD=∠DAM.
又AD=DB,∴△BND≌△AMD.∴BN=AM.
∵CM∥BN,∴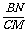 =
=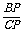 .
.
∴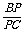 =
=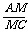 .
.
由切割线定理,得PA2=PC·PB.
∴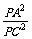 =
=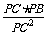 =
=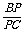 ,故
,故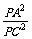 =
=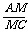 .
.
13.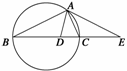 (2008·江苏)如图所示,设△ABC的外接圆的切线
(2008·江苏)如图所示,设△ABC的外接圆的切线
AE与BC的延长线交于点E,∠BAC的平分线与BC交
于点D.
求证:ED2=EC·EB.
证明 如图所示,因为AE是圆的切线,
所以∠ABC=∠CAE.
又因为AD是∠BAC的平分线,所以∠BAD=∠CAD.
从而∠ABC+∠BAD=∠CAE+∠CAD.
因为∠ADE=∠ABC+∠BAD,
∠DAE=∠CAE+∠CAD,
所以∠ADE=∠DAE,故EA=ED.
因为EA是圆的切线,所以由切割线定理知,
EA2=EC·EB,
而EA=ED,所以ED2=EC·EB.
12.(2008·宁夏)如图所示,过圆O外一点M作它的一条切线,切点为A,过A点作直线AP垂直于直线OM,垂足为P.
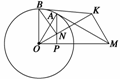
(1)证明:OM·OP=OA2;
(2)N为线段AP上一点,直线NB垂直于直线ON,且交圆O于B点.过B点的切线交直线ON于K.
证明:∠OKM=90°.
证明 (1)因为MA是圆O的切线,所以OA⊥AM.
又因为AP⊥OM,在Rt△OAM中,由射影定理知,
OA2=OM·OP.
(2)因为BK是圆O的切线,BN⊥OK,
同(1),有OB2=ON·OK,又OB=OA,
所以OP·OM=ON·OK,即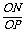 =
=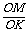 .
.
又∠NOP=∠MOK,
所以△ONP∽△OMK,故∠OKM=∠OPN=90°.
11.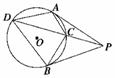 (2008·苏南四市二检) 从⊙O外一点P引圆的两条切
(2008·苏南四市二检) 从⊙O外一点P引圆的两条切
线PA,PB及一条割线PCD,A,B为切点.
求证: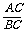 =
=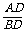 .
.
证明 ∵PA为⊙O的切线,∴∠PAC=∠PDA,
而∠APC=∠DPA,∴△PAC∽△PDA,
则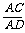 =
=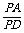 .同理
.同理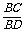 =
=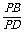 .
.
∵PA=PB,∴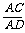 =
=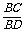 .∴
.∴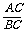 =
=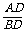 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com