
2.匀加速直线运动
1.定义:在变速直线运动中,如果在相等的时间内速度的改变相等,这种运动称为匀变速直线运动。
24、(本小题满分10分)选修4-5,不等式选讲设函数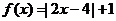
(Ⅰ)画出函数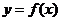 的图像
的图像
(Ⅱ)若不等式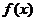 ≤ax的解集非空,求a的取值范围。
≤ax的解集非空,求a的取值范围。
解:
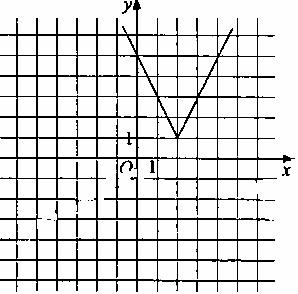 (Ⅰ)由于
(Ⅰ)由于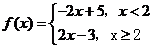 则函数
则函数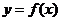 的图像如图所示。
的图像如图所示。
(Ⅱ)由函数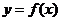 与函数
与函数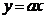 的图像可知,当且仅当
的图像可知,当且仅当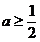 或
或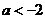 时,函数
时,函数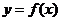 与函数
与函数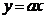 的图像有交点。故不等式
的图像有交点。故不等式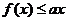 的解集非空时,
的解集非空时,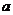 的取值范围为
的取值范围为
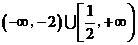 。
。
高.考.资.源.网
高☆考♂资♀源?网
|

|
版权所有:()
23、(本小题满分10分)选修4-4:坐标系与参数方程。
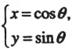
已知P为半圆C:
(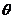 为参数,
为参数,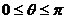 )上的点,点A的坐标为(1,0),
)上的点,点A的坐标为(1,0),
O为坐标原点,点M在射线OP上,线段OM与C的弧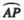 的长度均为
的长度均为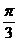 。
。
(I)以O为极点, x轴的正半轴为极轴建立极坐标系,求点M的极坐标;
(II)求直线AM的参数方程。

(Ⅱ)M点的直角坐标为(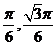 ),A(0,1),故直线AM的参数方程为
),A(0,1),故直线AM的参数方程为
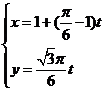 (t为参数)
……10分
(t为参数)
……10分
22、(本小题满分10分)选修4-1:几何证明选讲如图,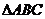 的角平分线AD的延长线交它的外接圆于点E.
的角平分线AD的延长线交它的外接圆于点E.
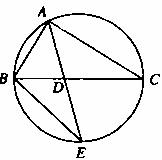 (I)证明:
(I)证明: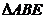
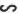
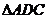
(II)若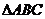 的面积
的面积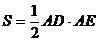 ,求
,求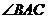 的大小。
的大小。
(Ⅰ)由已知条件,可得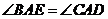
因为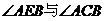 是同弧上的圆周角,
是同弧上的圆周角,
所以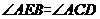
故△ABE∽△ADC. ……5分
(Ⅱ)因为△ABE∽△ADC,所以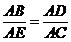 ,即AB·AC=AD·AE.
,即AB·AC=AD·AE.
又S=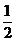 AB·ACsin
AB·ACsin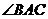 ,且S=
,且S=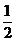 AD·AE,故AB·ACsin
AD·AE,故AB·ACsin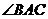 = AD·AE.
= AD·AE.
则sin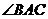 =1,又
=1,又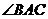 为三角形内角,所以
为三角形内角,所以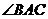 =90°.
……10分
=90°.
……10分
21、(本小题12分)设函数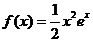 .
.
(1)求函数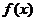 的单调区间;
的单调区间;
(2)若当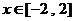 时,不等式恒
时,不等式恒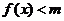 成立,求实数m的取值范围.
成立,求实数m的取值范围.
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所作的第一题记分。作答时先写清楚所选题目的题号。
[解](1)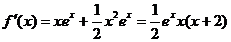 ,
,
令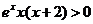 ,得
,得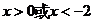 ,
,
∴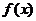 的增区间为
的增区间为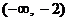 和
和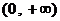 ,………3分
,………3分
令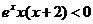 ,得
,得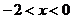 ,
,
 ∴
∴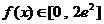 ,
……………………………………………………………11分
,
……………………………………………………………11分
∴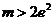 .
………………………………………………………………………12分
.
………………………………………………………………………12分
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所作的第一题记分。作答时先写清楚所选题目的题号。
19、(本小题12分)已知函数f ( x ) =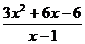 。
。
(Ⅰ)求函数f ( x
)在点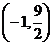 处的切线方程;
处的切线方程;
(Ⅱ)求函数f ( x )的极大值和极小值。

况如下表:
|
x |
(-∞,0) |
0 |
( 0 , 1 ) ,
(1 , 2 ) |
2 |
( 2 , +∞ ) |
|
f′( x ) |
+ |
0 |
– |
0 |
+ |
………… 9分
所以当x = 0时,函数f ( x )取得极大值为6;当x = 2时,函数f ( x )取得极小值为18。
………… 12分
18、(本小题12分)
已知集合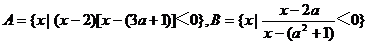 ,其中a≠1
,其中a≠1
(1)当a=2时,求A∩B; (2)求使B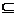 A的实数a的取值范围。
A的实数a的取值范围。
解析:(1)当a=2时,A=(2,7),B=(4,5)
∴A∩B=(4,5) ················4分
(2)∵B=(2a,a2+1)
当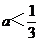 时,A=(3a+1,2)要使
时,A=(3a+1,2)要使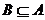 ,必须
,必须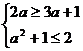 ,此时a=-1; ···6分
,此时a=-1; ···6分
当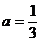 时,
时, ,使
,使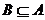 的a不存在; ···8分
的a不存在; ···8分
当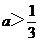 时,A=(2,3a+1)要使
时,A=(2,3a+1)要使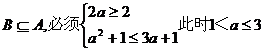
综上可知,使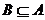 ,的实数a的取值范围
,的实数a的取值范围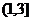 ················12分
················12分
17、(本小题12分)
已知函数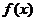 对一切
对一切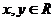 都有
都有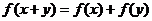
(1)试判断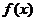 的奇偶性;
的奇偶性;
(2)若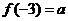 ,用
,用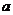 表示
表示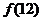 .
.
的最大
奇;-4a
16、对于函数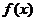 ,在使
,在使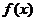 ≥M恒成立的所有常数M中,我们把M中的最大值称为函数
≥M恒成立的所有常数M中,我们把M中的最大值称为函数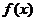 的“下确界”,则函数
的“下确界”,则函数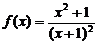 的下确界为 0.5 .
的下确界为 0.5 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com