
15.
(2008 河南实验区)已知
 是关于
是关于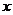 的一元二次方程
的一元二次方程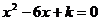 的两个实数根,且
的两个实数根,且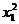
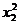 -
-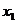 -
- =115
=115
(1)求k的值;(2)求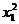 +
+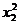 +8的值。
+8的值。
14.
(2008 广东)(1)解方程求出两个解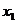 、
、 ,并计算两个解的和与积,填人下表
,并计算两个解的和与积,填人下表
|
方程 |
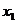 |
 |
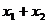 |
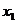 . . |
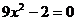 |
|
|
|
|
 |
|
|
|
|
 |
|
|
|
|
关于x的方程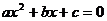 ( 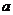 、 、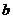 、 、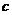 为常数, 为常数,且 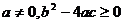 ) ) |
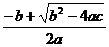 |
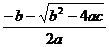 |
|
|
(2)观察表格中方程两个解的和、两个解的积与原方程的系数之间的关系有什么规律?写出你的结论.
13.(2008泰安) 用配方法解方程: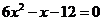 .
.
12.(08厦门市)某商店购进一种商品,单价30元.试销中发现这种商品每天的销售量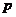 (件)与每件的销售价
(件)与每件的销售价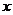 (元)满足关系:
(元)满足关系: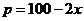 .若商店每天销售这种商品要获得200元的利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
.若商店每天销售这种商品要获得200元的利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
11.(2008北京)已知:关于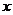 的一元二次方程
的一元二次方程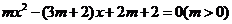 .
.
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为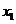 ,
,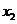 (其中
(其中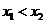 ).若
).若 是关于
是关于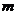 的函数,且
的函数,且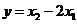 ,求这个函数的解析式;
,求这个函数的解析式;
(3)在(2)的条件下,结合函数的图象回答:当自变量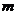 的取值范围满足什么条件时,
的取值范围满足什么条件时,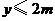 .
.
10.(2008湖北鄂州)设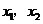 是关于
是关于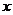 的一元二次方程
的一元二次方程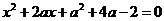 的两实根,当
的两实根,当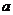 为何值时,
为何值时,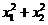 有最小值?最小值是多少?
有最小值?最小值是多少?
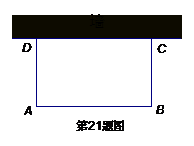
9.(2008江苏南京)某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿前侧的侧内墙保留3m宽的空地.其它三侧内墙各保留1m宽的通道,当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?
8. (2008 湖北 十堰)如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
⑴怎样围才能使矩形场地的面积为750m2?
⑵能否使所围矩形场地的面积为810m2,为什么?
7.(2008
湖南 长沙)当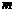 为何值时,关于
为何值时,关于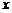 的一元二次方程
的一元二次方程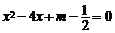 有两个相等的实数根?此时这两个实数根是多少?
有两个相等的实数根?此时这两个实数根是多少?
6.(2008 重庆)解方程: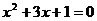
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com