
3.基本方法
(1)编写一个程序的三个步骤:
第一步:算法分析:根据提供的问题,利用数学及相关学科的知识,设计出解决问题的算法;
第二步:画出程序框图:依据算法分析,画出对应的程序框图;
第三步:写出程序:耕具程序框图中的算法步骤,逐步把算法用相应的程序语句表达出来.
(2)何时应用条件结构?
当问题设计到一些判断,进行分类或分情况,或者比较大小时,应用条件结构;分成三种类型以上(包括三种)时,由边界开始逐一分类,应用多重条件结构.注意条件的边界值.
(3)何时应用循环结构?
当反复执行某一步骤或过程时,应用循环结构.当型循环是先判断条件,条件满足再执行循环体,不满足退出循环;直到型循环是先执行循环体,再判断条件,不满足条件时执行循环体,满足时退出循环.
应用循环结构前:①确定循环变量和初始条件;②确定算法中反复执行的部分,即循环体;③确定循环的终止条件.
2.三种基本逻辑结构
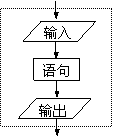
(1)顺序结构
顺序结构是由若干个依次执行的处理步骤组成.
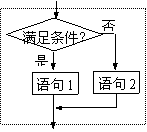
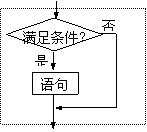
(2)选择结构
根据条件判断,决定不同流向.
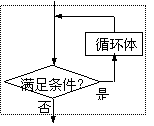
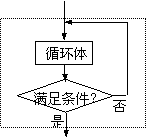
(3)循环结构
从某处开始,按照一定条件,反复执行某一处理步骤.
(1)当型(WHILE型)循环;
(2)直到型(UNTIL型)循环;
1.算法的基本概念
(1)算法定义描述:在数学中,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.
(2)算法的特性:
①有穷性:一个算法的步骤序列是有限的,它应在有限步操作之后停止,而不能是无限的.
②确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可.
③可行性:算法中的每一步操作都必须是可执行的,也就是说算法中的每一步都能通过手工和机器在有限时间内完成.
④输入:一个算法中有零个或多个输入..
⑤输出:一个算法中有一个或多个输出.
4.框图属于新增内容,将以考察考生的实际应用能力为主,考查考生的知识迁移能力.
3.高考对于复数的考察主要以复数的四则运算为主,按新课标的要求高考将不再考察共轭复数、复数的模等知识点;
2.推理证明题主要和其它知识结合到一块,属于知识综合题,解决此类题目时要建立合理的解题思路;
1.简易逻辑的重点内容是有关“充要条件”、命题真伪的试题。主要是对数学概念有准确的记忆和深层次的理解,试题以选择题、填空题为主,难度不大,要求对基本知识、基本题型,求解准确熟练;
题型1:判断命题的真值
例1.写出由下述各命题构成的“p或q”,“p且q”,“非p”形式的复合命题,并指出所构成的这些复合命题的真假.
(1)p:9是144的约数,q:9是225的约数。
(2)p:方程x2-1=0的解是x=1,q:方程x2-1=0的解是x=-1;
(3)p:实数的平方是正数,q:实数的平方是0.
解析:由简单命题构成复合命题,一定要检验是否符合“真值表”如果不符要作语言上的调整。
(1)p或q:9是144或225的约数;
p且q:9是144与225的公约数,(或写成:9是144的约数,且9是225的约数);
非p:9不是144的约数.
∵p真,q真,∴“p或q”为真,“p且q” 为真,而“非p”为假.
(2)p或q:方程x2-1=0的解是x=1,或方程x2-1=0的解是x=-1(注意,不能写成“方程x2-1=0的解是x=±1”,这与真值表不符);
p且q:方程x2-1=0的解是x=1,且方程x2-1=0的解是x=-1;
非p:方程x2-1=0的解不都是x=1(注意,在命题p中的“是”应理解为“都是”的意思);
∵p假,q假,∴“p或q”与,“p且q” 均为假,而“非p”为真.
(3)p或q:实数的平方都是正数或实数的平方都是0;
p且q:实数的平方都是正数且实数的平方都是0;
非p:实数的平方不都是正数,(或:存在实数,其平方不是正数);
∵p假,q假,∴“p或q”与“p且q” 均为假,而“非p”为真.
点评:在命题p或命题q的语句中,由于中文表达的习惯常常会有些省略,这种情况下应作词语上的调整。
题型2:条件
例2.(1) “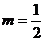 ”是“直线
”是“直线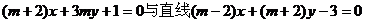 相互垂直”的( )
相互垂直”的( )
A.充分必要条件 B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
答案:B;
解析:当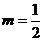 时两直线斜率乘积为
时两直线斜率乘积为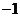 从而可得两直线垂直,当
从而可得两直线垂直,当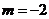 时两直线一条斜率为0一条斜率不存在,但两直线仍然垂直.因此
时两直线一条斜率为0一条斜率不存在,但两直线仍然垂直.因此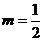 是题目中给出的两条直线垂直的充分但不必要条件。
是题目中给出的两条直线垂直的充分但不必要条件。
点评:对于两条直线垂直的充要条件①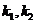 都存在时
都存在时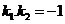 ②
②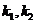 中有一个不存在另一个为零对于②这种情况多数考生容易忽略。
中有一个不存在另一个为零对于②这种情况多数考生容易忽略。
(2)设集合A={x|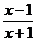 <0
<0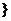 ,B={x || x -1|<a
,B={x || x -1|<a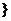 ,若“a=1”是“A∩B≠
,若“a=1”是“A∩B≠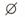 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
答案:A;
解析:由题意得A:-1<x<1,B:1-a<x<a+1,
1)由a=1。A:-1<x<1.B:0<x<2。
则A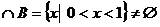 成立,即充分性成立。
成立,即充分性成立。
2)反之:A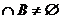 ,不一定推得a=1,如a可能为
,不一定推得a=1,如a可能为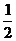 。
。
综合得“a=1”是:
A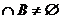 ”的充分非必要条件,故选A。
”的充分非必要条件,故选A。
点评:本题考查分式不等式,绝对值不等式的解法,充分必要条件等知识。
题型3:四种命题
例3.(1)(2009宁夏海南卷理)复数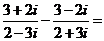 ( )
( )
(A)0 (B)2 (C)-2i (D)2
[解析]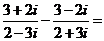
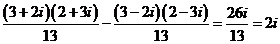 ,选D
,选D
答案 D
(2)很可能许多同学会认为它是假命题(原因m=0时显然方程有根),而它的逆否命题:“若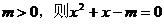 有实根”,显然为真,其实不然,由
有实根”,显然为真,其实不然,由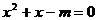 没实根可推得
没实根可推得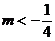 ,而
,而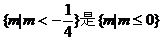 的真子集,由
的真子集,由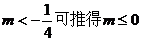 ,故原命题为真,其实,用逆否命题很容易判断它是真命题;
,故原命题为真,其实,用逆否命题很容易判断它是真命题;
点评:本题考查了命题间的关系,由原命题写出其否命题。
题型4:全称命题与特称命题
例4.命题p:“有些三角形是等腰三角形”,则┐p是( )
A.有些三角形不是等腰三角形
B.所有三角形是等腰三角形
C.所有三角形不是等腰三角形
D.所有三角形是等腰三角形
解析:像这种存在性命题的否定命题也有其规律:命题p:“存在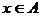 使P(x)成立”,┐p为:“对任意
使P(x)成立”,┐p为:“对任意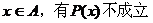 ”,它恰与全称性命题的否定命题相反,故的答案为C。
”,它恰与全称性命题的否定命题相反,故的答案为C。
点评:简易逻辑题,比较抽象,不少学生在有些问题的看法上常出现一些自己也说不清道不明的疑惑,但要依据具体的规则进行详细的处理。
题型5:合情推理
例5.(1)观察圆周上n个点之间所连的弦,发现两个点可以连一条弦,3个点可以连3条弦,4个点可以连6条弦,5个点可以连10条弦,你由此可以归纳出什么规律?
(2)把下面在平面内成立的结论类比推广到空间,并判断类比的结论是否成立:
1)如果一条直线与两条平行直线中的一条相交,则必于另一条相交。
2)如果两条直线同时垂直与第三条直线,则这两条直线平行。
解析:(1)设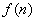 为
为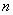 个点可连的弦的条数,则
个点可连的弦的条数,则
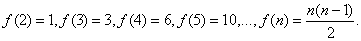
(2)
1)一个平面如和两个平行平面中的一个相交,则必然和另一个也相交,次结论成立;
2)若两个平面同时垂直第三个骗马,则这两个平面也相互平行,此结论不成立。
点评:当前提为真,结论可能为真的推理。一定要理解合情推理的必要性。
题型6:演绎推理
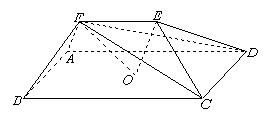 例6.(07年天津)如图,在五面体
例6.(07年天津)如图,在五面体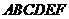 中,点
中,点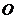 是矩形
是矩形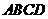 的对角线的交点,面
的对角线的交点,面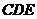 是等边三角形,棱
是等边三角形,棱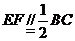 。
。
(1)证明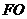 //平面
//平面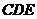 ;
;
(2)设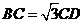 ,证明
,证明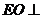 平面
平面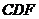 。
。
解析:(Ⅰ)证明:取CD中点M,连结OM.
在矩形ABCD中,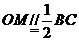 ,又
,又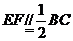 ,
,
则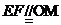 ,连结EM,于是四边形EFOM为平行四边形.
,连结EM,于是四边形EFOM为平行四边形.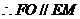
又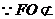 平面CDE,切EM
平面CDE,切EM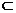 平面CDE,∵FO∥平面CDE
平面CDE,∵FO∥平面CDE
(Ⅱ)证明:连结FM,由(Ⅰ)和已知条件,在等边△CDE中,
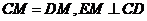 且
且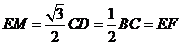 。
。
因此平行四边形EFOM为菱形,从而EO⊥FM而FM∩CD=M,∴CD⊥平面EOM,从而CD⊥EO.而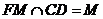 ,所以EO⊥平面CDF。
,所以EO⊥平面CDF。
点评:本小题考查直线与平面平行、直线与平面垂直等基础知识,考查空间想象能力和推理论证能力.
题型7:特殊证法
例7.(1)用反证法证明:如果a>b>0,那么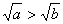 ;
;
(2)(全国II)设数列{an}的前n项和为Sn,且方程x2-anx-an=0有一根为Sn-1,n=1,2,3,…。
(Ⅰ)求a1,a2;(Ⅱ){an}的通项公式。
解析:(1)假设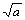 不大于
不大于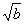 ,则或者
,则或者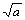 <
<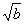 ,或者
,或者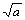 =
=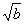 。
。
∵a>0,b>0,∴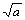 <
<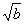
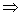
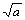
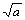 <
<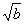
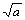 ,
,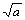
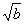 <
<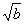
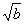
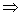
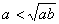 ,
,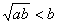
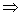 a<b;
a<b;
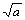 =
=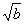
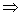 a=b.这些都同已知条件a>b>0矛盾,∴
a=b.这些都同已知条件a>b>0矛盾,∴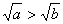 .
.
证法二(直接证法)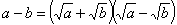 ,
,
∵a>b>0,∴a - b>0即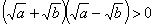 ,
,
∴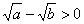 ,∴
,∴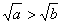 。
。
(2)(Ⅰ)当n=1时,x2-a1x-a1=0有一根为S1-1=a1-1,
于是(a1-1)2-a1(a1-1)-a1=0,解得a1=。
当n=2时,x2-a2x-a2=0有一根为S2-1=a2-,
于是(a2-)2-a2(a2-)-a2=0,解得a1=。
(Ⅱ)由题设(Sn-1)2-an(Sn-1)-an=0,Sn2-2Sn+1-anSn=0。
当n≥2时,an=Sn-Sn-1,代入上式得Sn-1Sn-2Sn+1=0 ①
由(Ⅰ)知S1=a1=,S2=a1+a2=+=。
由①可得S3=,由此猜想Sn=,n=1,2,3,…
下面用数学归纳法证明这个结论
(i)n=1时已知结论成立;
(ii)假设n=k时结论成立,即Sk=,
当n=k+1时,由①得Sk+1=,即Sk+1=,
故n=k+1时结论也成立.
综上,由(i)、(ii)可知Sn=对所有正整数n都成立,
于是当n≥2时,an=Sn-Sn-1=-=,
又n=1时,a1==,所以{an}的通项公式an=,n=1,2,3,…
点评:要应用好反证法、数学归纳法证明一些涉及代数、不等式、几何的结论。
题型8:复数的概念及性质
例8.(1(沈阳二中2009届高三期末数学试题)如果复数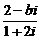 (其中
(其中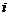 为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于 ( )
为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于 ( )
A.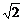 B.
B.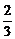 C.
C.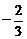 D.2
D.2
答案 C
(2)(2009北京卷理)在复平面内,复数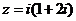 对应的点位于
( )
对应的点位于
( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
[解析] ∵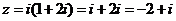 ,∴复数
,∴复数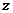 所对应的点为
所对应的点为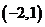 ,故选B.
,故选B.
答案 B
点评:复数的概念和性质是高考对复数部分的一个考点,属于比较基本的题目,主要考察复数的的分类和几何性质.
题型9:复数的运算
例9.(1)
(浙江卷)已知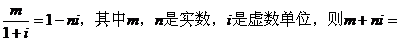 ( )
( )
(A)1+2i (B) 1-2i (C)2+i (D)2-i
(2)(湖北卷)设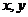 为实数,且
为实数,且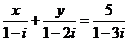 ,则
,则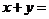 。
。
解析:(1)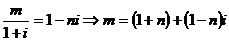 ,由
,由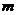 、
、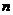 是实数,得
是实数,得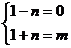 ,
,
∴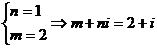 ,故选择C。
,故选择C。
(2)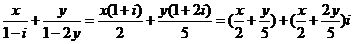 ,
,
而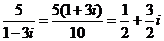 所以
所以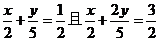 ,解得x=-1,y=5,
,解得x=-1,y=5,
所以x+y=4。
点评:本题考查复数的运算及性质,基础题。
题型10:框图
例10.(1)方案1:派出调研人员赴北京、上海、广州调研,待调研人员回来后决定生产数量;
方案2:商家如战场!抓紧时间搞好调研,然后进行生产,调研为此项目的的瓶颈,因此需要添加力量,齐头并进搞调研,以便提前结束调研,尽早投产使产品占领市场.
(2)公司人事结构图
解析:(1)方案1:派出调研人员赴北京、上海、广州调研,待调研人员回来后决定生产数量。

方案2: 商家如战场!抓紧时间搞好调研,然后进行生产,调研为此项目的的瓶颈,因此需要添加力量,齐头并进搞调研,以便提前结束调研,尽早投产使产品占领市场。
于是:

(2)
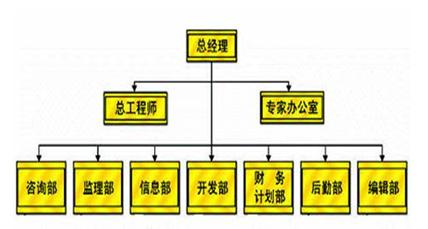
点评:建立合理的结构图和流程图解决实际问题,要形成良好的书写习惯遵循从上到下、从左到右的规则。
4.框图
(1)结构图
首先,你要对所画结构图的每一部分有一个深刻的理解和透彻的掌握,从头止尾抓住主要脉络进行分解,然后将每一步分解进行归纳与提炼,形成一个个知识点并将其逐一地写在矩形框内。最后,按其内在的逻辑顺序将它们排列起来并用线段相连,这样就画成了知识结构图。
认识结构图:由构成系统的若干要素和表达各要素之间关系的连线构成。
绘制结构图的步骤:1)先确定组成系统的基本要素,以及这些要素之间的关系;2)处理好“上位”与“下位”的关系;“下位”要素比“上位”要素更为具体, “上位”要素比“下位”要素更为抽象。3)再逐步细化各层要素;4)画出结构图,表示整个系统。
(2)流程图
绘制流程图的一般过程:首先,用自然语言描述流程步骤;其次,分析每一步骤是否可以直接表达,或需要借助于逻辑结构来表达;再次,分析各步骤之间的关系;最后,画出流程图表示整个流程。
鉴于用自然语言描述算法所出现的种种弊端,人们开始用流程图来表示算法,这种描述方法既避免了自然语言描述算法的拖沓冗长,又消除了起义性,且能清晰准确地表述该算法的每一步骤,因而深受欢迎。
设计算法解决问题的主要步骤:
第一步、用自然语言描述算法;
算法可以用自然语言来描述,但为了使算法的程序或步骤表达得更为直观,我们更经常地用图形方式来表示它。
第二步、画出程序框图表达算法;
第三步、写出计算机相应的程序并上机实现.
3.数系的扩充与复数的引入
形如a+bi(a,b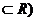 的数,我们把它们叫做复数,全体复数所形成的集合叫做复数集,一般用字母C表示,其中a叫做复数的实部,b叫做复数的虚部。
的数,我们把它们叫做复数,全体复数所形成的集合叫做复数集,一般用字母C表示,其中a叫做复数的实部,b叫做复数的虚部。
复数的加法法则:(a+bi)+(c+di)=(a+c)+(b+d)i;复数的加法法则:(a+bi)-(c+di)=(a-c)+(b-d)i;复数的乘法法则:(a+bi)(c+di)=(ac-bd)+(ad+bc)i;复数的除法法则:(a+bi)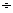 (c+di)=
(c+di)=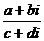

=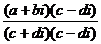

=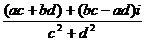

=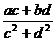 +
+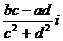 ;
;
(2009浙江卷理)设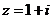 (
(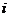 是虚数单位),则
是虚数单位),则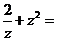 ( )
( )
A.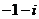 B.
B.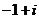 C.
C.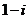 D.
D. 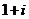
[解析]对于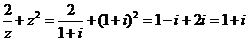
答案 D
(2009金陵中学三模)已知复数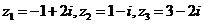 ,它们所对应的点分
,它们所对应的点分
别为A,B,C.若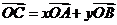 ,则
,则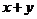 的值是 .
的值是 .
答案 5
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com