
18.(2009辽宁卷理)(本小题满分12分)
某人向一目射击4次,每次击中目标的概率为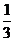 。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
。该目标分为3个不同的部分,第一、二、三部分面积之比为1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。
(Ⅰ)设X表示目标被击中的次数,求X的分布列;
(Ⅱ)若目标被击中2次,A表示事件“第一部分至少被击中1次或第二部分被击中2次”,求P(A) 

解:(Ⅰ)依题意X的分列为. 

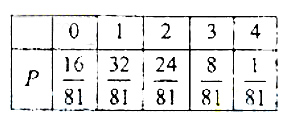
(Ⅱ)设A1表示事件“第一次击中目标时,击中第i部分”,i=1,2.
B1表示事件“第二次击中目标时,击中第i部分”,i=1,2.
依题意知P(A1)=P(B1)=0.1,P(A2)=P(B2)=0.3,
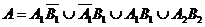 ,
,
所求的概率为
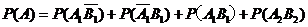
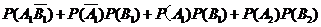
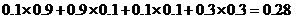 ………12分
………12分
17.(2009全国卷Ⅱ理)(本小题满分12分)
某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核。
(I)求从甲、乙两组各抽取的人数;
(II)求从甲组抽取的工人中恰有1名女工人的概率;
(III)记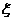 表示抽取的3名工人中男工人数,求
表示抽取的3名工人中男工人数,求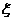 的分布列及数学期望。
的分布列及数学期望。 

分析:(I)这一问较简单,关键是把握题意,理解分层抽样的原理即可。另外要注意此分层抽样与性别无关。
(II)在第一问的基础上,这一问处理起来也并不困难。. 

从甲组抽取的工人中恰有1名女工人的概率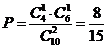
(III)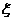 的可能取值为0,1,2,3
的可能取值为0,1,2,3
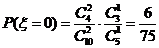 ,
,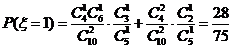 ,
,
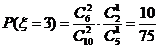 ,
,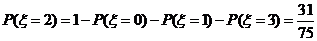
分布列及期望略。
评析:本题较常规,比08年的概率统计题要容易。在计算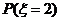 时,采用分类的方法,用直接法也可,但较繁琐,考生应增强灵活变通的能力。
时,采用分类的方法,用直接法也可,但较繁琐,考生应增强灵活变通的能力。
16.(2009四川卷文)(本小题满分12分)
为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡)。某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中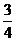 是省外游客,其余是省内游客。在省外游客中有
是省外游客,其余是省内游客。在省外游客中有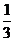 持金卡,在省内游客中有
持金卡,在省内游客中有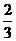 持银卡。
持银卡。

 .
. 

(I)在该团中随机采访2名游客,求恰有1人持银卡的概率;
(II)在该团中随机采访2名游客,求其中持金卡与持银卡人数相等的概率.
[解析]I)由题意得,省外游客有27人,其中9人持金卡;省内游客有9人,其中6人持银卡.
设事件A为“采访该团2人,恰有1人持银卡”,则
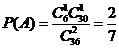
所以采访该团2人,恰有1人持银卡的概率是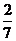 . …………………………………6分
. …………………………………6分
(II)设事件B为“采访该团2人,持金卡人数与持银卡人数相等”,可以分为:
事件B1为“采访该团2人,持金卡0人,持银卡0人”,或事件B2为“采访该团2人,持金卡1人,持银卡1人”两种情况,则
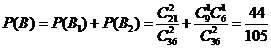
所以采访该团2人,持金卡与持银卡人数相等的概率是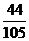 . ……………………12分
. ……………………12分
16.解析:依题意,可分别取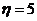 、6、
、6、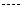 11取,则有
11取,则有
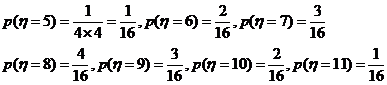 .
. 

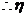 的分布列为
的分布列为
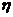 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
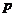 |
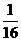 |
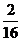 |
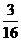 |
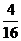 |
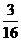 |
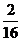 |
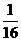 |
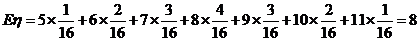 .
.
15.(2009湖北卷理)(本小题满分10分)(注意:在试题卷上作答无效)
一个盒子里装有4张大小形状完全相同的卡片,分别标有数2,3,4,5;另一个盒子也装有4张大小形状完全相同的卡片,分别标有数3,4,5,6。现从一个盒子中任取一张卡片,其上面的数记为x;再从另一盒子里任取一张卡片,其上面的数记为y,记随机变量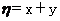 ,求
,求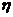 的分布列和数学期望。
的分布列和数学期望。 

14.(2009天津卷文)(本小题满分12分)
为了了解某工厂开展群众体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,用列举法计算这2个工厂中至少有1个来自A区的概率。
[答案](1) 2,3,2(2) 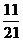
[解析] (1)解: 工厂总数为18+27+18=63,样本容量与总体中的个体数比为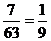 ,所以从A,B,C三个区中应分别抽取的工厂个数为2,3,2.
,所以从A,B,C三个区中应分别抽取的工厂个数为2,3,2.
(2)设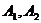 为在A区中抽得的2个工厂,
为在A区中抽得的2个工厂,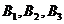 为在B区中抽得的3个工厂,
为在B区中抽得的3个工厂,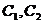 为在C区中抽得的2个工厂,这7个工厂中随机的抽取2个,全部的可能结果有:
为在C区中抽得的2个工厂,这7个工厂中随机的抽取2个,全部的可能结果有: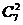 种,随机的抽取的2个工厂至少有一个来自A区的结果有
种,随机的抽取的2个工厂至少有一个来自A区的结果有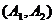 ,
,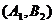
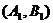
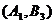
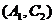
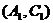 ,同理
,同理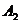 还能组合5种,一共有11种。所以所求的概率为
还能组合5种,一共有11种。所以所求的概率为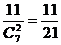
[考点定位]本小题主要考查分层抽样、用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识,考查运用统计、概率知识解决实际问题的能力。
13.(2009江西卷理)(本小题满分12分)
某公司拟资助三位大学生自主创业,现聘请两位专家,独立地对每位大学生的创业方案进行评审.假设评审结果为“支持”或“不支持”的概率都是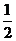 .若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令
.若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令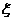 表示该公司的资助总额.
表示该公司的资助总额.
(1) 写出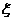 的分布列; (2) 求数学期望
的分布列; (2) 求数学期望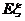 .
.


解:(1)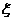 的所有取值为
的所有取值为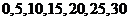
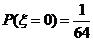
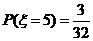
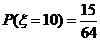
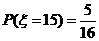
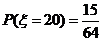
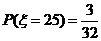
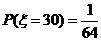
(2)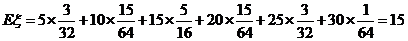 .
.
12.(2009江西卷文)(本小题满分12分)
某公司拟资助三位大学生自主创业,现聘请两位专家,独立地对每位大学生的创业方案进行评审.假设评审结果为“支持”或“不支持”的概率都是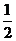 .若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助.求:
.若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助.求:
(1) 该公司的资助总额为零的概率;
(2)该公司的资助总额超过15万元的概率.. 

解:(1)设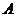 表示资助总额为零这个事件,则
表示资助总额为零这个事件,则
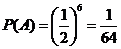
(2)设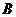 表示资助总额超过15万元这个事件,则
表示资助总额超过15万元这个事件,则
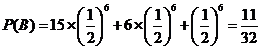
11.(2009安徽卷文)(本小题满分12分)
某良种培育基地正在培育一种小麦新品种A,将其与原有的一个优良品种B进行对照
试验,两种小麦各种植了25亩,所得亩产数据(单位:千克)如下:. 

品种A:357,359,367,368,375,388,392,399,400,405,414,
415,421,423,423,427,430,430,434,443,445,451,454
品种B:363,371,374,383,385,386,391,392,394,395,397
397,400,401,401,403,406,407,410,412,415,416,422,430
(Ⅰ)完成所附的茎叶图
(Ⅱ)用茎叶图处理现有的数据,有什么优点?. 

(Ⅲ)通过观察茎叶图,对品种A与B的亩产量及其稳定性进行比较,写出统计结论。
[思路]由统计知识可求出A、B两种品种的小麦稳定性大小并画出茎叶图,用茎叶图处理数据,看其分布就比较明了。. 

[解析](1)茎叶图如图所示
|
A |
|
B |
|
9 7 |
35 |
|
|
8 7 |
36 |
3 |
|
5 |
37 |
1 4 |
|
8 |
38 |
3 5 6 |
|
9 2 |
39 |
1 2 4 457 7 |
|
5 0 |
40 |
0 1 1 3 6 7 |
|
5 4 2 |
41 |
0 2 5 6 |
|
7 3 3 1 |
42 |
2 |
|
4 0 0 |
43 |
0 |
|
5 5 3 |
44 |
|
|
4 1 |
45 |
|
(2)用茎叶图处理现有的数据不仅可以看出数据的分布状况,而且可以看出每组中的具体数据.
(3)通过观察茎叶图,可以发现品种A的平均每亩产量为411.1千克,品种B的平均亩产量为397.8千克.由此可知,品种A的平均亩产量比品种B的平均亩产量高.但品种A的亩产量不够稳定,而品种B的亩产量比较集中D平均产量附近.
10.(2009安徽卷理)(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区.B肯定是受A感染的.对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是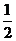 .同样也假定D受A、B和C感染的概率都是
.同样也假定D受A、B和C感染的概率都是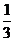 .在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量.写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
.在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量.写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
本小题主要考查古典概型及其概率计算,考查取有限个值的离散型随机变量及其分布列和均值的概念,通过设置密切贴近现实生活的情境,考查概率思想的应用意识和创新意识。体现数学的科学价值。本小题满分12分。
解:随机变量X的分布列是
|
X |
1 |
2 |
3 |
|
P |
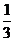 |
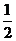 |
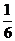 |
X的均值为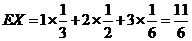
附:X的分布列的一种求法
共有如下6种不同的可能情形,每种情形发生的概率都是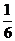 :
:
|
① |
② |
③ |
④ |
⑤ |
⑥ |
|
A-B-C-D |
A-B-C └D |
A-B-C └D |
A-B-D └C |
A-C-D └B |
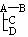 |
在情形①和②之下,A直接感染了一个人;在情形③、④、⑤之下,A直接感染了两个人;在情形⑥之下,A直接感染了三个人。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com