
7、(上海)7.某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量 表示选出的志愿者中女生的人数,则数学期望
表示选出的志愿者中女生的人数,则数学期望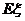 ____________(结果用最简分数表示).
____________(结果用最简分数表示).
6、(湖南卷) 13、一个总体分为A,B两层,其个体数之比为4:1,用分层抽样方法从总体中抽取一个容量为10的样本,已知B层中甲、乙都被抽到的概率为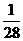 ,则总体中的个数数位
。
,则总体中的个数数位
。
[答案]:40
5、(广东卷) 12.已知离散型随机变量
12.已知离散型随机变量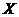 的分布列如右表.若
的分布列如右表.若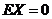 ,
,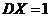 ,则
,则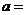 ,
,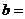 .
.
[解析]由题知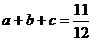 ,
,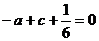 ,
,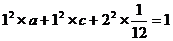 ,解得
,解得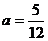 ,
,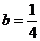 .
.
8.[答案]:B
4、(福建卷)8.已知某运动员每次投篮命中的概率都为40%。现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,
指定1,2,3,4表示命中,5,6,,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果。经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为
A.0.35 B 0.25 C 0.20 D 0.15
3、(安徽卷理)(10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于高.考.资.源.网
(A)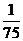 (B)
(B) 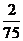 (C)
(C)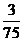 (D)
(D)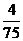
 [解析] 如图,甲从这6个点中任意选两个点连成直线,乙也从这
[解析] 如图,甲从这6个点中任意选两个点连成直线,乙也从这
6个点中任意选两个点连成直线,共有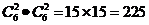
种不同取法,其中所得的两条直线相互平行但不重合有
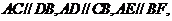
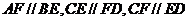


共12对,所以所求概率为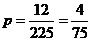 ,选D
,选D
2、(江苏卷)5.现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m的概率为 ▲ .
[解析] 考查等可能事件的概率知识。 
所求概率为0.2。
3.[答案]C
1、(湖北卷理) 3、投掷两颗骰子,得到其向上的点数分别为m和n,则复数(m+ni)(n-mi)为实数的概率为
A、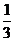 B、
B、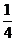
C、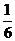 D、
D、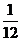
15.观察下列等式:
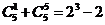 ,
,
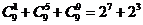 ,
,
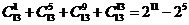 ,
,
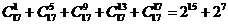 ,
,
………
由以上等式推测到一个一般的结论:
对于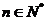 ,
,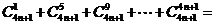 .
. 

答案: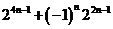
[解析]这是一种需类比推理方法破解的问题,结论由二项构成,第二项前有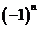 ,二项指数分别为
,二项指数分别为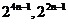 ,因此对于
,因此对于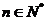 ,
,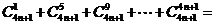
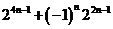
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com