
21、证明: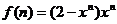 ,
,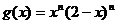 ,比较
,比较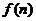 与
与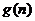 的大小,即比较
的大小,即比较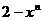 与
与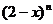 的大小。 猜想:
的大小。 猜想: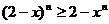 (当且仅当
(当且仅当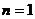 时,等号成立)
时,等号成立)
下面用数学归纳法加以证明:
(1)当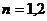 时,易证。(略)
时,易证。(略)
(2)假设当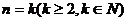 时,猜想成立,即
时,猜想成立,即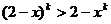
当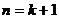 时,
时,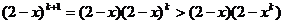 (注:
(注: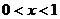 )
)
要证猜想成立,只需证明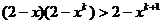 即证
即证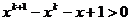 亦即
亦即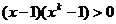 由
由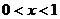 易得上式成立,即
易得上式成立,即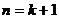 时,猜想成立。 综上(1)(2)可知,猜想成立。 (另证:令
时,猜想成立。 综上(1)(2)可知,猜想成立。 (另证:令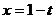 ,要证
,要证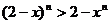 ,即证
,即证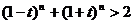 ,由二项式定理展开,易得证。)
,由二项式定理展开,易得证。)
20、解:(1)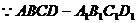 是直四棱柱,
是直四棱柱,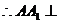 面
面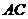 ,又
,又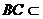 面
面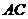 ,所以
,所以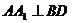 。 又
。 又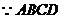 是菱形,
是菱形,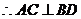 ,所以
,所以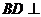 面
面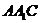 。
。
即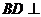 面
面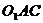 ,又
,又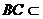 面
面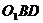 ,所以平面
,所以平面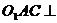 平面
平面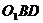 。
。
(2)过O作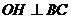 于H,连接
于H,连接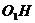 ,则
,则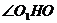 为二面角
为二面角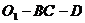 的平面角。
的平面角。
在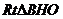 中,
中,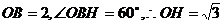 。 又
。 又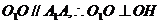 。
。
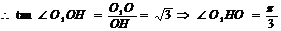 。故二面角
。故二面角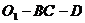 的大小为
的大小为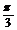 。
。
19、解:(1)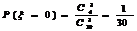 ;
; 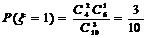 ;
;
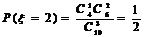 ;
; 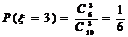 。
。
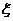 |
0 |
1 |
2 |
3 |
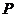 |
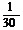 |
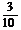 |
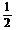 |
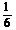 |
所以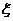 的分布列为
的分布列为
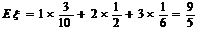 。
。
(2)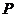 (甲合格)=
(甲合格)=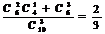 ;
; 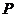 (乙合格)=
(乙合格)=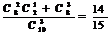 ;
;
所求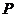 =
=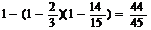 。
。
18.(1)2,(2)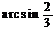
17.解:(1)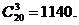 (2)由
(2)由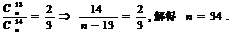
(3)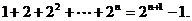 (4)
(4)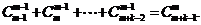 证明:
证明:
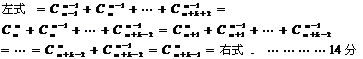
16、解:(1)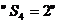 即前四次中有三次出现“√”,一次出现“×”,
即前四次中有三次出现“√”,一次出现“×”,
所以概率为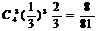 。
。
2)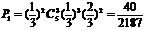 ,
,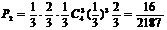 所求概率为
所求概率为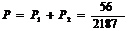 。
。
21.设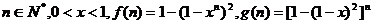 ,试比较
,试比较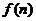 与
与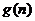 的大小,并证明你的结论.
的大小,并证明你的结论.
解答:
20.如图,直四棱柱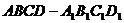 的高为3,底面是边长为4的菱形
,且
的高为3,底面是边长为4的菱形
,且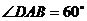 ,
,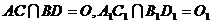 ,
,
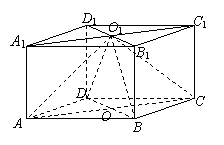 (1)求证:平面
(1)求证:平面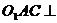 平面
平面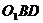 ;
;
(2)求二面角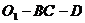 的大小.
的大小.
19.甲、乙两人参加一次英语口语考试,已知在编号为1-10的10道试题中,甲能答对编号为1-6的6道题,乙能答对编号为3-10的8道题,规定每位考生都从备选题中抽出3道试题进行测试,至少答对2道才算合格,(1)求甲答对试题数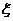 的概率分布及数学期望;
的概率分布及数学期望;
(2)求甲、乙两人至少有一人考试合格的概率.
18.在长方体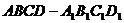 中,
中,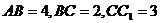 ,
,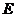 分
分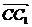 所成比为2,
所成比为2,
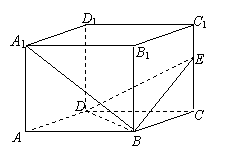 (1)求点
(1)求点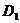 到平面
到平面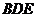 的距离;
的距离;
(2)求直线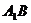 与平面
与平面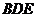 所成角的大小.
所成角的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com