1．(2009·重庆高考)在如图1所示的电路中，电池均相同，当电键S分别置于a、b两处时，导线MM′与NN′之间的安培力的大小分别为F_a、F_b，可判断这两段导线(　)

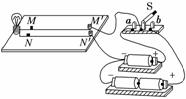
图1

A．相互吸引，F_a＞F_b　　　　　　　 B．相互排斥，F_a＞F_b

C．相互吸引，F_a＜F_b 　　　　　　　　D．相互排斥，F_a＜F_b

解析：无论电键置于a还是置于b，两导线中通过的都是反向电流，相互间作用力为斥力，A、C错误．电键置于位置b时电路中电流较大，导线间相互作用力也较大，故C错误，D正确．

答案：D

16．(17分)(2009·江苏高考)1932年，劳伦斯和利文斯顿设计出了回旋加速器．回旋加速器的工作原理如图17所示，置于高真空中的D形金属盒半径为R，两盒间的狭缝很小，带电粒子穿过的时间可以忽略不计，磁感应强度为B的匀强磁场与盒面垂直，A处粒子源产生的粒子，质量为m，电荷量为+q，在加速器中被加速，加速电压为U.加速过程中不考虑相对论效应和重力作用．

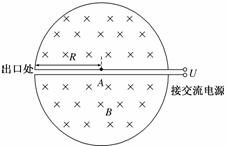
图17

(1)求粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比；

(2)求粒子从静止开始加速到出口处所需的时间t；

(3)实际使用中，磁感应强度和加速电场频率都有最大值的限制．若某一加速器磁感应

强度和加速电场频率的最大值分别为B_m、f_m，试讨论粒子能获得的最大动能E_km.

解析：(1)设粒子第1次经过狭缝后的半径为r₁，速度为v₁

qU＝mv₁²

qv₁B＝m

解得r₁＝

同理，粒子第2次经过狭缝后的半径r₂＝

则r₂∶r₁＝∶1.

(2)设粒子到出口处时被加速了n圈

2nqU＝mv²

qvB＝m

T＝

t＝nT

解得t＝.

(3)加速电场的频率应等于粒子在磁场中做圆周运动的频率，即f＝

当磁感应强度为B_m时，加速电场的频率为f_Bm＝

粒子的动能E_k＝mv²

当f_Bm≤f_m时，粒子的最大动能由B_m决定

qv_mB_m＝m

解得E_km＝

当f_Bm≥f_m时，粒子的最大动能由f_m决定

v_m＝2πf_mR

解得E_km＝2π²mf_m²R².

答案：(1)∶1　(2)　(3)见解析

15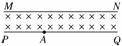．(14分)一质量为m、电荷量为q的带负电的带电粒子，从A点射入宽度为d、磁感应强度为B的匀强磁场，MN、PQ为该磁场的边界线，磁感线垂直于纸面向里，磁场区域足够长．如图16所示．带电粒子射入时的初速度与PQ成45°角，且粒子恰好没有从MN射出．(不计粒子所受重力)求：

(1)该带电粒子的初速度v₀；　　　　　　　　　　　　　　　　　　　　　 图16

(2)该带电粒子从PQ边界射出的射出点到A点的距离x.

解析：(1)若初速度向右上方，设轨道半径为R₁，如图甲所示．

则R₁＝(R₁－d)/cos45°，

R₁＝(2+)d.

又R₁＝，解得v₀＝.

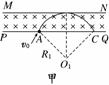
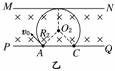
若初速度向左上方，设轨道半径为R₂，如图乙所示．

则(d－R₂)/cos45°＝R₂，

R₂＝(2－)d，v₀＝.

(2)若初速度向右上方，设射出点C到A点的距离为x₁，

则x₁＝R₁＝2(+1)d.

若初速度向左上方，设射出点到A点的距离为x₂，

则x₂＝R₂＝2(－1)d.

答案：见解析

14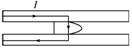．(12分)据报道，最近已研制出一种可以投入使用的电磁轨道炮，其原理如图15所示．炮弹(可视为长方形导体)置于两固定的平行导轨之间，并与轨道壁密接．开始时炮弹在导轨的一端，通电流后，炮弹会被磁场力加速，最后从位于导轨另一端的出口高速射出．设两导轨之间的距离d＝0.10 m，导轨长 L＝5.0 m，炮弹质量m＝0.30 kg.导轨上的电流I的方向如图中箭头所示．可认为，炮弹在轨道内运动时，它所在处磁场的磁感应强度始终为B＝2.0 T，方向垂直于纸面向里．若炮弹出口速度为 v＝2.0×10³ m/s，求通过导轨的电流I.(忽略摩擦力与重力的影响)

解析：当导轨通有电流I时，炮弹作为导体受到磁场施加的安培力为　 图 15

F＝IdB　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　①

设炮弹加速度的大小为a，则有

F＝ma　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

炮弹在两导轨间做匀加速运动，因而

v²＝2aL　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③

联立①②③式得

I＝

代入题给数据得I＝6.0×10⁵ A.

答案：6.0×10⁵ A

13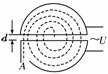．(12分)如图14所示，回旋加速器D形盒的半径为R，用来加速质量为m、电荷量为q

的质子，使质子由静止加速到能量为E后，由A孔射出，求：

(1)加速器中匀强磁场B的方向和大小；

(2)设两D形盒间距为d，其间电压为U，电场视为匀强电场，质子每次经电

场加速后能量增加，加速到上述能量所需回旋周数；

(3)加速到上述能量所需时间．

解析：(1)带电粒子在磁场中做匀圆周运动，由Bqv＝得，v＝，又E＝mv²＝

m()²，

所以B＝，方向垂直于纸面向里．

(2)带电粒子每经过一个周期被电场加速二次，能量增加2qU，则：E＝2qUn，n＝.

(3)可以忽略带电粒子在电场中运动的时间，又带电粒子在磁场中运行周期T＝，所

以

t_总＝nT＝×＝＝.

答案：(1)　方向垂直于纸面向里

(2)　(3)

12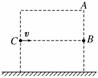．带电粒子以速度v沿CB方向射入一横截面为正方形的区域．C、B均为该正方形两边

的中点，如图13所示，不计粒子的重力．当区域内有竖直方向的匀强电场E时，粒子

从A点飞出，所用时间为t₁；当区域内有垂直于纸面向里的磁感应强度为

B的匀强磁场时，粒子也从A点飞出，所用时间为t₂，下列说法正确的是

(　)

A．t₁<t₂　 　　　　　　　B．t₁>t₂ 图13

C.＝v　 　　　　　　　D.＝v

解析：带电粒子在匀强电场中做类平抛运动，水平方向上做匀速运动，而在匀强磁场中做匀速圆周运动，水平方向上做减速运动，所以t₂>t₁，A项正确，B项错；设正方形区域的边长为l，则当加电场时，有l＝vt₁和＝t₁²，得E＝.当加磁场时，根据几何关系，有(R－)²+l²＝R²，得R＝l，再由R＝得B＝.所以＝v，D项对，C项错．

答案：AD

11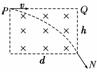．一电子以与磁场垂直的速度v从P处沿PQ方向进入长为d、宽为h的匀强磁场区域，从N点射出，如图12所示，若电子质量为m，电荷量为e，磁感应强度为B，则　　　　　　　　　　　　　　　　 ( 　)

A．h＝d

B．电子在磁场中运动的时间为

C．电子在磁场中运动的时间为

D．洛伦兹力对电子不做功

解析：过P点和N点作速度的垂线，两垂线的交点即为电子在磁场中做匀速圆周运动时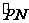的圆心O，由勾股定理可得(R－h)²+d²＝R²，整理知d＝，而R＝，故d＝，所以A错误．由带电粒子在有界磁场中做匀速圆周运动，得t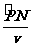＝，故B错误，C正确．又由于洛伦兹力和粒子运动的速度总垂直，对粒子永远也不做功，故D正确．

答案：CD

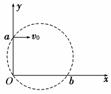
10．(2010·徐州模拟)如图11所示，在平面直角坐标系中有一个垂直于纸面向里的圆形匀强磁场，其边界过原点O和y轴上的点a(0，L)．一质量为m、电荷量为e的电子从a点以初速度v₀平行于x轴正方向射入磁场，并从x轴上的b点射出磁场，此时速度方向与x轴正方向的夹角为60°.下列说法中正确的是　　　　　　　　　　　　　　　　　 (　) 　图11

A．电子在磁场中运动的时间为

B．电子在磁场中运动的时间为

C．磁场区域的圆心坐标(，)

D．电子在磁场中做圆周运动的圆心坐标为(0，－2L)

解析：由图可以计算出电子做圆周运动的半径为2L，故在磁场中运动的时间为t＝

＝，A错，B正确；ab是磁场区域圆的直径，故圆心坐标为(L，)，电子在磁

场中做圆周运动的圆心为O′，计算出其坐标为(0，－L)，所以C正确，D错误．

答案：BC

9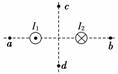．两根通电的长直导线平行放置，电流分别为I₁和I₂，电流的方向如图10所示，在与导线垂直的平面上有a、b、c、d四点，其中a、b在导线横截面连线的延长线上，c、d在导线横截面连线的垂直平分线上．则导线中的电流在这四点产生的磁场的磁感应强度可能为零的是(　)

A．a点　　　　　B．b点　　　　　　　　　　　　　　　　　　　 图10

C．c点　 　　　　　　　　D．d点

解析：由安培定则可知，直线电流的磁场是以导线为圆心的同心圆，I₁产生的磁场方向为逆时针方向，I₂产生的磁场方向为顺时针方向，则I₁在a点产生的磁场竖直向下，I₂在a点产生的磁场竖直向上，在a点磁感应强度可能为零，此时需满足I₂>I₁；同理，在b点磁感应强度也可能为零，此时需满足I₁>I₂.I₁在c点产生的磁场斜向左上方，I₂在c点产生的磁场斜向右上方，则c点的磁感应强度不可能为零，同理，在d点的磁感应强度也不可能为零，故选项A、B正确．

答案：AB

8．(2008·广东高考)带电粒子进入云室会使云室中的气体电离，从而显示

其运动轨迹．图9所示是在有匀强磁场的云室中观察到的粒子的轨迹，

a和b是轨迹上的两点，匀强磁场B垂直于纸面向里．该粒子在运动

时，其质量和电荷量不变，而动能逐渐减少，下列说法正确的是(　)

A．粒子先经过a点，再经过b点　　　　　　　　　　　　　　　　　　　　 图 9

B．粒子先经过b点，再经过a点

C．粒子带负电

D．粒子带正电

解析：由于粒子的速度减小，所以轨道半径不断减小，所以A对B错；由左手定则得粒子应带负电，C对D错．

答案：AC