
2. 若条件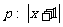 ≤4,条件
≤4,条件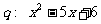 ≤
≤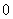 ,则
,则 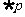 是
是 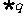 的
的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
1. 集合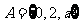 ,
,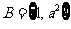 ,若
,若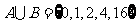 ,则
,则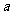 的值为
的值为
A.0 B.1 C.2 D.4
例1(课本第82页
例2)用计算机作出的图像,并在同一坐标系下作出下列函数的图象,并指出它们与指数函数y=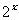 的图象的关系,
的图象的关系,
⑴y=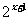 与y=
与y=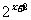 .
⑵y=
.
⑵y=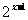 与y=
与y=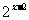 .
.
解:⑴作出图像,显示出函数数据表
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
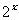 |
0.125 |
0.25 |
0.5 |
1 |
2 |
4 |
8 |
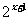 |
0.25 |
0.5 |
1 |
2 |
4 |
8 |
16 |
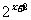 |
0.5 |
1 |
2 |
4 |
8 |
16 |
32 |
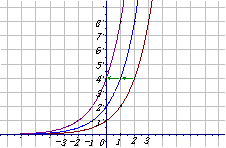 比较函数y=
比较函数y=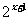 、y=
、y=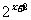 与y=
与y=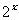 的关系:将指数函数y=
的关系:将指数函数y=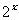 的图象向左平行移动1个单位长度,就得到函数y=
的图象向左平行移动1个单位长度,就得到函数y=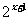 的图象,将指数函数y=
的图象,将指数函数y=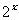 的图象向左平行移动2个单位长度,就得到函数y=
的图象向左平行移动2个单位长度,就得到函数y=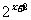 的图象
的图象
⑵作出图像,显示出函数数据表
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
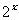 |
0.125 |
0.25 |
0.5 |
1 |
2 |
4 |
8 |
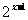 |
0.625 |
0.125 |
0.25 |
0.5 |
1 |
2 |
4 |
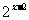 |
0.3125 |
0.625 |
0.125 |
0.25 |
0.5 |
1 |
2 |
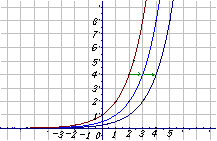 比较函数y=
比较函数y=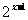 、y=
、y=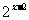 与y=
与y=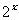 的关系:将指数函数y=
的关系:将指数函数y=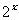 的图象向右平行移动1个单位长度,就得到函数y=
的图象向右平行移动1个单位长度,就得到函数y=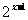 的图象,将指数函数y=
的图象,将指数函数y=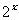 的图象向右平行移动2个单位长度,就得到函数y=
的图象向右平行移动2个单位长度,就得到函数y=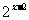 的图象
的图象
小结:⑴
y=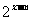 与y=
与y=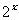 的关系:当m>0时,将指数函数y=
的关系:当m>0时,将指数函数y=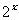 的图象向右平行移动m个单位长度,就得到函数y=
的图象向右平行移动m个单位长度,就得到函数y=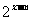 的图象;当m<0时,将指数函数y=
的图象;当m<0时,将指数函数y=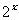 的图象向左平行移动m个单位长度,就得到函数y=
的图象向左平行移动m个单位长度,就得到函数y=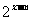 的图象
的图象
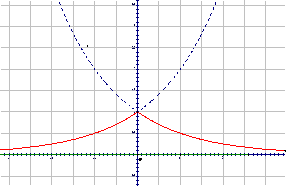 例2 ⑴已知函数
例2 ⑴已知函数
 用计算器或计算机作出函数图像,求定义域、值域,并探讨
用计算器或计算机作出函数图像,求定义域、值域,并探讨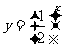 与
与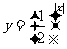 图像的关系
图像的关系
解: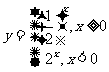 定义域:xÎR 值域:
定义域:xÎR 值域:
关系:将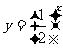 的图像y轴右侧的部分翻折到y轴左侧的到
的图像y轴右侧的部分翻折到y轴左侧的到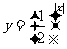 的图像,关于y轴对称.
的图像,关于y轴对称.
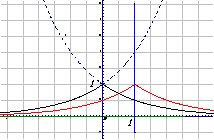 ⑵已知函数
⑵已知函数
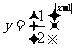 用计算器或计算机作出函数图像,求定义域、值域,并探讨
用计算器或计算机作出函数图像,求定义域、值域,并探讨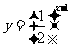 与
与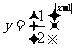 图像的关系
图像的关系
解: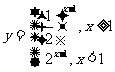 定义域:xÎR 值域:
定义域:xÎR 值域: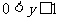
关系:将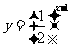 (x>1)的图像在直线x=1右侧的部分翻折到直线x=1左侧得到
(x>1)的图像在直线x=1右侧的部分翻折到直线x=1左侧得到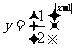 的图像,是关于直线x=1对称
的图像,是关于直线x=1对称
⑵推广:对于有些复合函数的图象,则常用基本函数图象+变换方法作出:
基本函数图象+变换:即把我们熟知的基本函数图象,通过平移、作其对称图等方法,得到我们所要求作的复合函数的图象,如上例,这种方法我们遇到的有以下几种形式:
|
函
数 |
y=f(x) |
|
y=f(x+a) |
a>0时,向左平移a个单位;a<0时,向右平移|a|个单位. |
|
y=f(x)+a |
a>0时,向上平移a个单位;a<0时,向下平移|a|个单位. |
|
y=f(-x) |
y=f(-x)与y=f(x)的图象关于y轴对称. |
|
y=-f(x) |
y=-f(x)与y=f(x)的图象关于x轴对称. |
|
y=-f(-x) |
y=-f(-x)与y=f(x)的图象关于原点轴对称. |
|
y=f(|x|) |
y=f(|x|)的图象关于y轴对称,x 0时函数即y=f(x),所以x<0时的图象与x 0时函数即y=f(x),所以x<0时的图象与x 0时y=f(x)的图象关于y轴对称. 0时y=f(x)的图象关于y轴对称. |
|
y=|f(x)| |
∵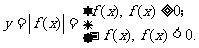 ,∴y=|f(x)|的图象是y=f(x) ,∴y=|f(x)|的图象是y=f(x) 0与y=f(x)<0图象的组合. 0与y=f(x)<0图象的组合. |
y=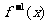 |
y=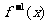 与y=f(x)的图象关于直线y=x对称. 与y=f(x)的图象关于直线y=x对称. |
以上是在高一阶段我们看到的几种函数图象的变换,但随着知识的增加,还会有许多较复杂的变换,以后再作研究.
例3探讨函数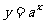 和
和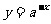
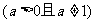 的图象的关系,并证明关
的图象的关系,并证明关
于y轴对称
证:设P(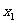 ,
,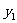 )是函数
)是函数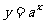
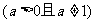 的图象上任意一点
的图象上任意一点
则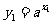 而P(
而P(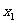 ,
,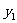 )关于y轴的对称点Q是(-
)关于y轴的对称点Q是(-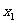 ,
,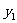 )
)
∴ 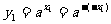 即Q在函数
即Q在函数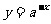 的图象上
的图象上
由于P是任意取的,所以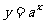 上任一点关于y轴的对称点都在
上任一点关于y轴的对称点都在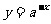 的图象上
的图象上
同理可证: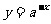 图象上任意一点也一定在函数
图象上任意一点也一定在函数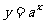 的图象上
的图象上
∴ 函数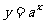 和
和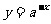 的图象关于y轴对称
的图象关于y轴对称
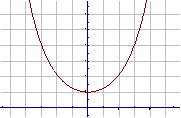 例4 已知函数
例4 已知函数 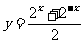 求函数的定义域、值域
求函数的定义域、值域
解:作出函数图像,观察分析讨论,教师引导、整理
定义域为
R
由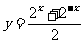 得
得 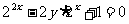
∵xÎR, ∴△ 0, 即
0, 即 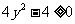 , ∴
, ∴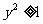 , 又∵
, 又∵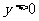 ,∴
,∴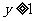
20. (本小题满分14分)
已知向量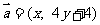 , 向量
, 向量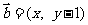 , 且
, 且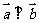 , 动点
, 动点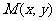 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程;
(2)证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B, 且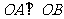 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
高级中学2010-2011学年第一学期高三第一次测试
19.(本小题满分14分)
如图,过抛物线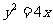 上一点P(
上一点P(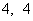 ),作两条直线分别交抛物线于A(
),作两条直线分别交抛物线于A(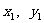 ),B(
),B(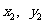 ).
).
直线PA与PB的斜率存在且互为相反数,(1)求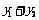 的值,(2)证明直线AB的斜率是非零常数.
的值,(2)证明直线AB的斜率是非零常数.
18. (本小题满分14分)
已知动圆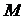 经过点
经过点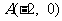 ,且与圆
,且与圆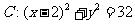 内切.
内切.
(1)求动圆圆心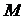 的轨迹
的轨迹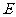 的方程;(2)求轨迹E上任意一点
的方程;(2)求轨迹E上任意一点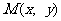 到定点B(1,0)的距离
到定点B(1,0)的距离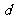 的最小值,并求
的最小值,并求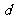 取得最小值时的点M的坐标.
取得最小值时的点M的坐标.
17. (本小题满分14分)
(1)掷两颗骰子,其点数之和为4的概率是多少?
(2)甲、乙两人约定上午9点至12点在某地点见面,并约定任何一个人先到之后等另一个人不超过一个小时,一小时之内如对方不来,则离去。如果他们二人在8点到12点之间的任何时刻到达约定地点的概率都是相等的,求他们见到面的概率。
16.(本小题满分12分)
已知圆经过点A(2,-3)和B(-2,-5).
(1)若圆心在直线x-2y-3=0上,求圆的方程. (2)若圆的面积最小,求圆的方程;
15. (本小题满分12分)
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
|
|
文艺节目 |
新闻节目 |
总计 |
|
20至40岁 |
42 |
16 |
58 |
|
大于40岁 |
18 |
24 |
42 |
|
总计 |
60 |
40 |
100 |
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名观众,大于40岁的观众应该抽取几名?
(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率。
14.设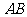 是椭圆
是椭圆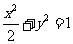 的不垂直于对称轴的弦,
的不垂直于对称轴的弦,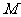 为
为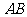 的中点,
的中点,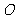 为坐标原点,则
为坐标原点,则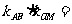 ****
****
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com